Have you ever wondered how priority queues efficiently manage tasks in your computer’s operating system? Or how a database quickly retrieves the maximum or minimum record from a large dataset? The secret behind these operations is a fascinating data structure known as a heap.

Heaps, despite their somewhat unglamorous name, are incredibly powerful and versatile. They are the unsung heroes that quietly power many of the systems and algorithms we use daily. But what exactly is a heap? How does it work, and why is it so efficient?

In this blog post, we’ll answer these intriguing questions and more. We’ll start from the basics, delve into the different types of heaps, and explore their real-world applications. Whether you’re a seasoned programmer or a beginner, this guide will provide you with a thorough understanding of heaps.

So, are you ready to uncover the mysteries of heap data structures and learn how they can make your code more efficient? Let’s embark on this exciting journey together!

Before moving to directly heap let’s first understand a little about tree data structure because heap is a specialized tree-based data structure.

Tree Data Structure:

It simulates a hierarchical tree structure, with a set of connected nodes. It’s a non-linear data structure compared to arrays, linked lists, stacks, and queues which are linear data structures.

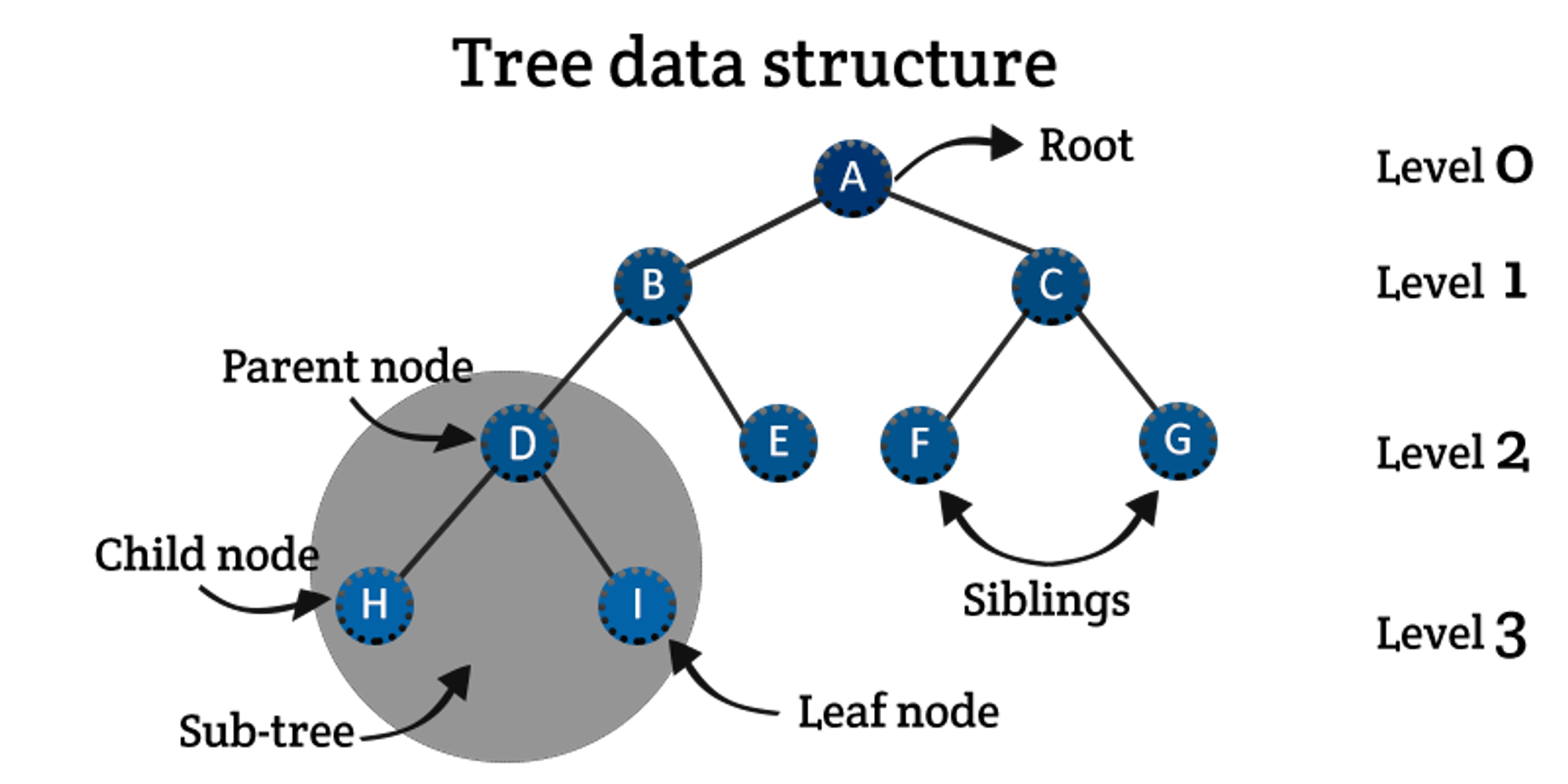
Here are some key points about trees:

A tree is a collection of entities called nodes. Nodes are connected by edges.
Each node contains a value or data, and it may or may not link to other nodes.
The node at the top of the tree is called the root. If the nodes are connected, there is exactly one path from the root to each node.
The connections from one node to another are called branches, and nodes are also known as children. The originating node is often referred to as the parent node.
Nodes with the same parent are called siblings.
Nodes without children are called leaf nodes or external nodes, while nodes with at least one child are called internal nodes.

Understanding these basics of the tree data structure will make understanding heaps, which are a specific type of binary tree, much easier Let’s now understand binary trees.

Binary Tree:

A Binary Tree is a type of tree data structure in which each node can have at most two children. These are typically referred to as the left child and the right child.

There are also several types of binary trees, we will discuss three of them full binary tree, Almost full binary tree and complete binary trees. All the above three have these two props in common :

Insertion of the node should be from left to right
Upper-level nodes will be filled up before coming to the lower level.

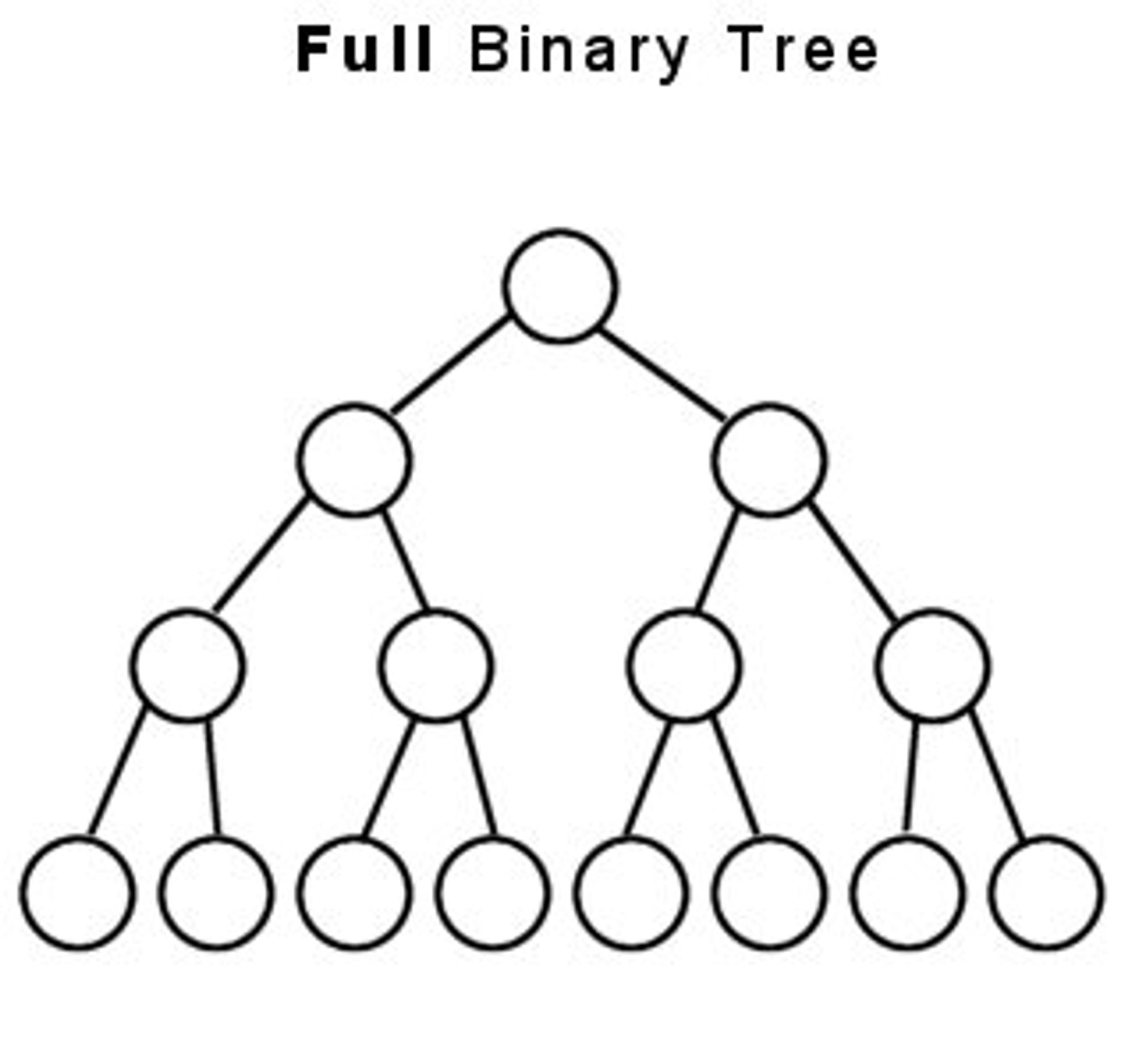
Full Binary Tree: A binary tree in which every node has either two or no children.

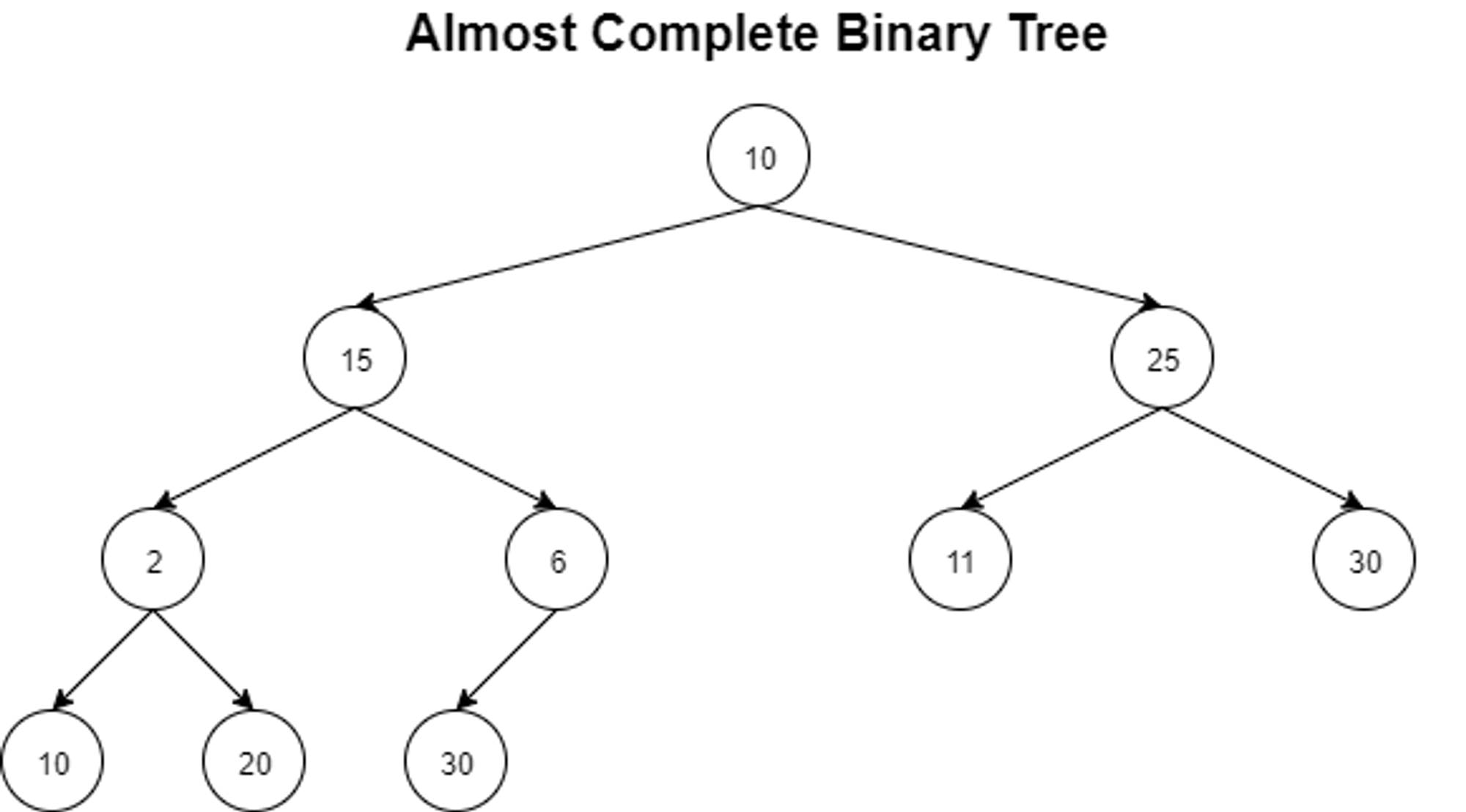
Almost complete Binary Tree: A tree that follows the above two common props but in the last level all children do not have two children.

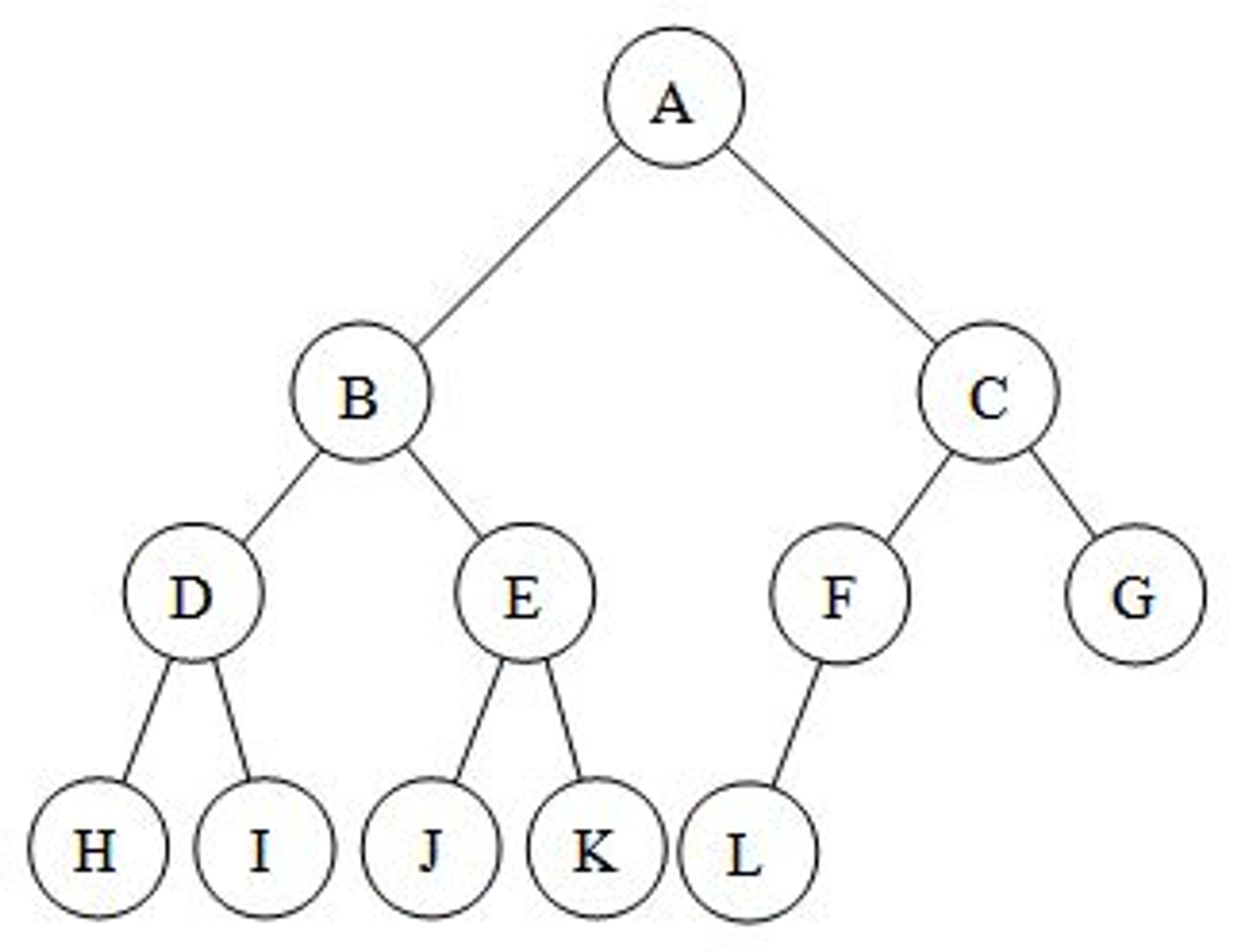
Complete Binary Tree: This is the superset of the above-discussed two trees.

After understanding all of this let's now move to heap.

Heap:

A Heap is a special type of binary tree. It has two additional properties:

Shape Property: A heap must be a complete binary tree, which means all levels of the tree are filled except for possibly the last level, which is filled from left to right.
Heap Property: Each node’s value in a heap must follow a specific order concerning its children’s values. Two types of heaps differ in the way they order the values:
- Max Heap: In a max heap, the value of each node is less than or equal to the value of its parent. This means the maximum value is at the root of the tree. This heap can be used to find the maximum in an array.
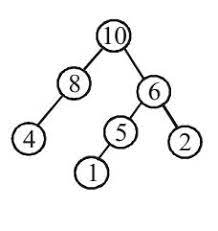
- Min Heap: In a min heap, the value of each node is greater than or equal to the value of its parent. This means the minimum value is at the root of the tree. This heap can be used to find the minimum in an array

Insertion in a heap:

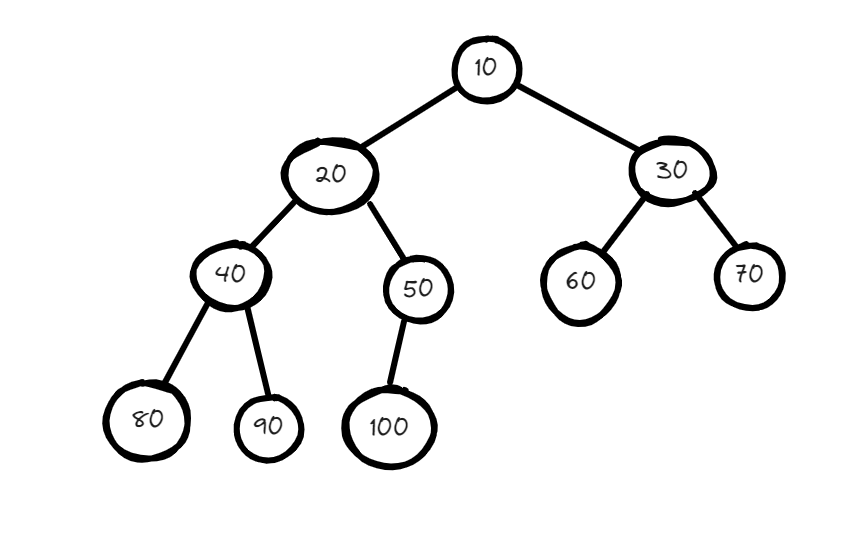
Let's have a minheap that will look something like this :

Now we will try to add a node having value 5 to this min heap. After adding that node our minheap will look something like this :

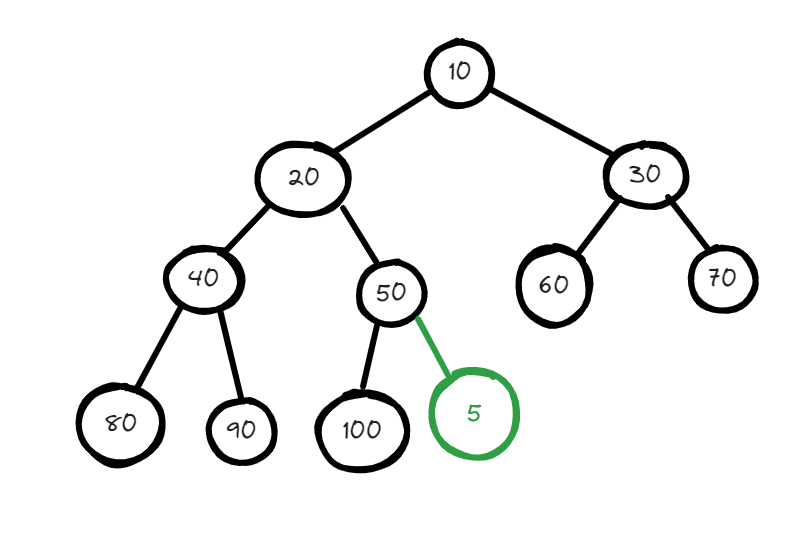
but the question here is this a valid minheap? No, it is not because the parent of the node having value 5 is larger than its children so we have to swap this.

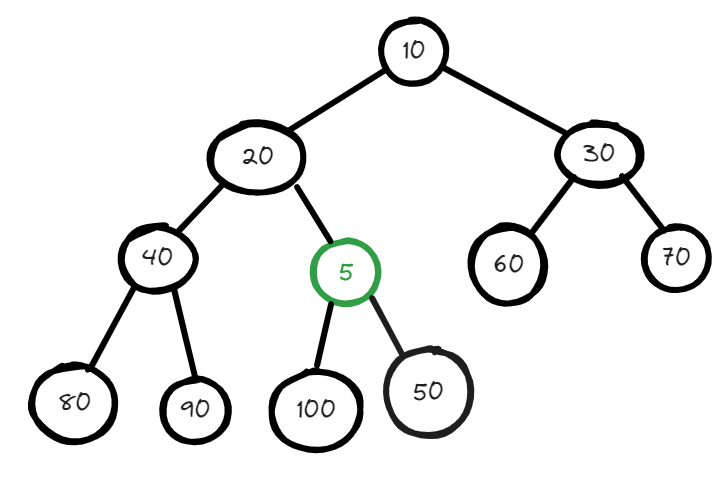
after swap your min heap will look something like this. Is this a valid minheap, no it is not. Let's do some more swaps :

Now we have a valid min heap. Here we have done a total of 3 swaps one 5 and 50, another 20 and 5 and the last 10 and 5. We moved from the bottom to the top of the tree. Can we say that if in any minheap if I will insert a new node then I do the swaps equal to the height of the min tree? The formula for the height of a tree is :

Height = log(n+1)

Where n denotes the number of total nodes in CBT. From here we can say that the total number of swaps will be log(n) so the time complexity for insertion in a minheap will be O(log(n))

Deletion in Heap:

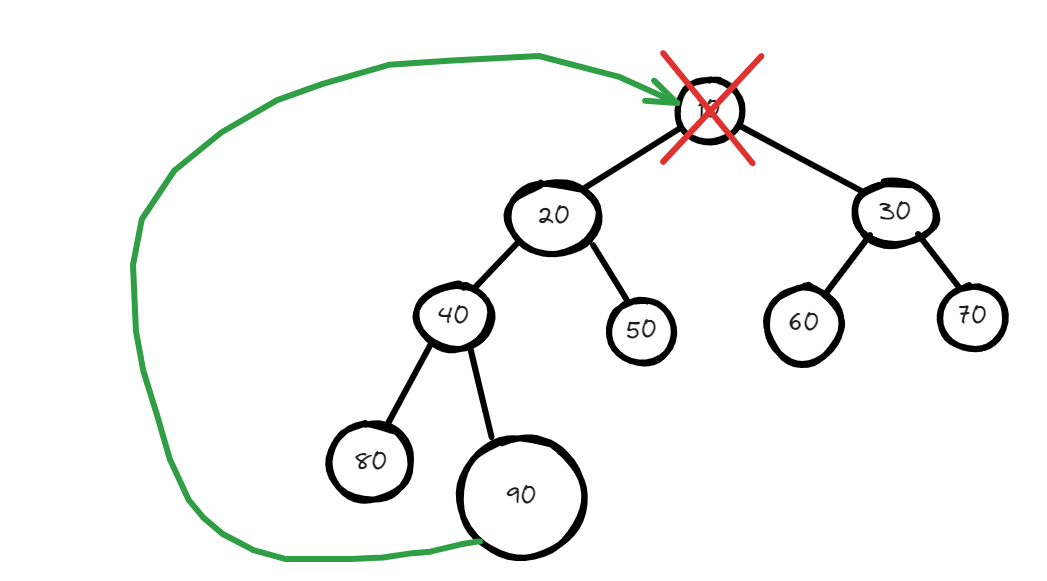
Replace the root with the last element: The standard deletion operation on a heap is to delete the element present at the root node of the heap. This is done by replacing the root with the last element in the heap.
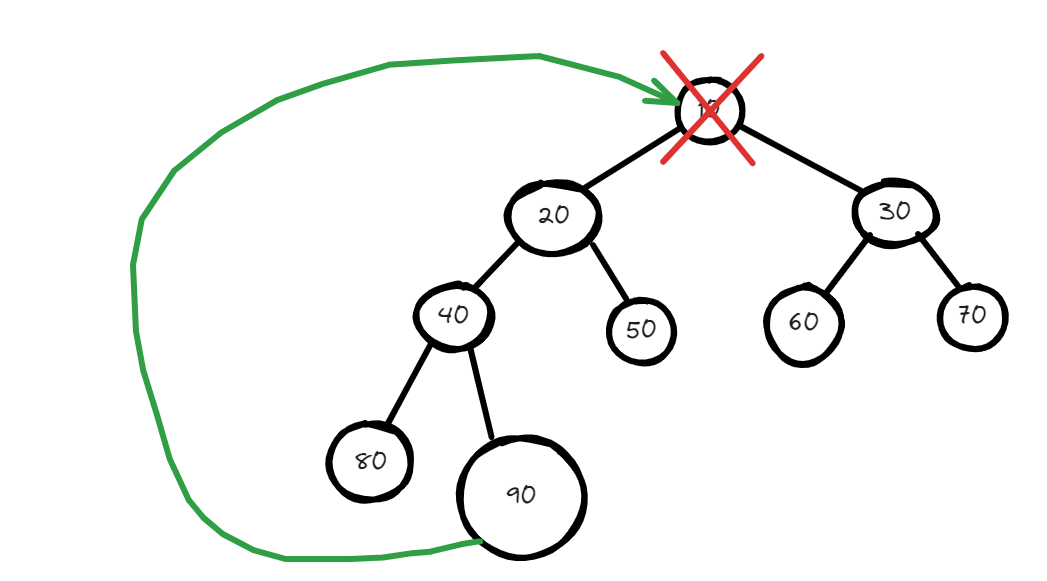
Delete the last element: After the last element has been moved to the root, it is removed from its original position.
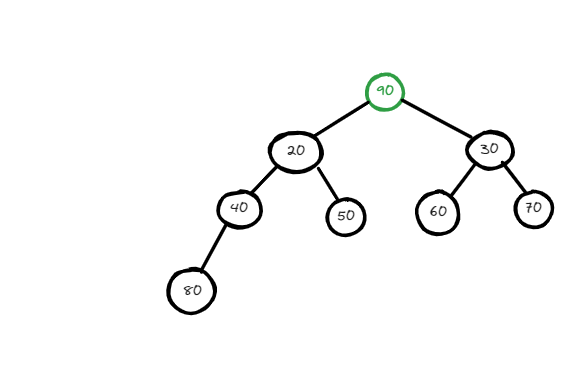
Now if you will check this this is not a valid minheap to make this valid you have to swap this to the lower level node but the question here is to which node so to decide we have to compare both the lower node and whichever will be minimum from these two we will swap that with our node. After comparisons and multiple swap, your heap should finally look like this :

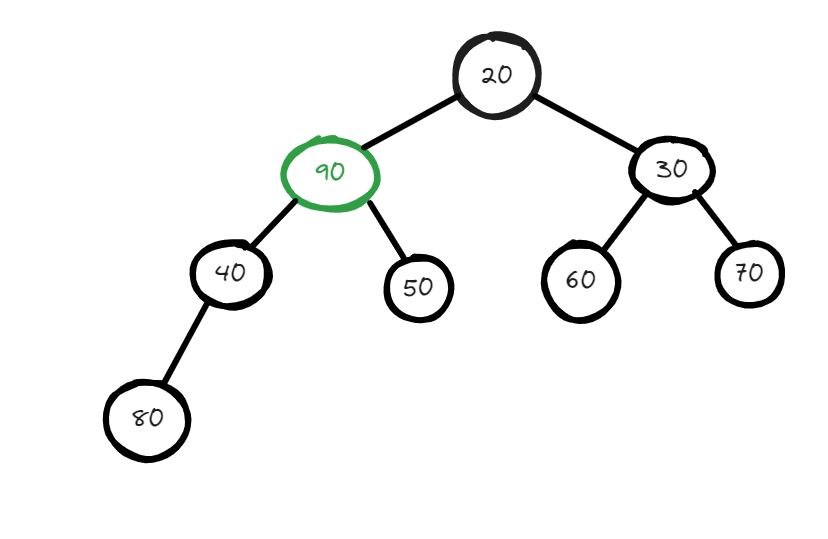
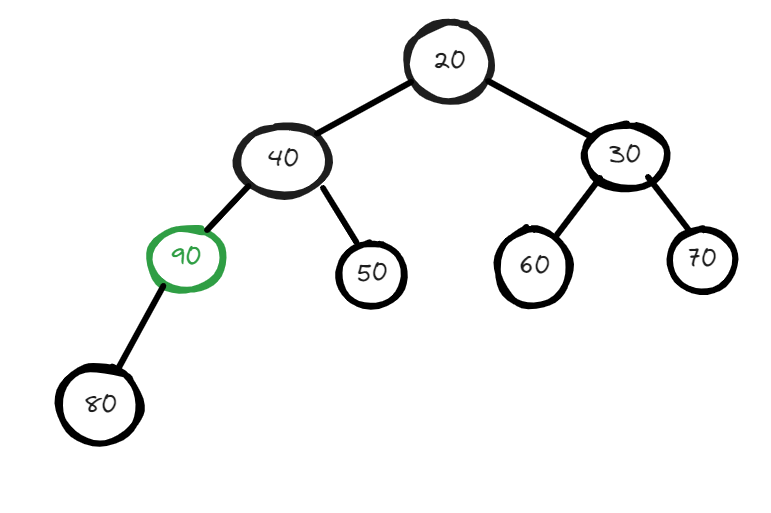
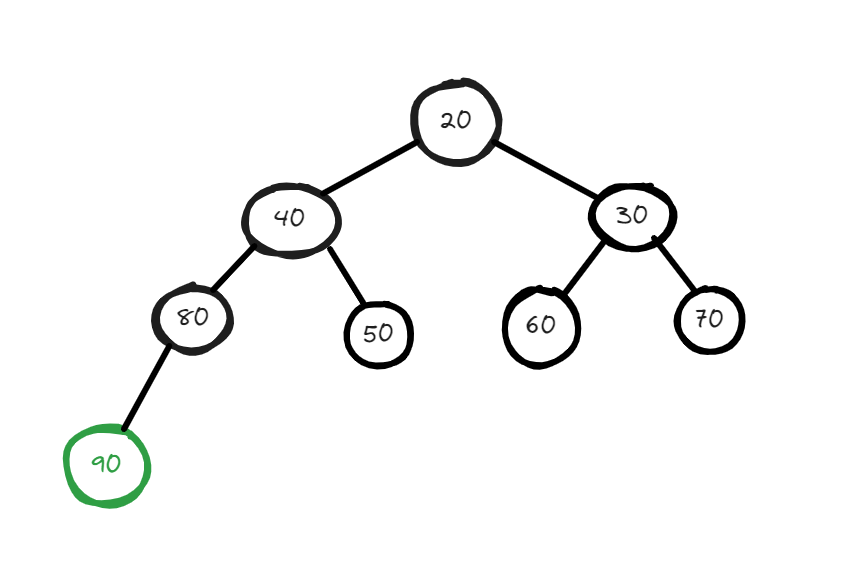
The time complexity for the deletion of a node from the heap is O(log(n)).

Heap Sort:

Heap Sort is a popular and efficient sorting algorithm that uses a binary heap data structure. The process of Heap sorting involves building a Heap data structure with the elements of the array and then utilizing the Heap to sort the array.

Here's a step-by-step explanation of how Heap Sort works:

Build a Heap: The first step is to build a heap from the given input array. This can be a max heap or a min-heap.
Delete the Root: The next step is to delete the root from the heap. If it's a max heap, the root will be the maximum element, and if it's a min heap, the root will be the minimum element.
Heapify the Root: After the root has been replaced, the heap property might be disturbed. Therefore, you need to heapify the root again.
Repeat: Repeat steps 2 and 3 until the heap contains only one element.

The sorted array is obtained by reversing the order of the elements in the input array.

Heap Sort is an in-place sorting algorithm, which means it does not require any extra space for sorting. It also has a running time of O(n log n), making it very efficient for large datasets.

Building of a minheap:

Building a Min Heap involves the following steps :

Initialize the heap: Start by initializing an empty heap. This can be done using an array or a list.
Insert elements into the heap: Insert the elements from your dataset into the heap one by one.
Heapify each inserted element: After inserting an element, you need to restore the heap property. This is done by comparing the inserted element with its parent and moving the inserted element up the heap (i.e., swapping it with its parent) until it’s in a position where it’s less than or equal to its parent. This process is often called “percolating up” or "heapify-up".
Repeat the process: Repeat this process for all elements in your dataset.

// Initialize an empty heap
let heap = [];

// Function to insert a value into the heap
function insert(value) {
    // Add the value to the end of the heap
    heap.push(value);
    // Restore the heap property by moving the value up the heap if necessary
    heapifyUp(heap);
}

// Function to restore the heap property after inserting a value
function heapifyUp(heap) {
    // Start with the last element in the heap
    let index = heap.length - 1;
    const element = heap[index];

    // While the element has a parent
    while (index > 0) {
        // Calculate the parent's index
        let parentIndex = Math.floor((index - 1) / 2);
        let parent = heap[parentIndex];

        // If the parent is less than or equal to the element, the heap property is restored
        if (parent <= element) break;

        // Otherwise, swap the parent and the element
        heap[index] = parent;
        heap[parentIndex] = element;
        // Move up to the parent's level
        index = parentIndex;
    }
}

// Function to delete the root from the heap
function deleteRoot() {
    // If the heap is empty, return null
    if (heap.length === 0) {
        return null;
    }
    // Save the root's value
    let root = heap[0];
    // Replace the root with the last element in the heap
    heap[0] = heap[heap.length - 1];
    // Remove the last element from the heap
    heap.pop();
    // Restore the heap property by moving the new root down the heap if necessary
    heapifyDown(heap);
    // Return the original root's value
    return root;
}

// Function to restore the heap property after deleting the root
function heapifyDown(heap) {
    // Start with the root
    let index = 0;
    const length = heap.length;
    const element = heap[0];

    // While the element has at least one child
    while (true) {
        // Calculate the children's indices
        let leftChildIndex = 2 * index + 1;
        let rightChildIndex = 2 * index + 2;
        let leftChild, rightChild;
        let swap = null;

        // If the left child exists and is less than the element, plan to swap with the left child
        if (leftChildIndex < length) {
            leftChild = heap[leftChildIndex];
            if (leftChild < element) {
                swap = leftChildIndex;
            }
        }

        // If the right child exists and is less than the element (or the left child, if a swap was already planned), plan to swap with the right child
        if (rightChildIndex < length) {
            rightChild = heap[rightChildIndex];
            if (
                (swap === null && rightChild < element) ||
                (swap !== null && rightChild < leftChild)
            ) {
                swap = rightChildIndex;
            }
        }

        // If no swap was planned, the heap property is restored
        if (swap === null) {
            break;
        }

        // Otherwise, swap the element with the smaller child
        heap[index] = heap[swap];
        heap[swap] = element;
        // Move down to the child's level
        index = swap;
    }
}

The time complexity for Heap Sort is O(n log n) in all cases (best case, average case, and worst case). This is because the heap sort algorithm consists of building a heap (which takes O(n) time) and then performing n delete operations (each of which takes O(log n) time). Therefore, the total time complexity is O(n + n log n) = O(n log n).

Conclusion

In this blog, we’ve explored the world of heap data structures, starting from the basics of trees and binary trees, and moving on to heaps. We’ve learned how heaps, particularly min heaps, are constructed and how operations like insertion and deletion are performed.

We also delved into Heap Sort, an efficient sorting algorithm with a time complexity of O(n log n), making it a powerful tool for handling large datasets.

Understanding heaps and their applications in algorithms like Heap Sort is a crucial part of mastering data structures. As we continue our journey in computer science, let’s keep exploring, learning, and coding!

Happy coding! 😊

Understanding Heaps: A Deep Dive into Data Structures

Table of contents