Is Graph Bipartite?
 Anurag Kumar
Anurag Kumar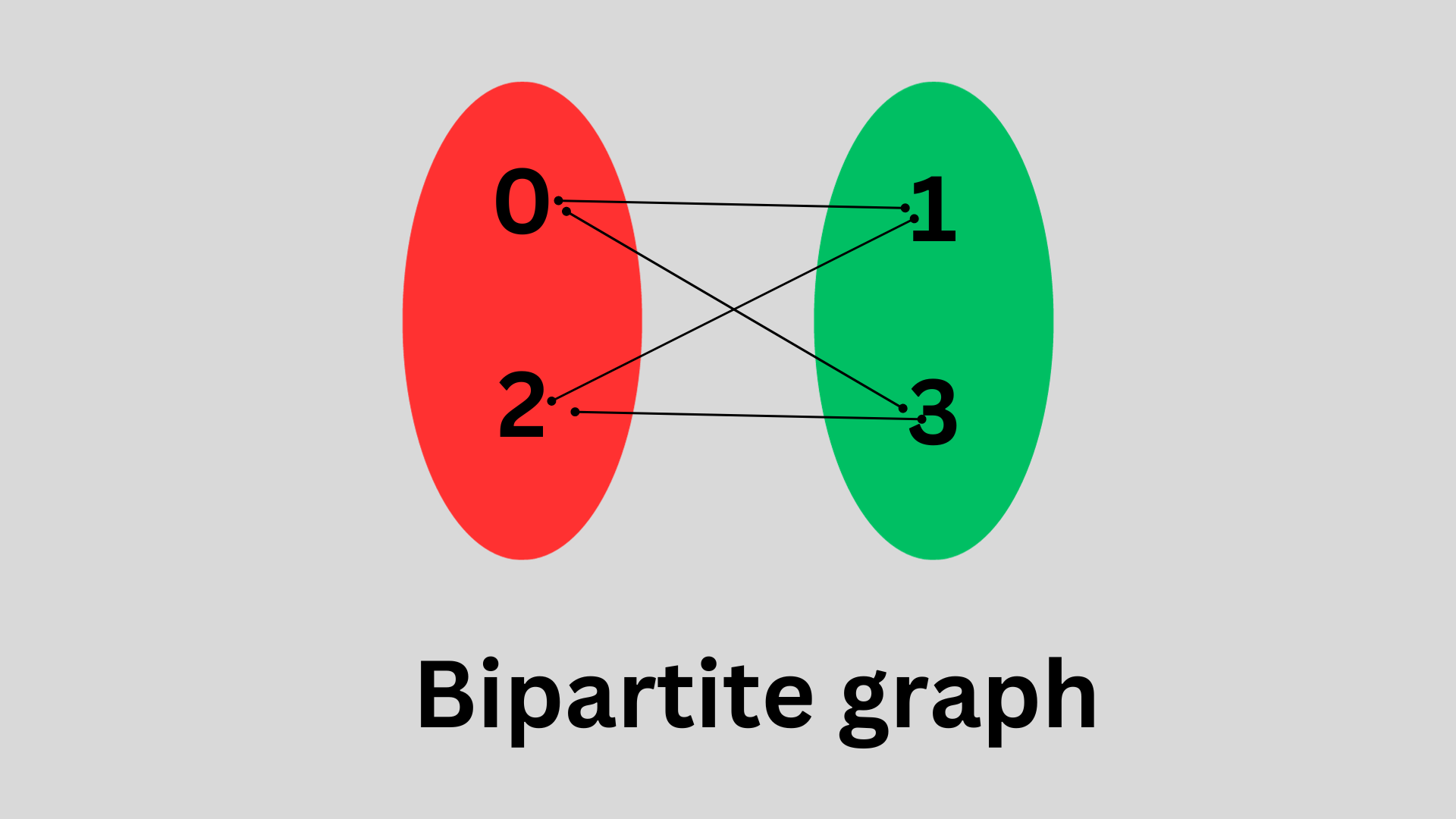
This is the Medium level question of Leetcode Link.
This question is asked in Companies like:-
Samsung | Facebook | PegaSystems |GoldmanSachs | Uber | eBay | Walmart | OYO | Triology | Bunzo
Problem
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
There are no self-edges (
graph[u]does not containu).There are no parallel edges (
graph[u]does not contain duplicate values).If
vis ingraph[u], thenuis ingraph[v](the graph is undirected).The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
Return trueif and only if it is**bipartite.
Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Solution:
There are various methods to solve this problem, and I will explain through graph coloring technique and I'm going to use DFS approach to solve this problem.
As per the bipartite graph definition:
A graph is bipartite if the nodes can be partitioned into two independent sets
AandBsuch that every edge in the graph connects a node in setAand a node in setB.
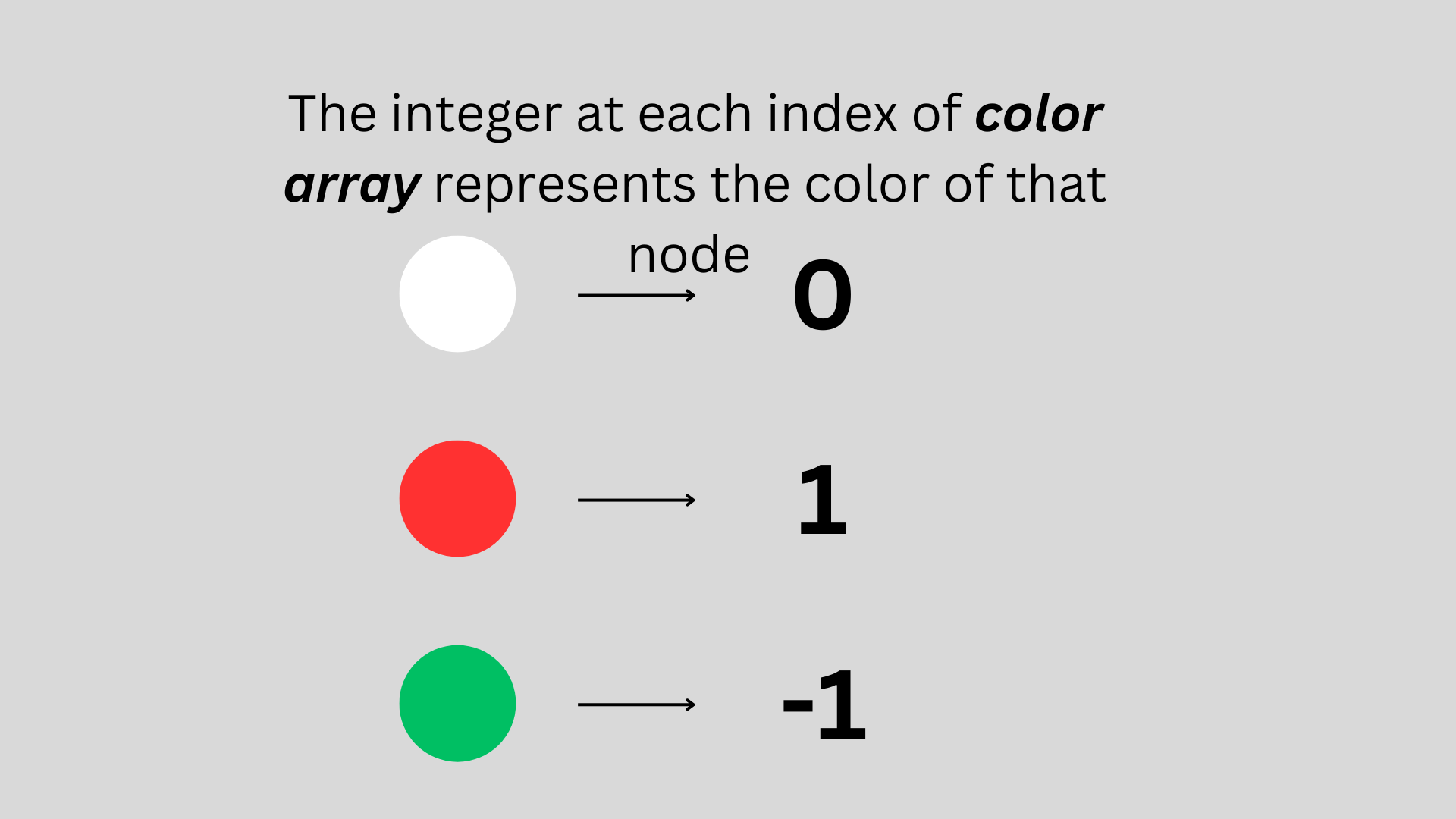
Initially, we take a color array of size number of nodes.
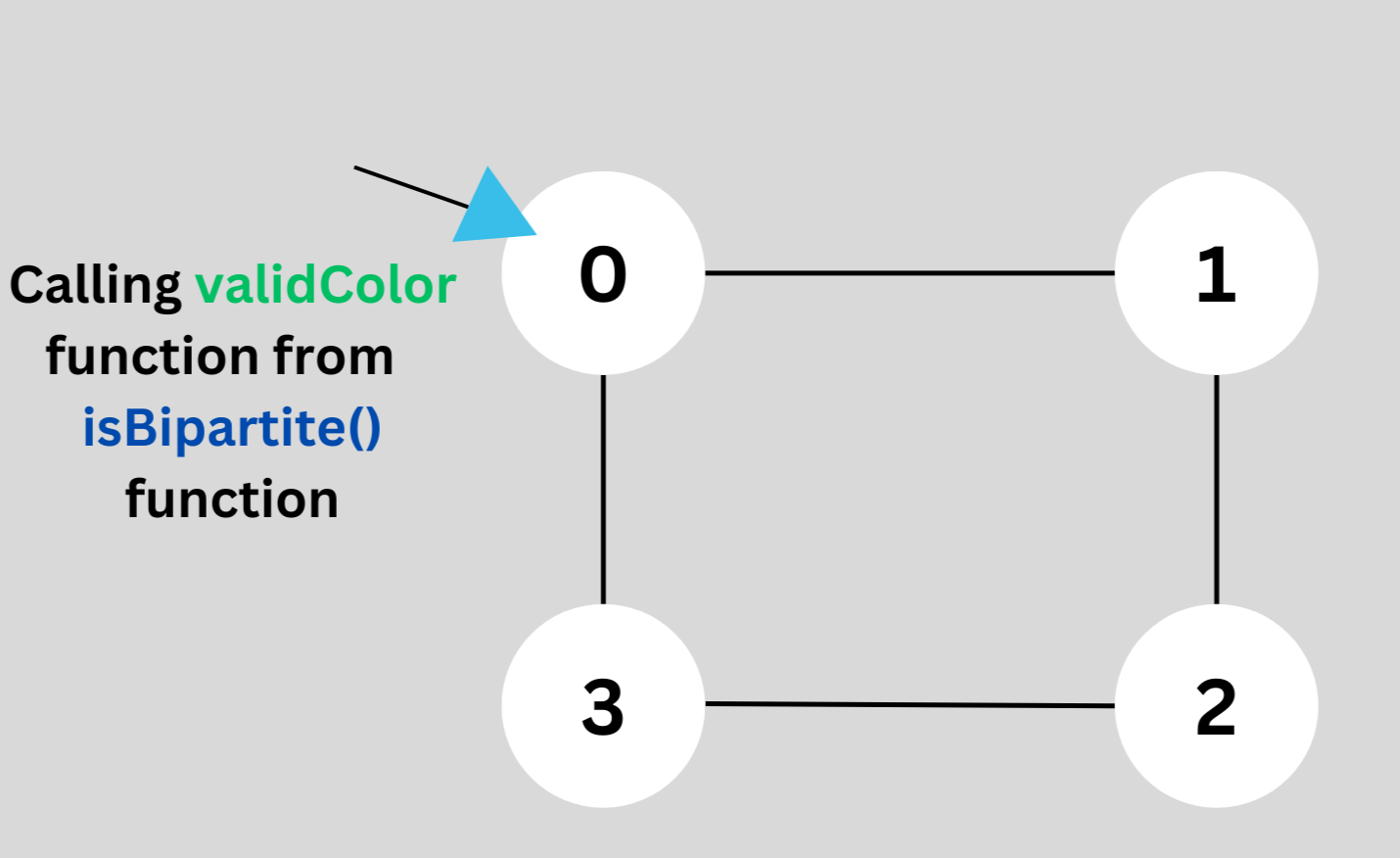
In the isBipartite() function the validColor() function is called for each node which is not colored.
for(int i=0;i<n;i++){
if(color[i]==0 && !validColor(graph, color, 1 , i)){
return false;
}
}
Then color that node with c=1 which is sent initially.
Inside the validColor() function, the recursion call of the validColor() is happening and by that way we are reaching the connected node of the previous node.
So we reached the node 1 and color that node too but with a different color as the adjacent node must not be colored with the same node.
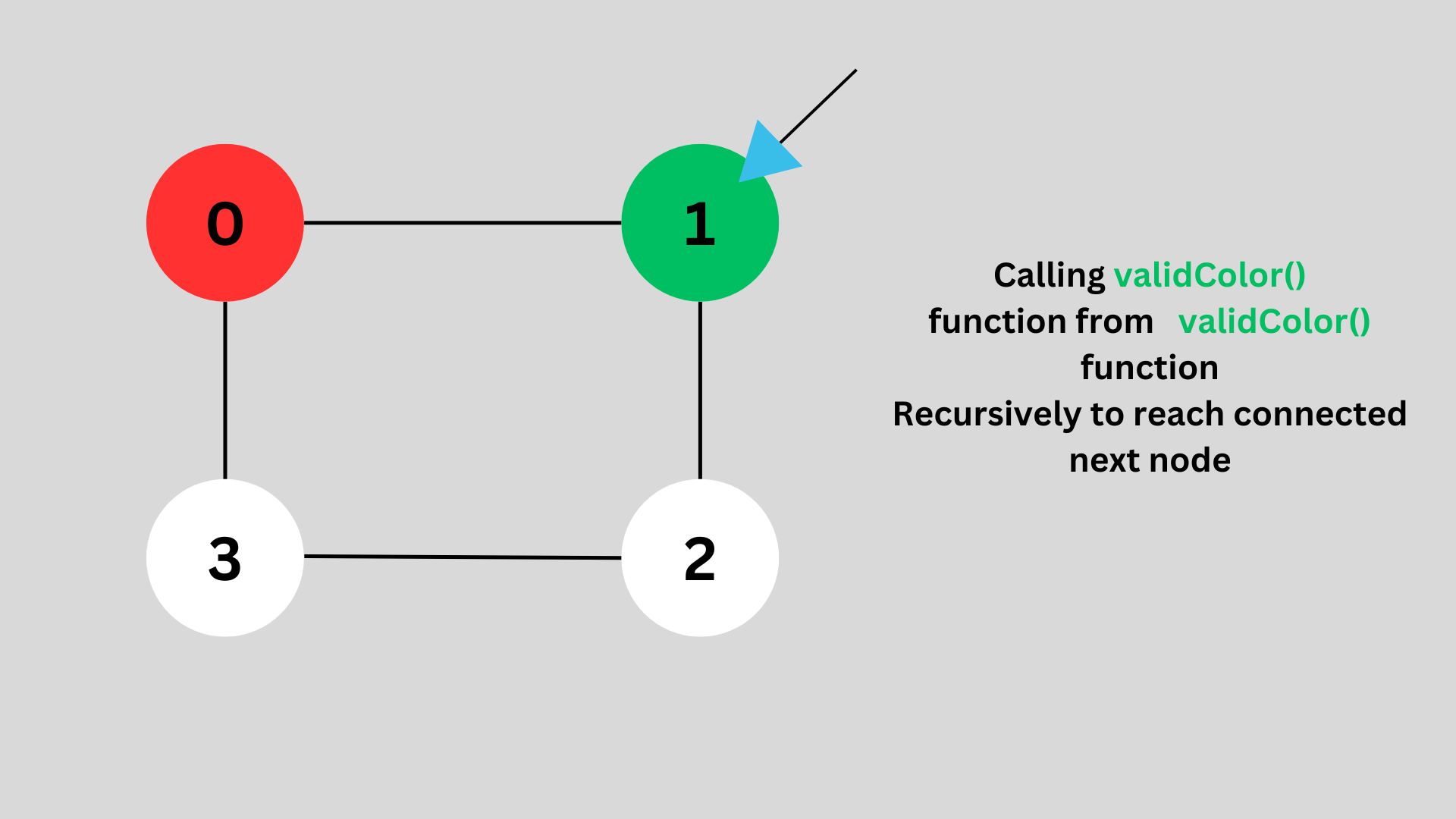
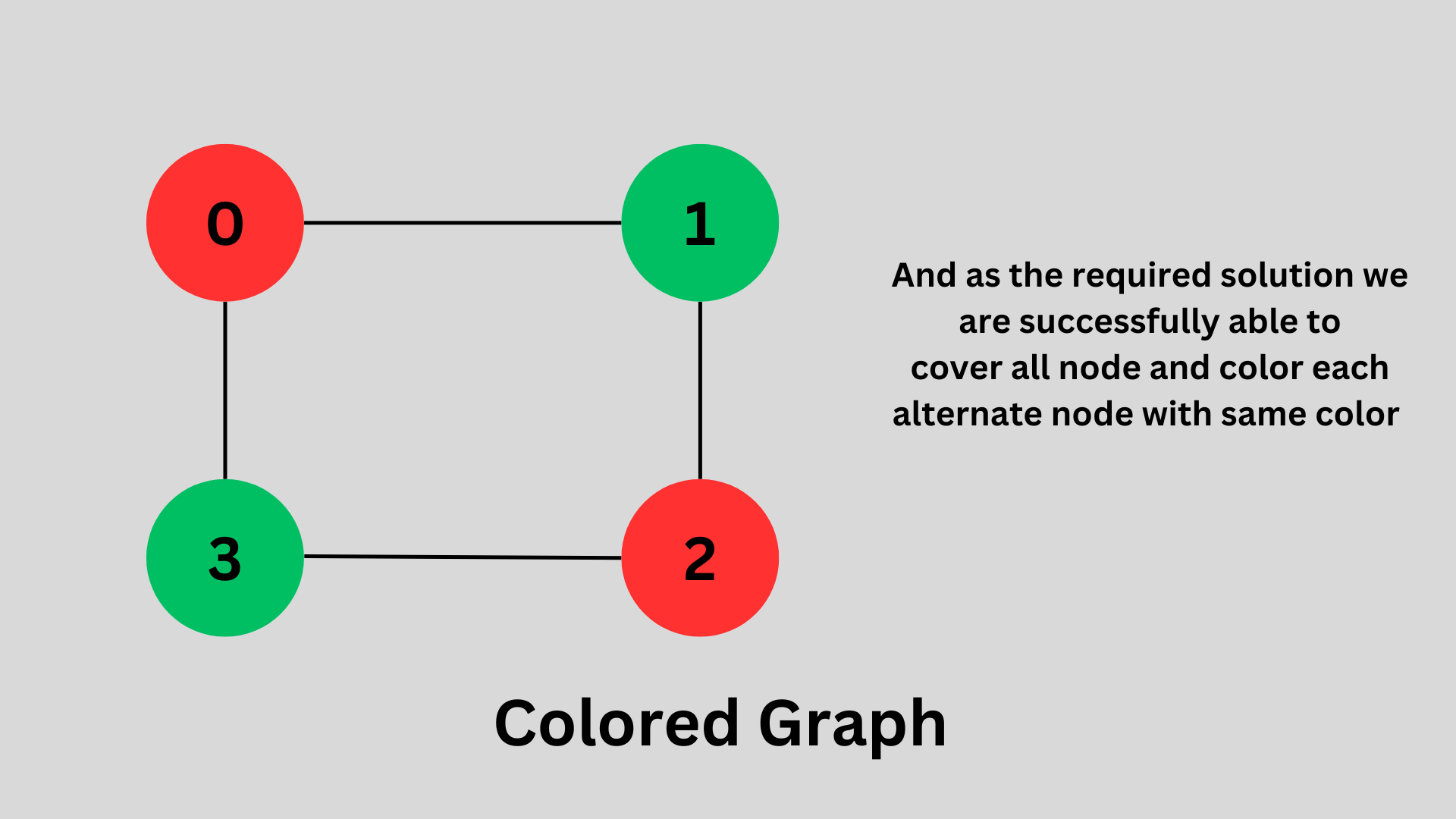
So we'll go one to all nodes recursively and color each node with two color, with no any adjacent node with the same color.
Afterwards, when the recursive function validColor() returned to isBipartite function in the for loop all the node is colored successfully and then return true; is called.
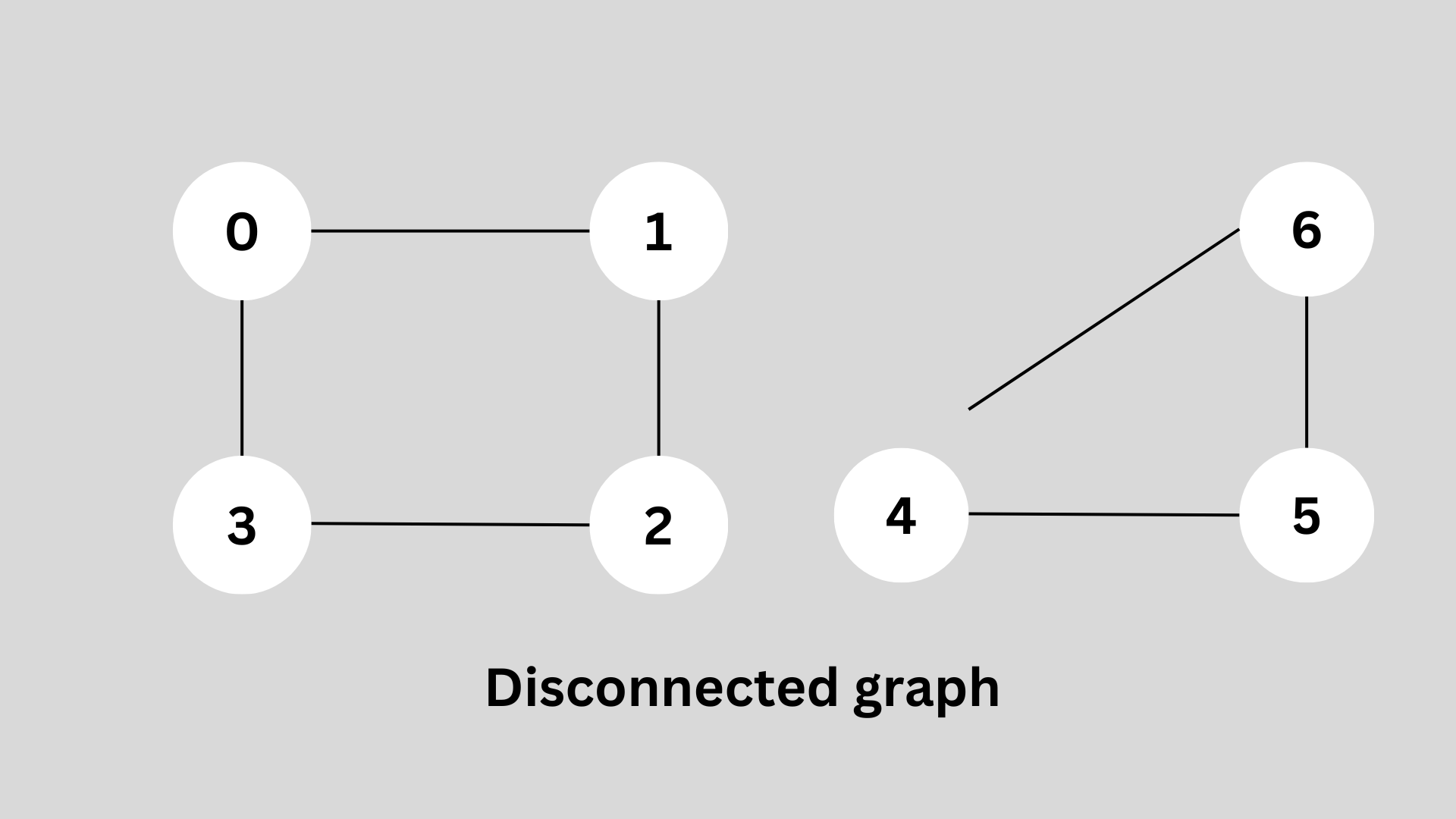
You might be thinking that's why I'm calling validColor() function for all nodes, in the isBipartite as we saw in the given example explanation by calling for one node it's giving us the solution.
So, this is a graph problem and any one node or group of nodes can exist separately. As shown in the below figure:-
Code
class Solution {
public boolean isBipartite(int[][] graph) {
int n = graph.length;
int[] color = new int[n];
for(int i=0;i<n;i++){
if(color[i]==0 && !validColor(graph, color, 1 , i)) return false;
}
return true;
}
public boolean validColor(int[][] graph, int[] color, int c , int node){
if(color[node]!= 0){
return color[node]==c;
}
color[node] = c;
for(int i : graph[node]){
if(!validColor(graph, color, -c , i)) return false;
}
return true;
}
}
Thank you, folks, for reading till the end, if you find this solution blog helpful please like this blog.
If you have any suggestion then please drop in the comment section.
Check out my Portfolio.
Subscribe to my newsletter
Read articles from Anurag Kumar directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Anurag Kumar
Anurag Kumar
Hi, I’m Anurag Kumar, a Software Engineer who loves exploring the latest technologies and sharing insights to help others grow. With a focus on web development and DevOps, I enjoy writing about practical tips, emerging trends, and tools that make developers' lives easier. My goal is to keep my blogs simple, engaging, and useful for everyone—whether you're just starting out or looking to level up your skills. Follow me for friendly and accessible content that bridges the gap between learning and doing! Connect me on twitter : https://x.com/AnuragS41695054