Arrays ,Sliding Window ,Prefix sum and n Pointers Problems
 Paras kaushik
Paras kaushikTable of contents
- Set Matrix zeros
- Pascals Triangle
- Next Permutation 🌟
- Kadane's Algorithm
- Sort and Array of 0's and 1's/Even-Odds without sort fn
- Sort an Array for 0's, 1's and 2's without sort()
- Stock Buy and Sell single transaction
- Rotate Matrix
- Merge overlapping subintervals
- Merge two sorted arrays without extra space 🌟
- Find the duplicate in an array of N+1 integers 🌟
- Repeat and Missing Number
- Count Inversions in Array
- Search a sorted 2D Matrix
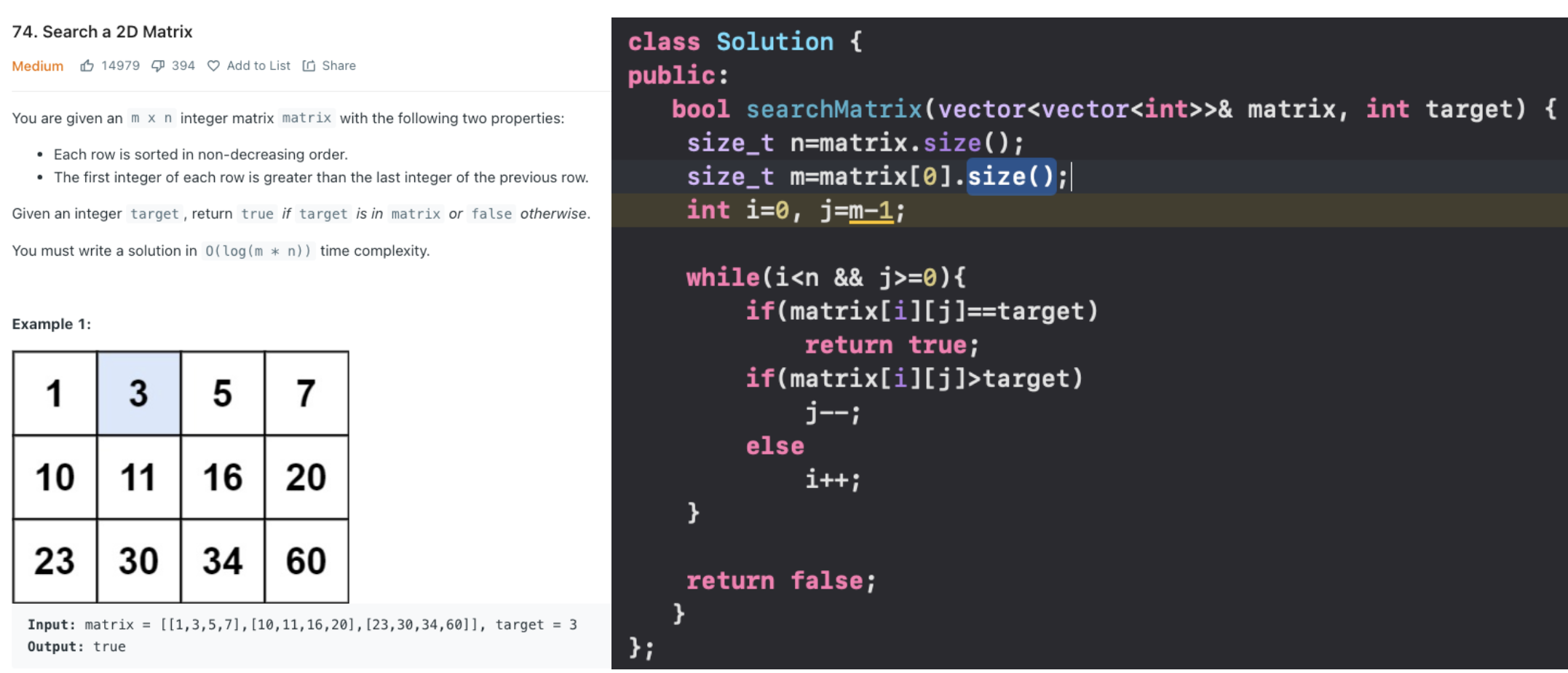
- Pow(x,n)
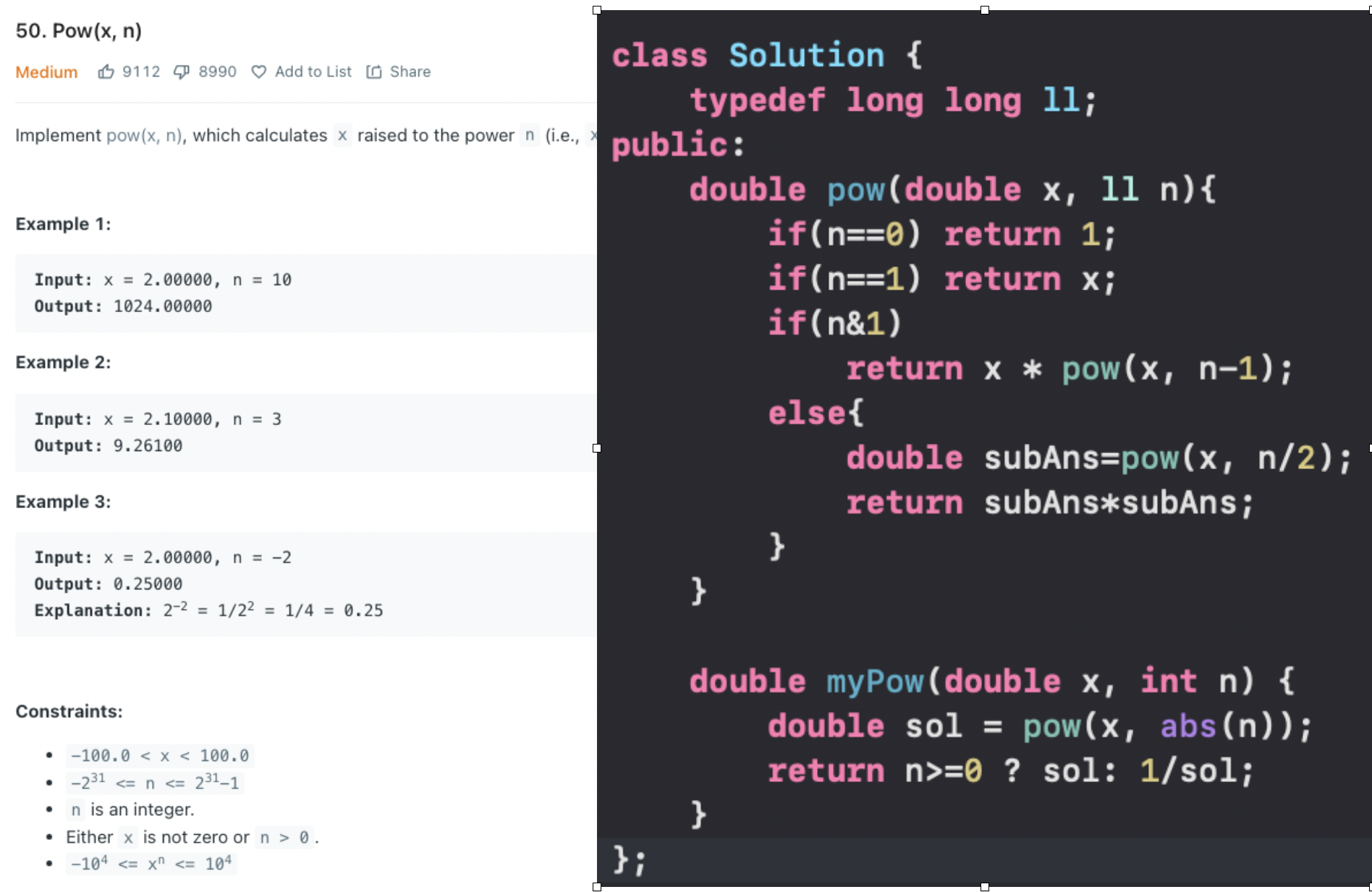
- Majority Element (>N/2 times)
- Majority Element (n/3 times) 🌟
- Unique Paths - nCr
- Reverse Pairs
- 2Sum
- 3 Sum 🌟
- 4 Sum 🌟
- Longest Consecutive Sequence
- Longest subarray with zero sum (classic Prefix sum problem) 🌟
- Number of Subarrays with XOR K 🌟
- Longest Substring Without Repeating Characters (Classic Sliding window)
- Stock Buy and Sell any number of transactions
- Stock buy and sell with Cooldown / with fee
- Stock buy and sell at most 2 transactions allowed (divide and conquer strategy)
- Stock buy and sell at most k transactions allowed (DP)
- Find First Missing Positive Number 🌟🌟
- Implement Merge Sort
- Remove Duplicates from Sorted Array

Set Matrix zeros
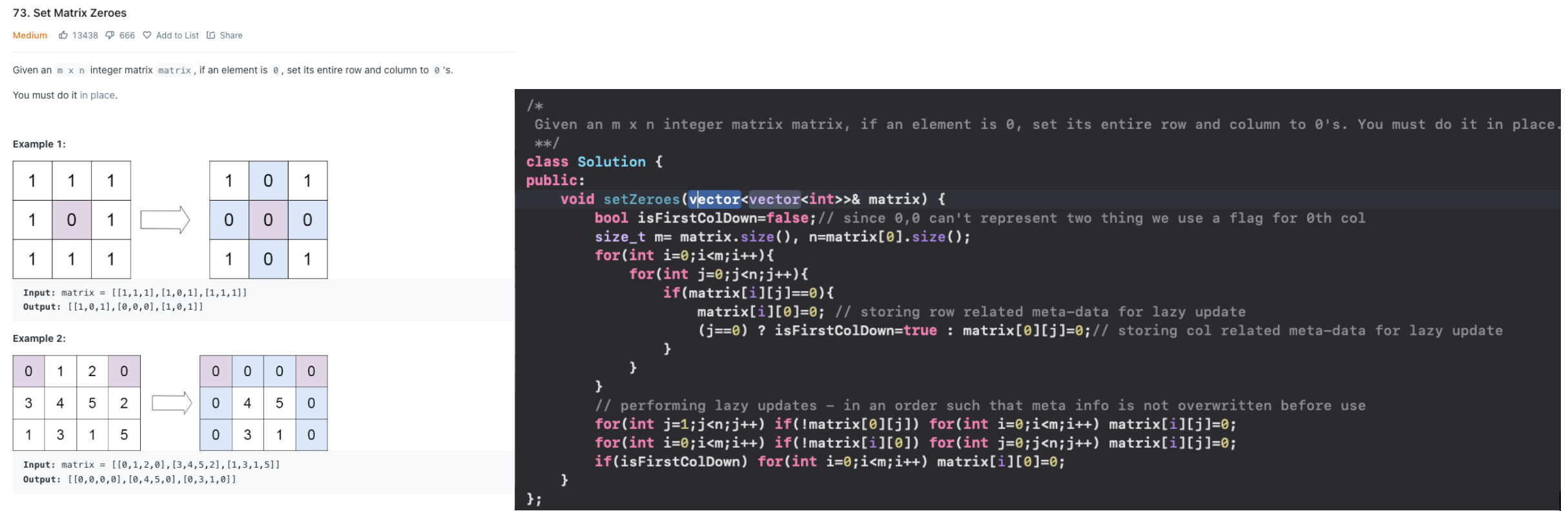
IDEA:
To solve this problem, use the first row and column of the matrix to store markers indicating if a row or column should be set to 0's. this way we don't have to use any extra space
Iterate through the matrix, and if an element is 0, mark the corresponding row and column.
Finally, update the matrix using these markers, making sure not to overwrite metadata before using it.
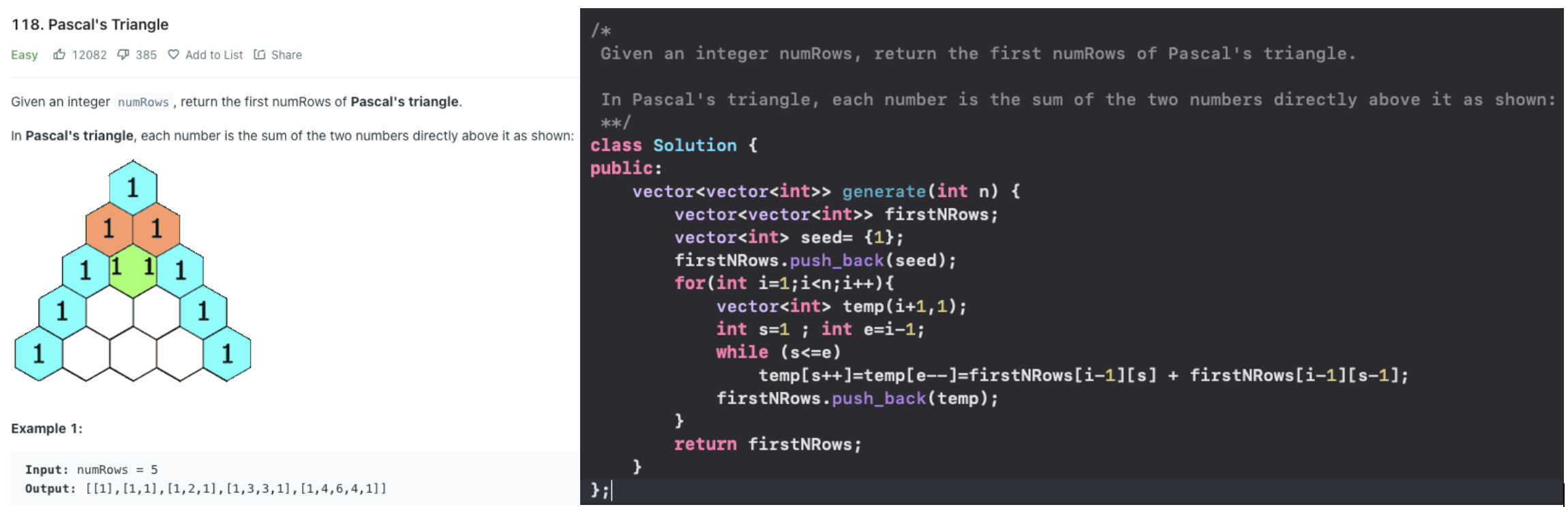
Pascals Triangle
Next Permutation 🌟
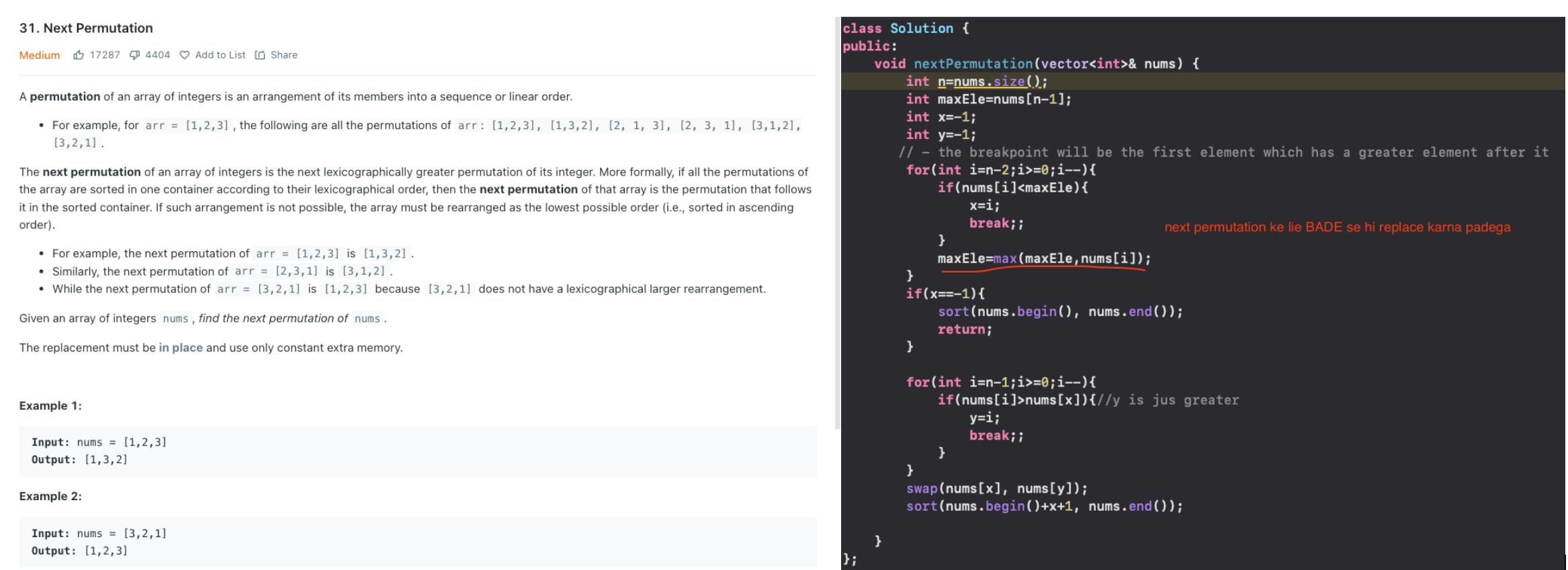
Intuition:
The 'just' next permutation will have a maximised longest matching prefix(as we move further next this matching prefix would decrease in length) and among the rest of the array
We can thus imagine this array divided into two parts, a matching prefix and a suffix the STARTING of which has to be replaced with a greater element
We know a GREATER element has to replace an existing element at the point/index from which next permutation differs the prior permutation
If there is no such element present for a particular prefix - that is not a valid prefix for any subsequent permutation
So after this index we need to pick the element 'just' greater and put that element at this point
The breakpoint will be the first element which has a greater element after ie the first i in the suffix where a[i] < maxElement on the right - lets call it X
Beyond this breakpoint we know array is strictly decreasing
So to find an element 'just' greater than X we can simply traverse from behind - we name this 'just' greater element Y
We swap X and Y
Now since this is beginning of a new prefix the rest of the array after index X can be placed in sorted order
Kadane's Algorithm
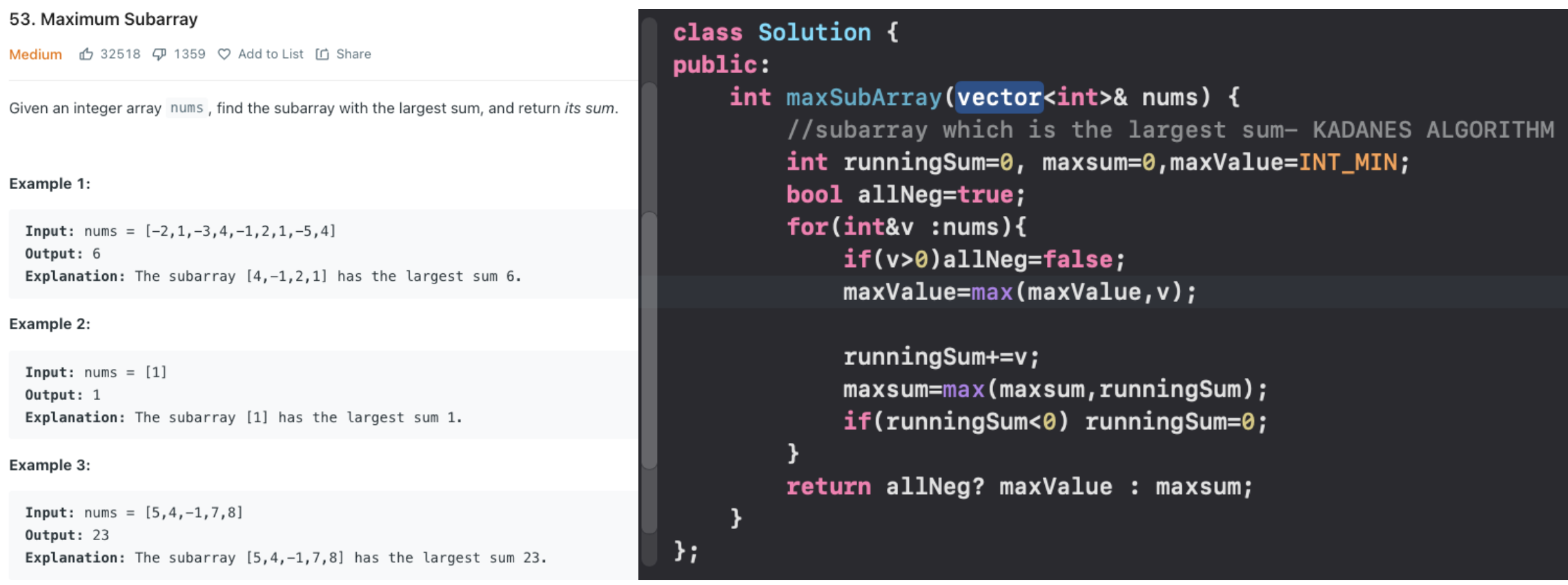
Kadane's Algorithm is a dynamic programming approach used for efficiently finding the maximum sum contiguous subarray within a one-dimensional array of numbers
Sort and Array of 0's and 1's/Even-Odds without sort fn
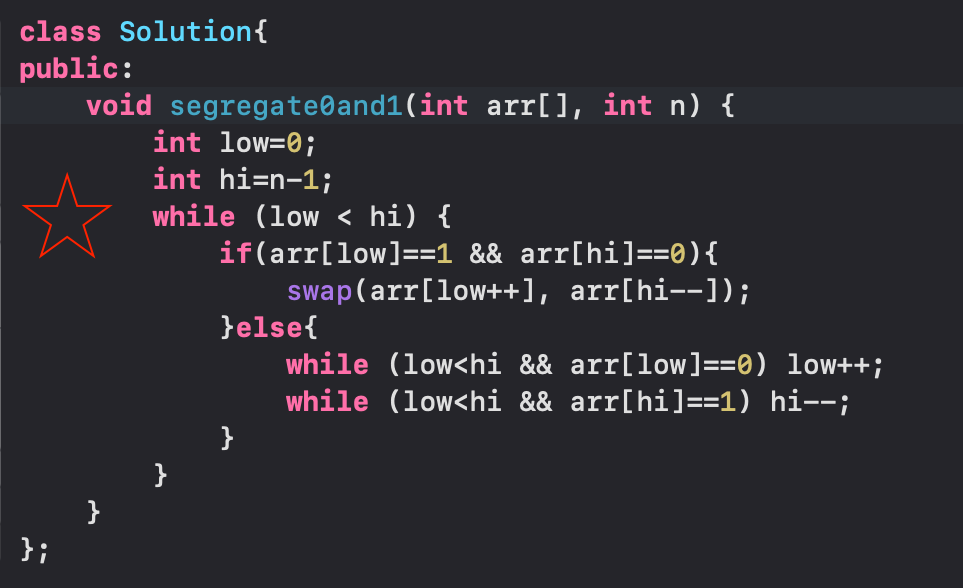
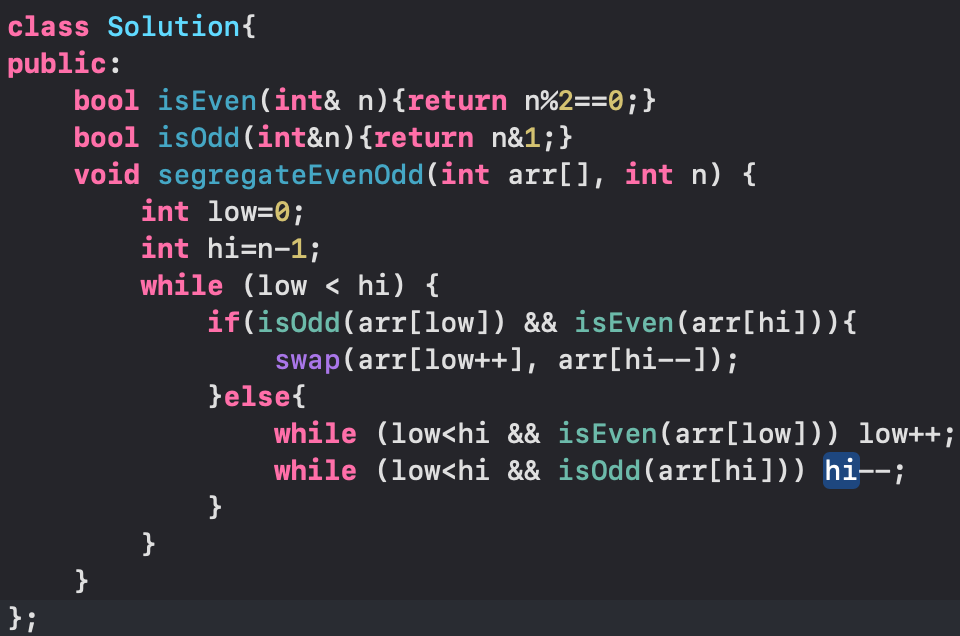
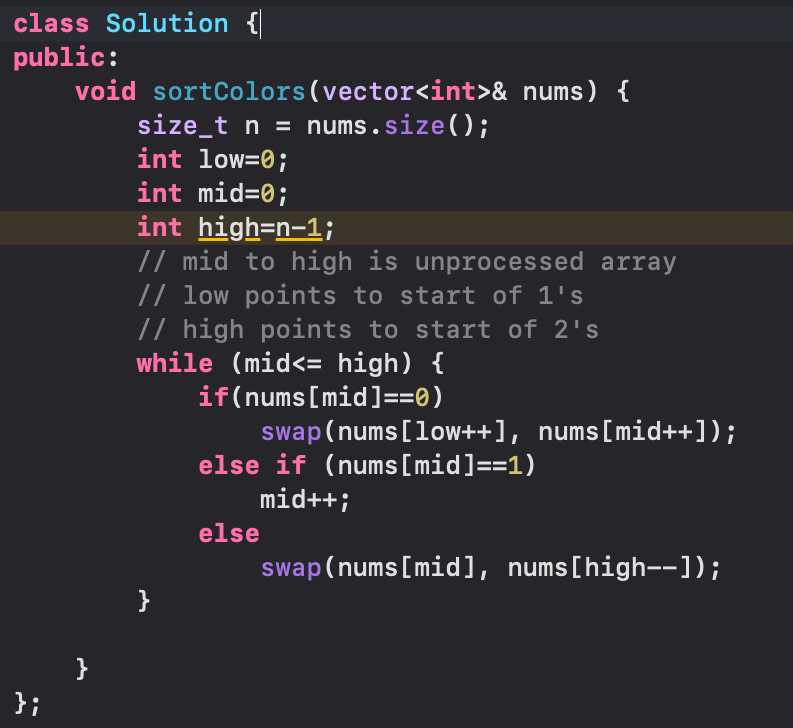
Sort an Array for 0's, 1's and 2's without sort()
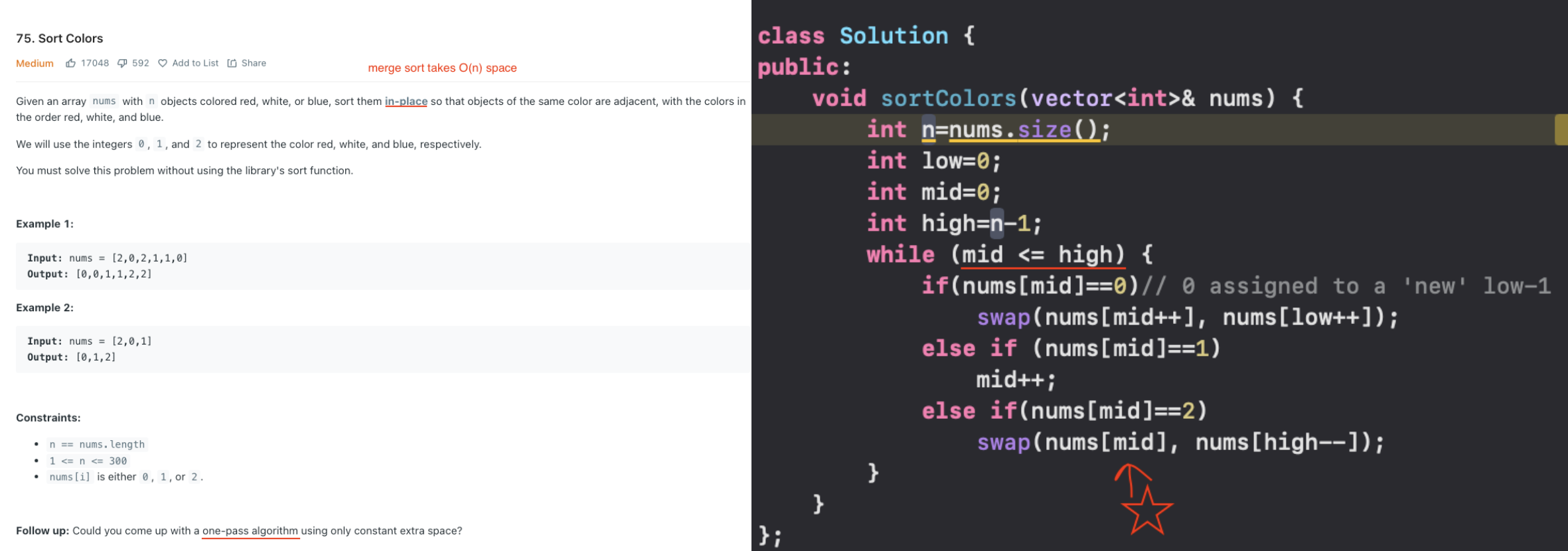
DUTCH NATIONAL FLAG ALGO: WE TAKE THREE POINTERS (LOW,MID,HIGH)
Assume a hypothetical array where
[mid to high] are unseen numbers
0 to low-1 are 0's -> "low" pointer appends to the 0's array
low to mid-1 are 1's-> "mid" pointer appends to the 1's array
high+1 to n-1 are 2's-> "high" pointer prepends to the 2's array
We have to reduce the length of unseen portion to zero (emulation of the algorithm)
OR
low is 1's feeder
high is 2's feeder
Stock Buy and Sell single transaction
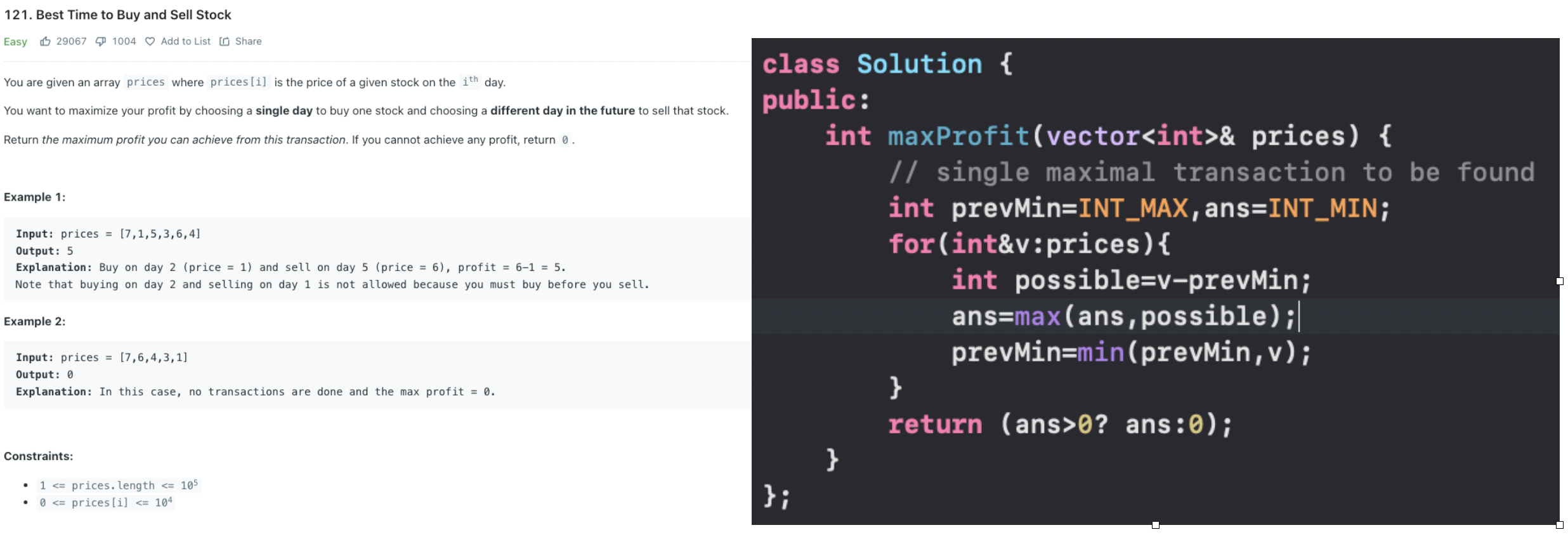
The idea is to simply buy the lowest and then sell when price is highest
Rotate Matrix
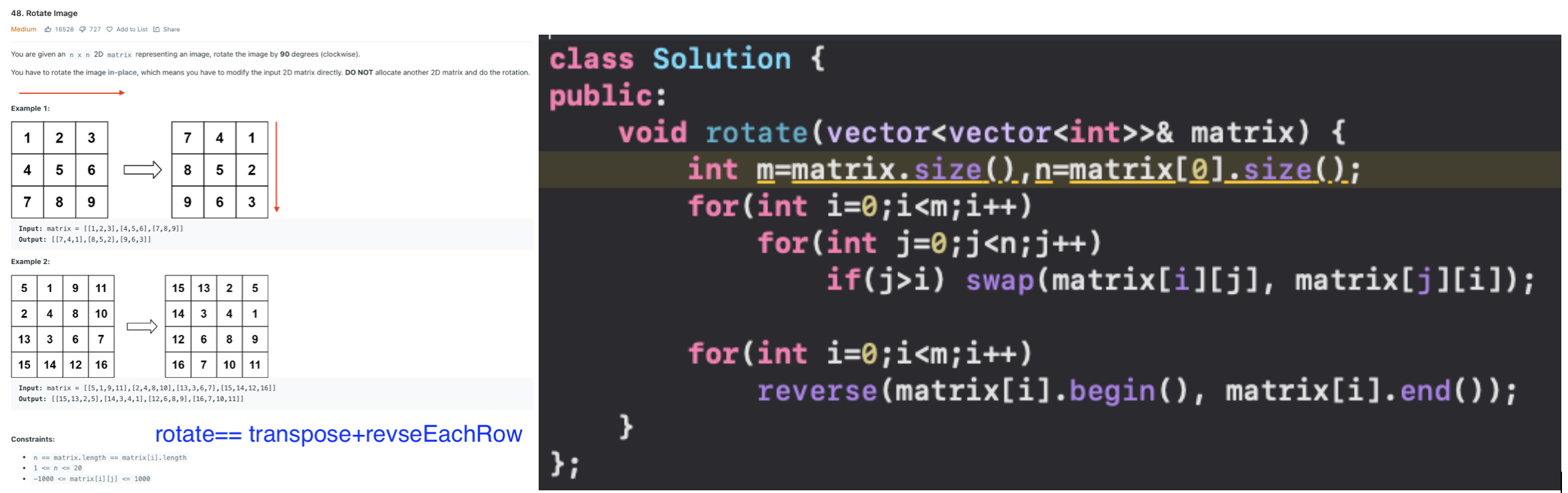
We will take transpose of the matrix and then reverse each row
Merge overlapping subintervals
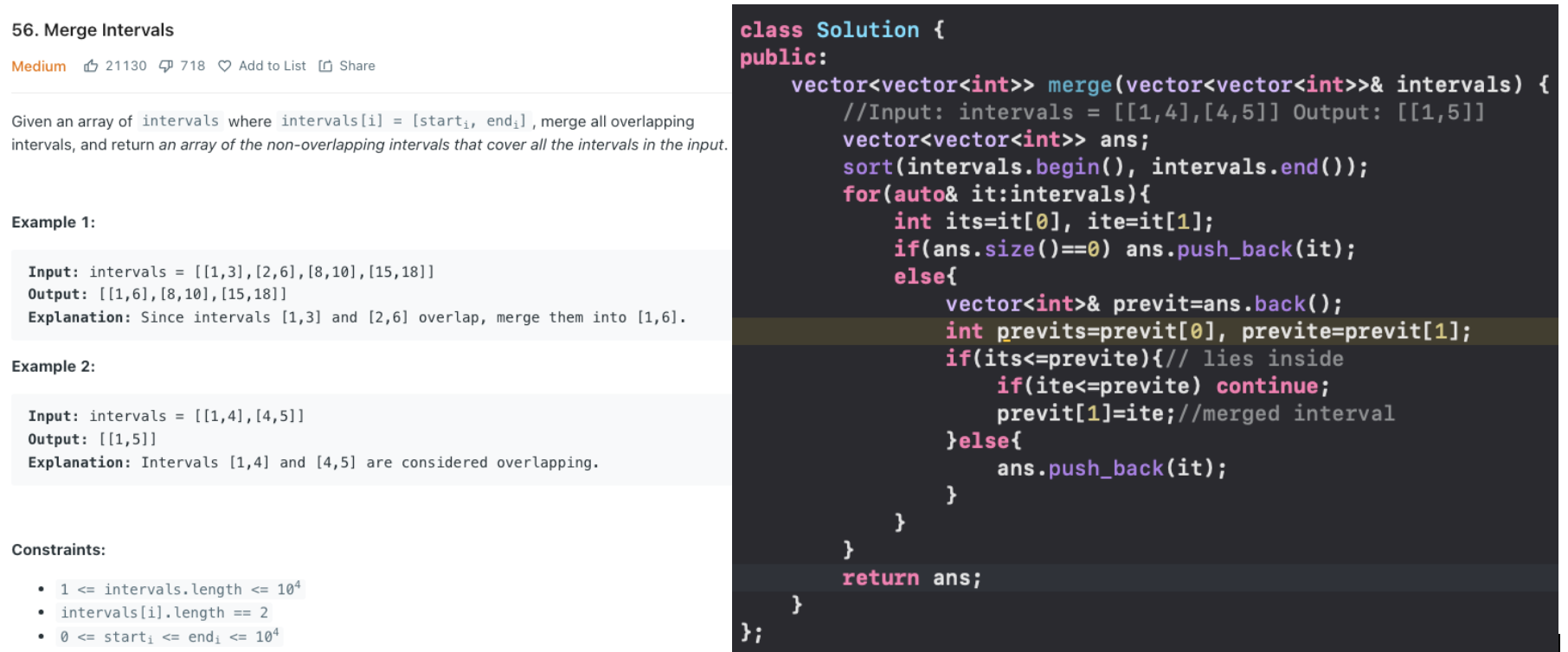
We sorted by start time, as then the adjacent intervals are most likely to overlap
Merge two sorted arrays without extra space 🌟
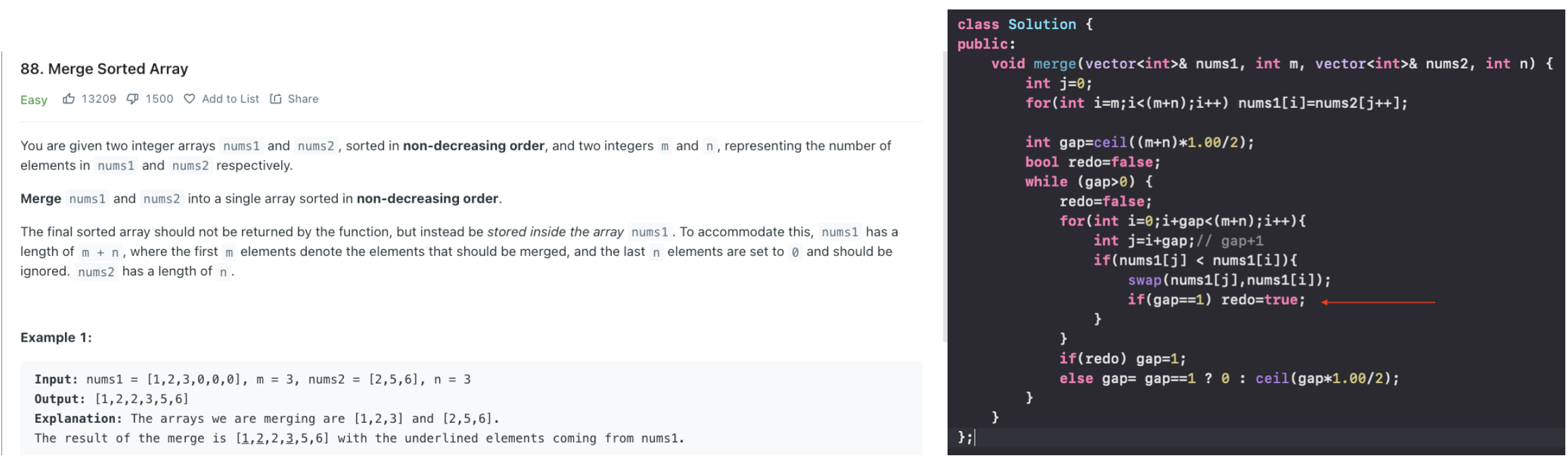
Time complexity here is nlogn (similar to merge sort)
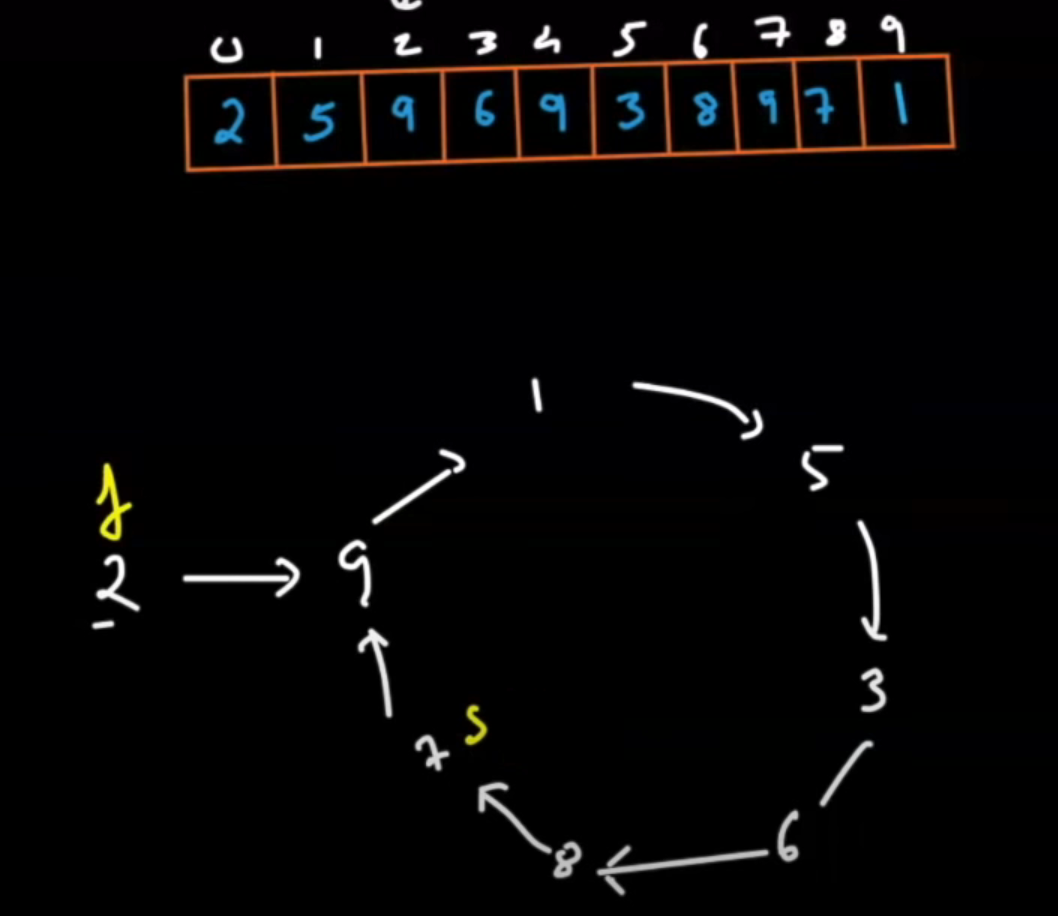
Find the duplicate in an array of N+1 integers 🌟
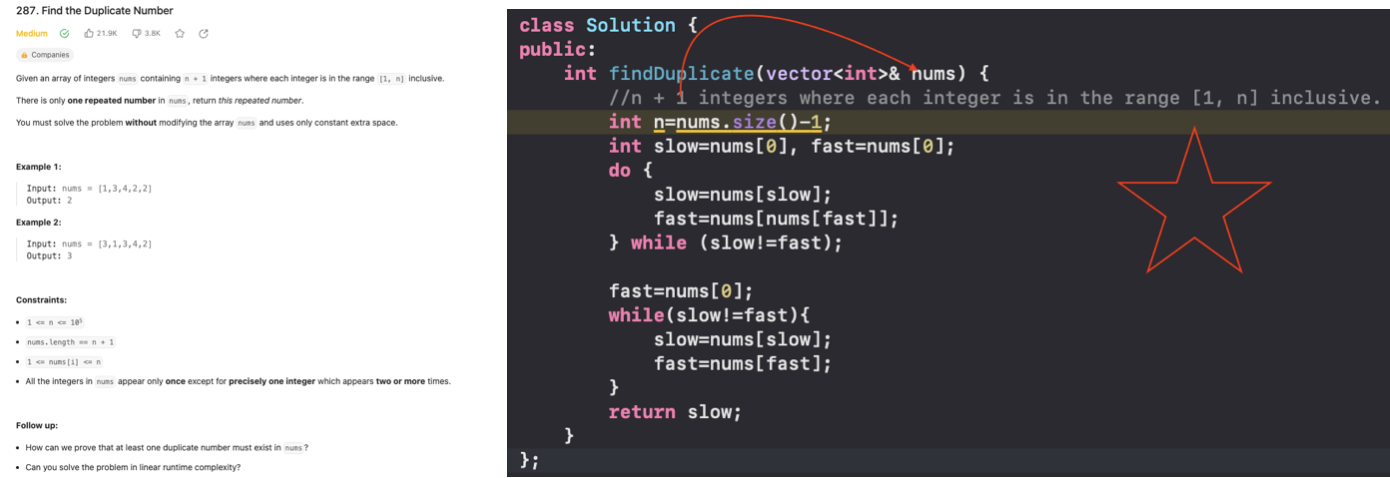
We pay attention to the fact that the array values are bound ie [1,n], this can be reduced to Floyd cycle detection algorithm
Repeat and Missing Number
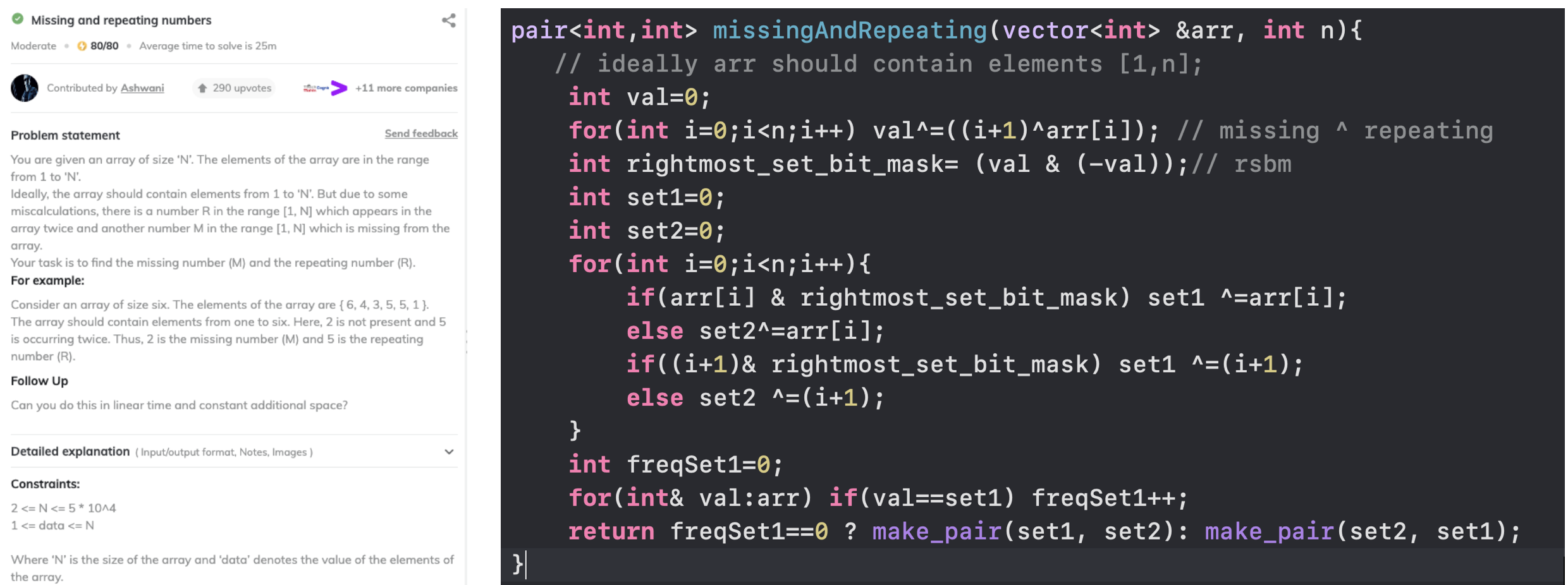
Since we took XOR we are sure both missing and repeating will lie is separate sets
The set in which the missing number exits , gets all other elements which have a pair in the original array they cancel on taking xor leaving the missing one behind
The set in which the repeating number exits , gets all other elements which have a pair in the original array, the repeating one is the only element here occurring thrice they cancel on taking xor leaving the repeating one behind
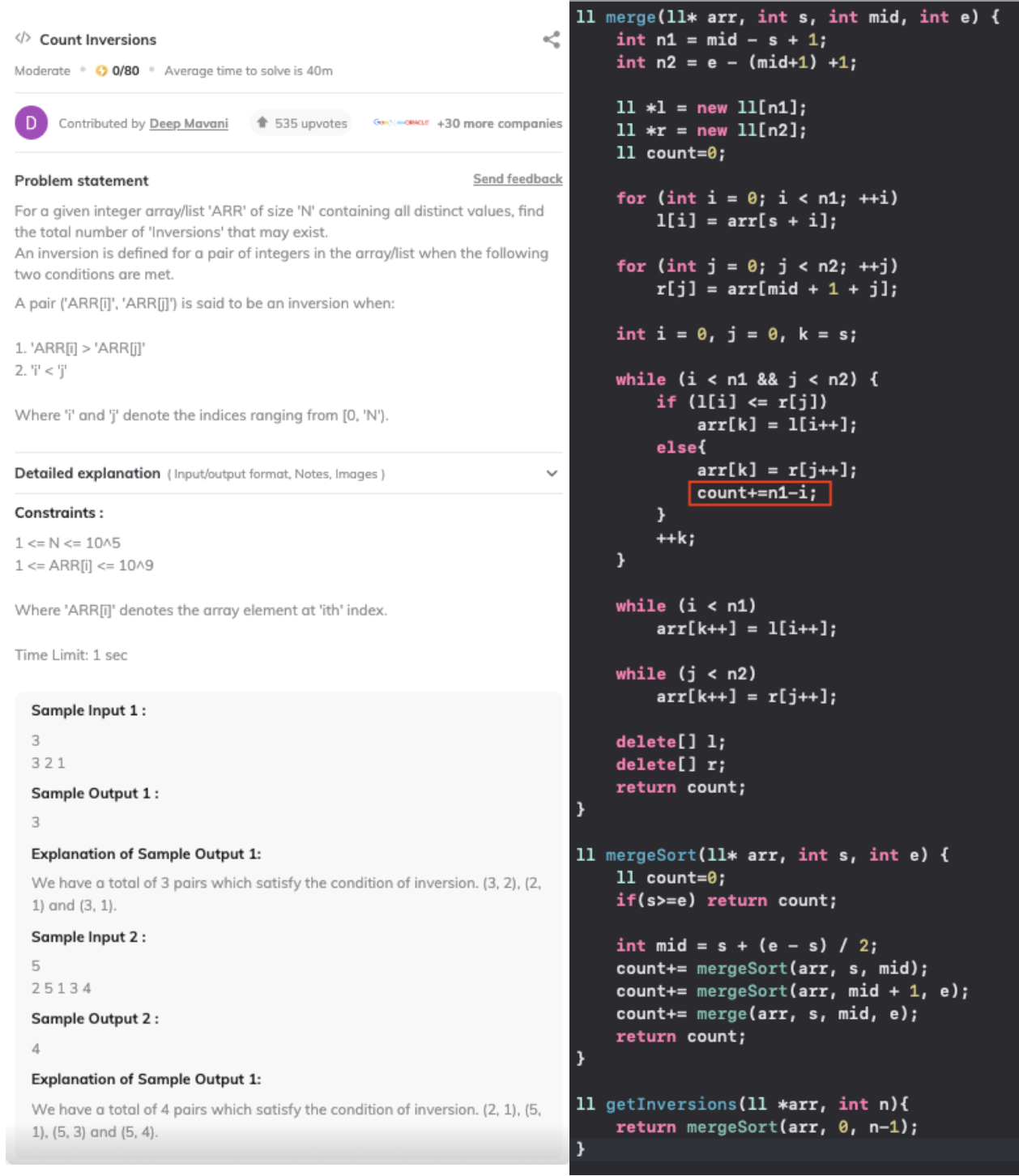
Count Inversions in Array
Search a sorted 2D Matrix
Pow(x,n)
Majority Element (>N/2 times)
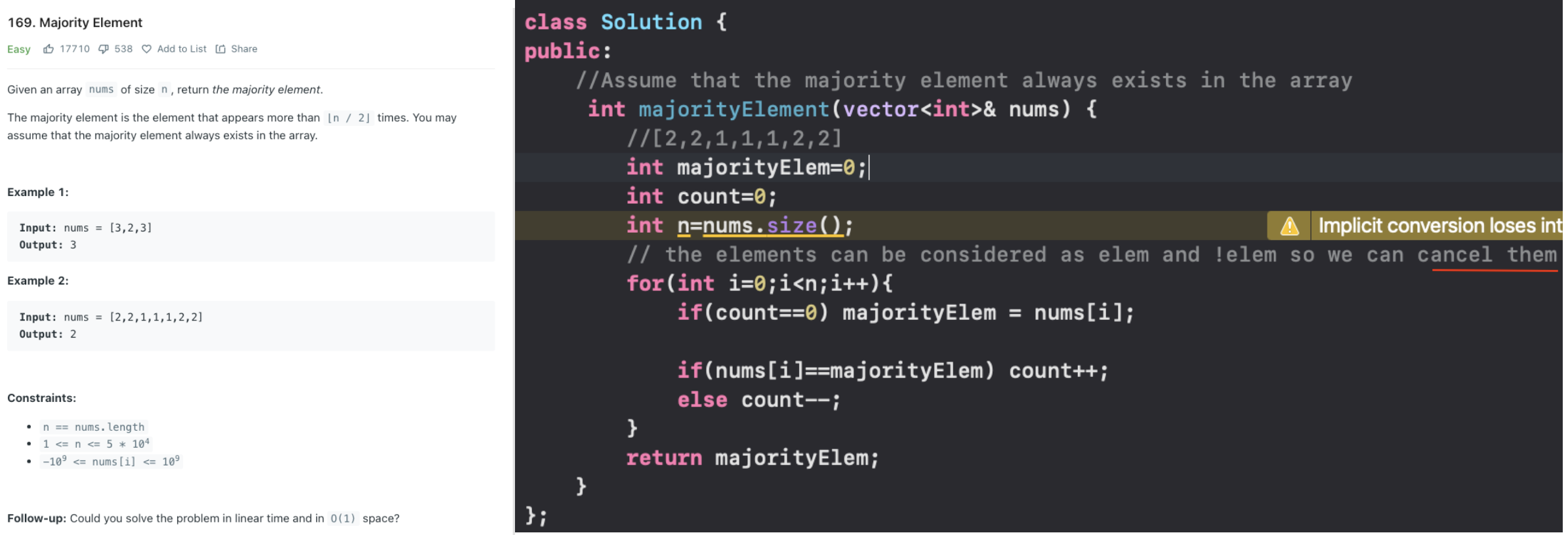
Moore's voting algorithm
Majority Element (n/3 times) 🌟
We will employ the same technique as we did for finding majority element (n/2) but instead of a single counter we will take two
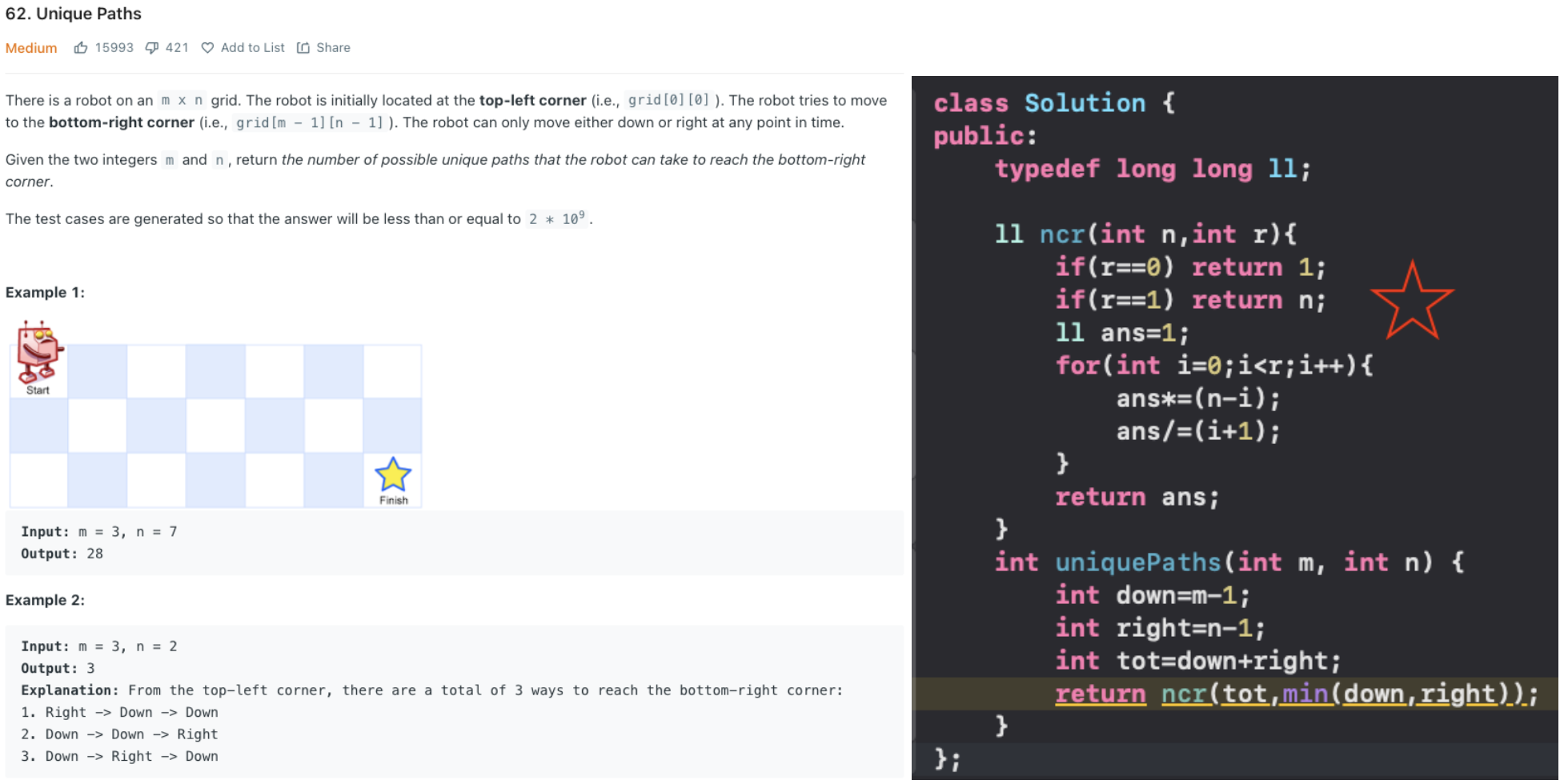
Unique Paths - nCr
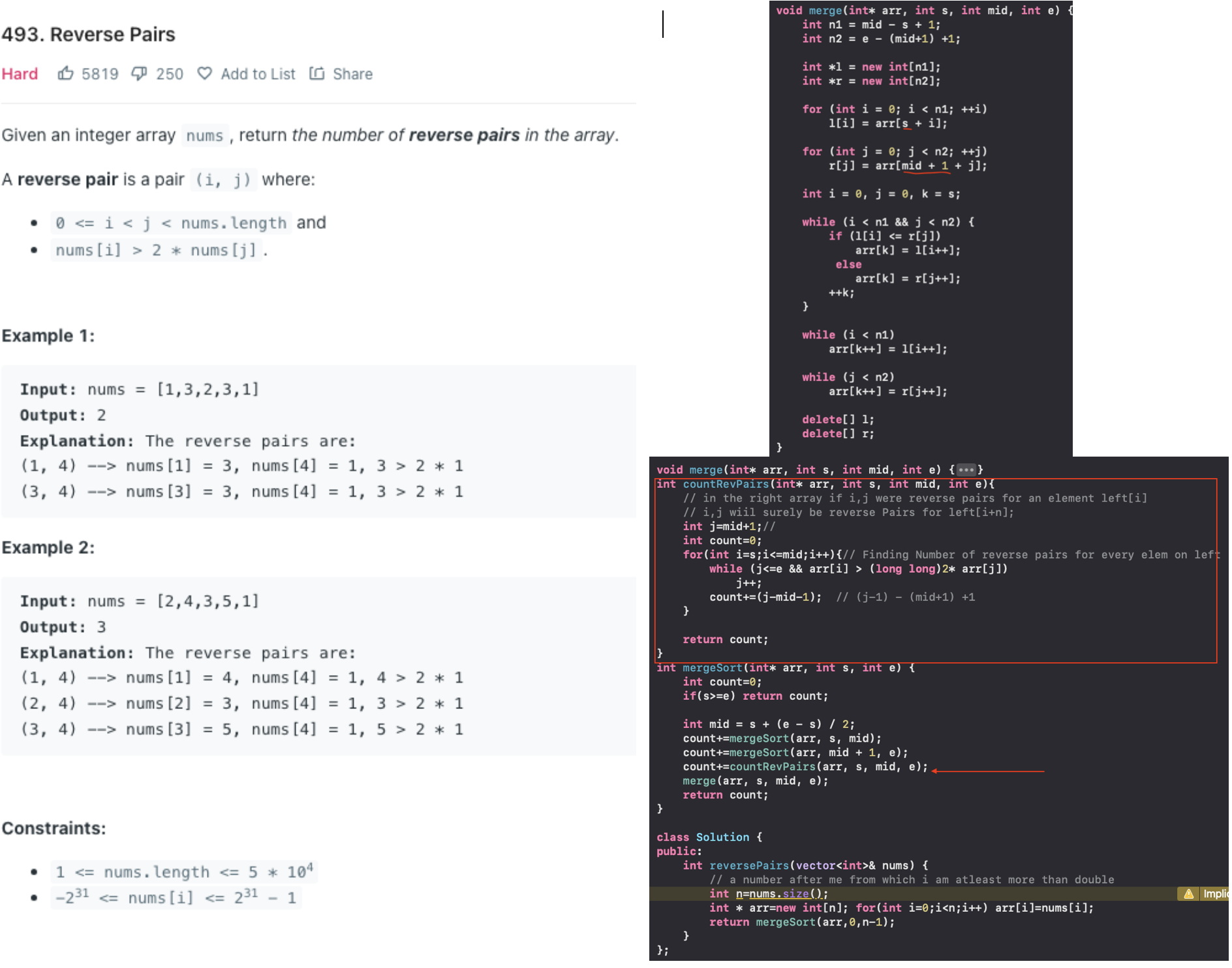
Reverse Pairs
void merge(int* arr, int s, int mid, int e) {
int n1 = mid - s + 1;
int n2 = e - (mid+1) +1;
int *l = new int[n1];
int *r = new int[n2];
for (int i = 0; i < n1; ++i)
l[i] = arr[s + i];
for (int j = 0; j < n2; ++j)
r[j] = arr[mid + 1 + j];
int i = 0, j = 0, k = s;
while (i < n1 && j < n2) {
if (l[i] <= r[j])
arr[k] = l[i++];
else
arr[k] = r[j++];
++k;
}
while (i < n1)
arr[k++] = l[i++];
while (j < n2)
arr[k++] = r[j++];
delete[] l;
delete[] r;
}
int countRevPairs(int* arr, int s, int mid, int e){
// in the right array if i,j were reverse pairs for an element left[i]
// i,j wiil surely be reverse Pairs for left[i+n];
int j=mid+1;//
int count=0;
for(int i=s;i<=mid;i++){// Finding Number of reverse pairs for every elem on left
while (j<=e && arr[i] > (long long)2* arr[j])
j++;
count+=(j-mid-1); // (j-1) - (mid+1) +1
}
return count;
}
int mergeSort(int* arr, int s, int e) {
int count=0;
if(s>=e) return count;
int mid = s + (e - s) / 2;
count+=mergeSort(arr, s, mid);
count+=mergeSort(arr, mid + 1, e);
count+=countRevPairs(arr, s, mid, e);
merge(arr, s, mid, e);
return count;
}
class Solution {
public:
int reversePairs(vector<int>& nums) {
// a number after me from which i am atleast more than double
int n=nums.size();
int * arr=new int[n]; for(int i=0;i<n;i++) arr[i]=nums[i];
return mergeSort(arr,0,n-1);
}
};
2Sum
3 Sum 🌟
Even if we do it via the naive way(cubic), just to ensure unique triplets, we would have to sort the array (we move subsequent pointers to only the next unique numbers) or sort naively
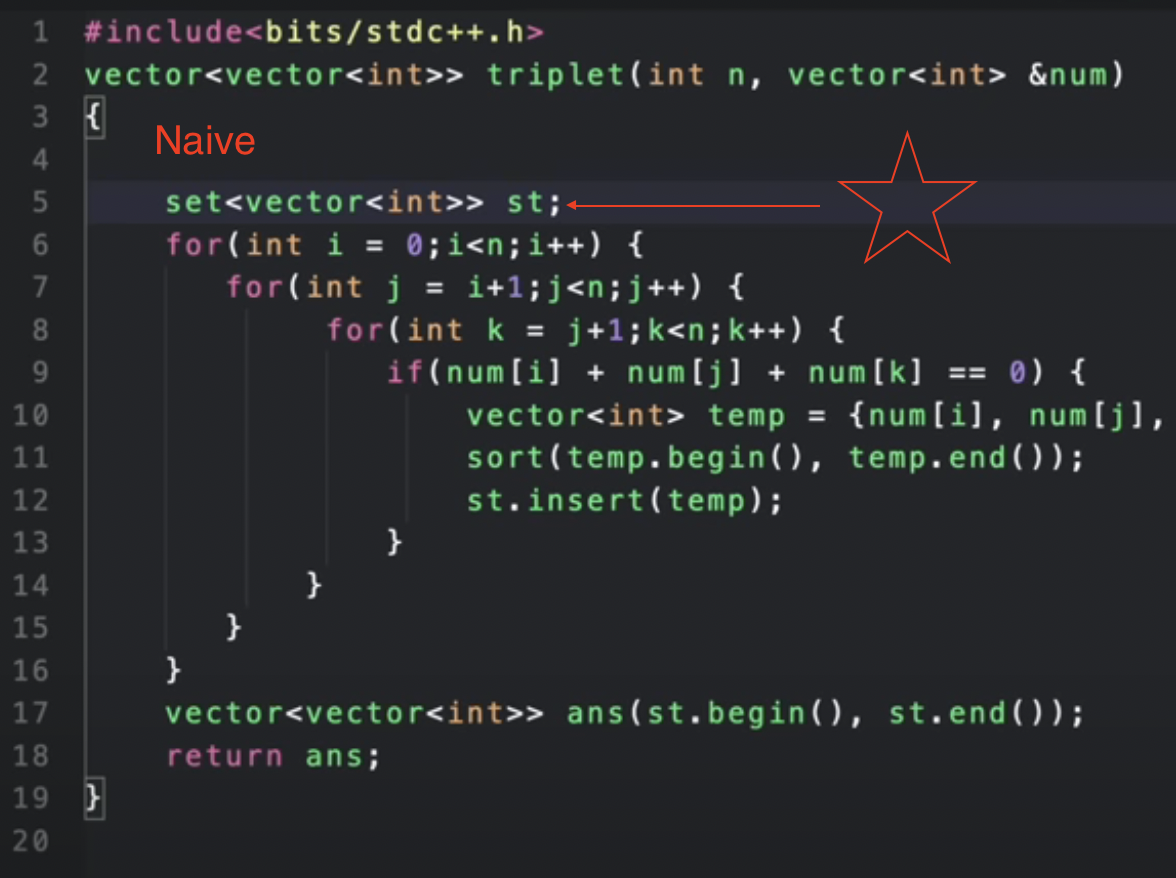
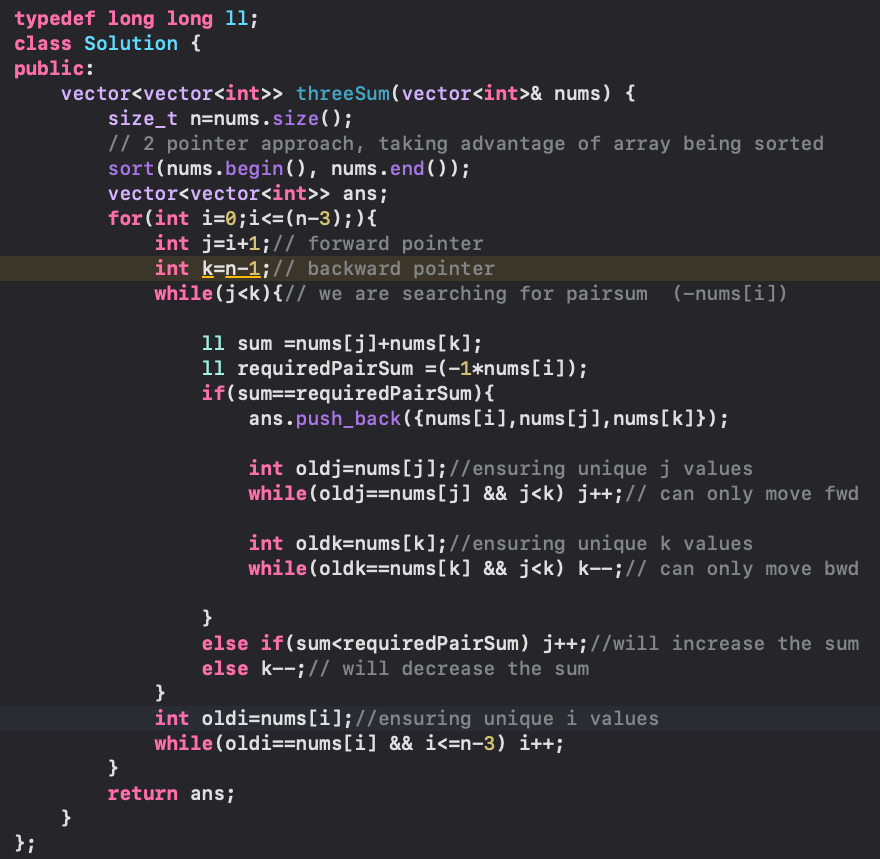
The optimal approach uses 2 pointers giving a quadratic solution
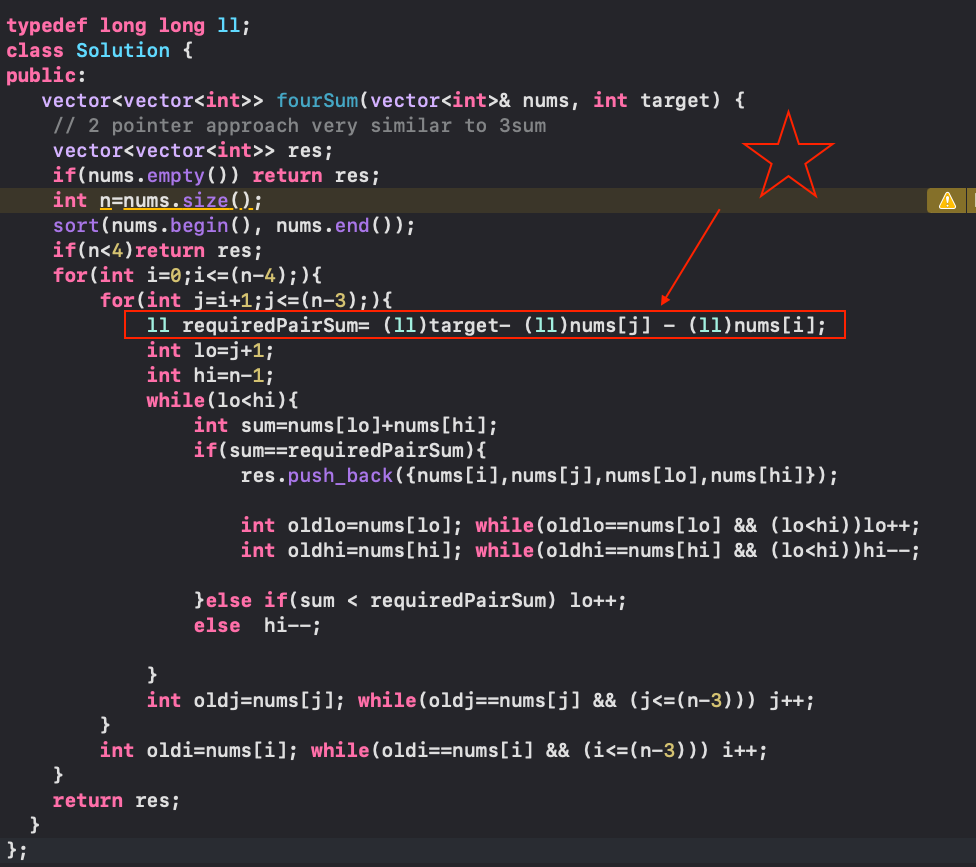
4 Sum 🌟

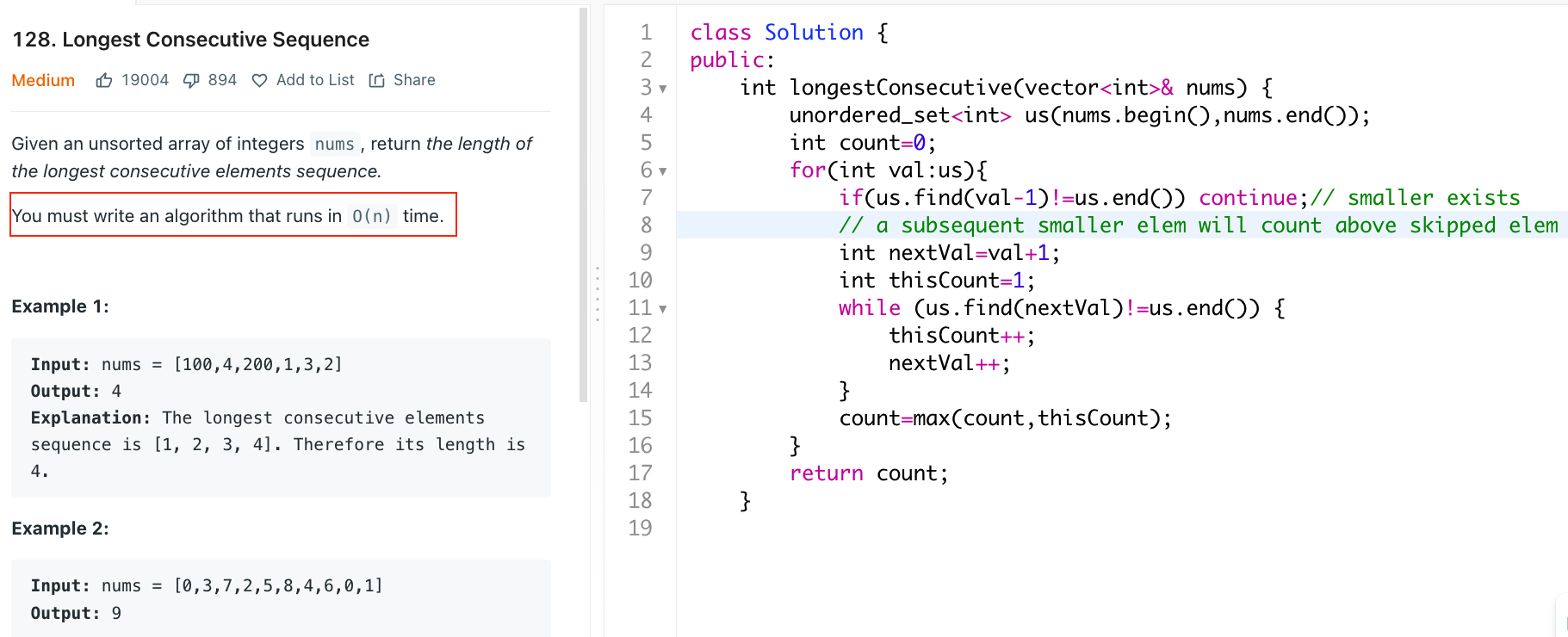
Longest Consecutive Sequence
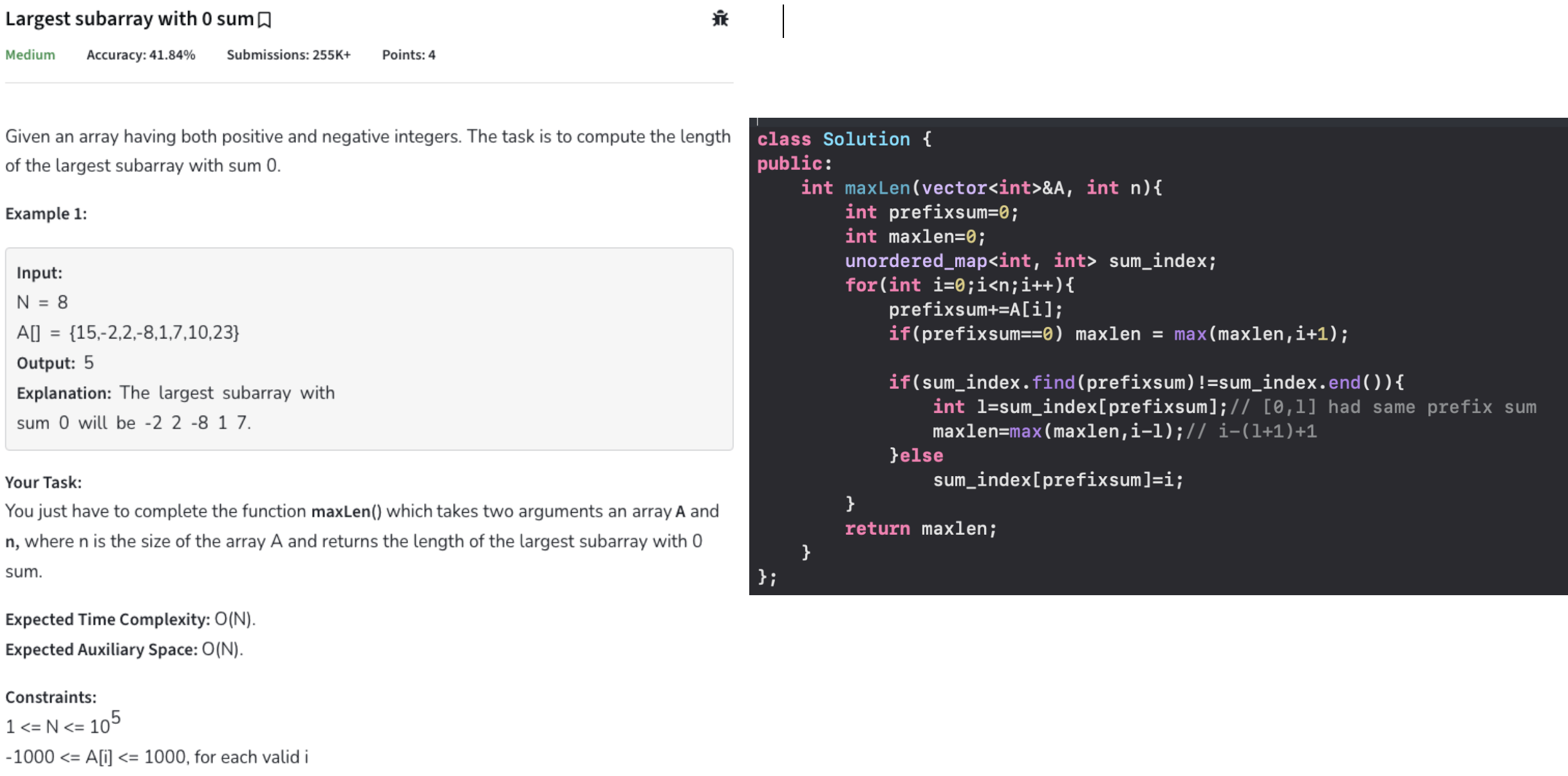
Longest subarray with zero sum (classic Prefix sum problem) 🌟
IDEA : For any array of length n and sum X, if we have sum of ALL its prefix arrays and if sum of any of those is also equal to X , we can be sure there is a suffix array to this prefix array that sums to zero
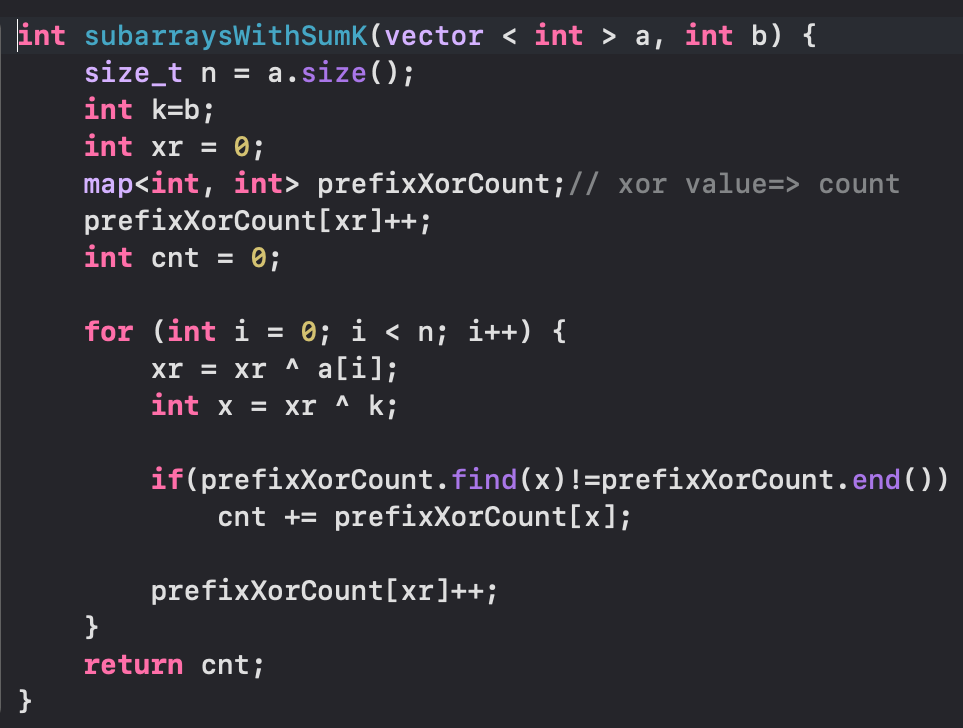
Number of Subarrays with XOR K 🌟

IDEA :
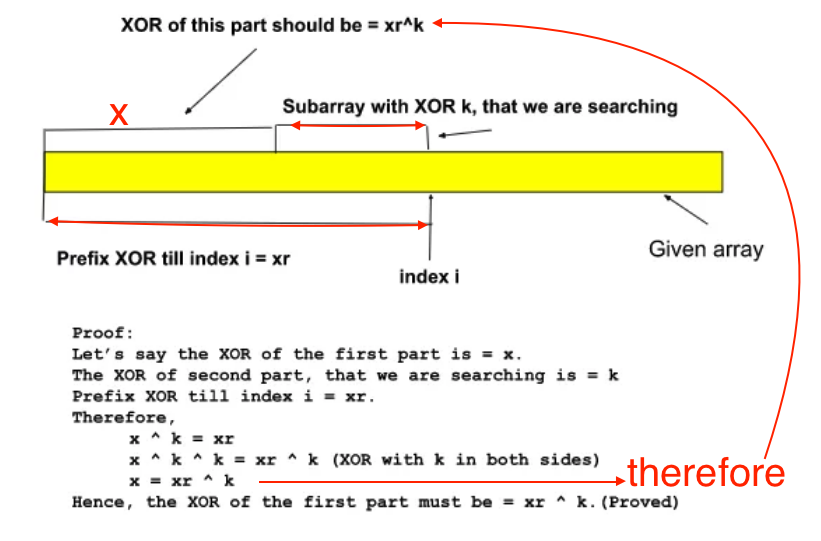
We find the required array via the suffix array if there exists a prefix array which had a xor of xr^k where xr is the current running xor and k is the xor value you want this prefix array to have
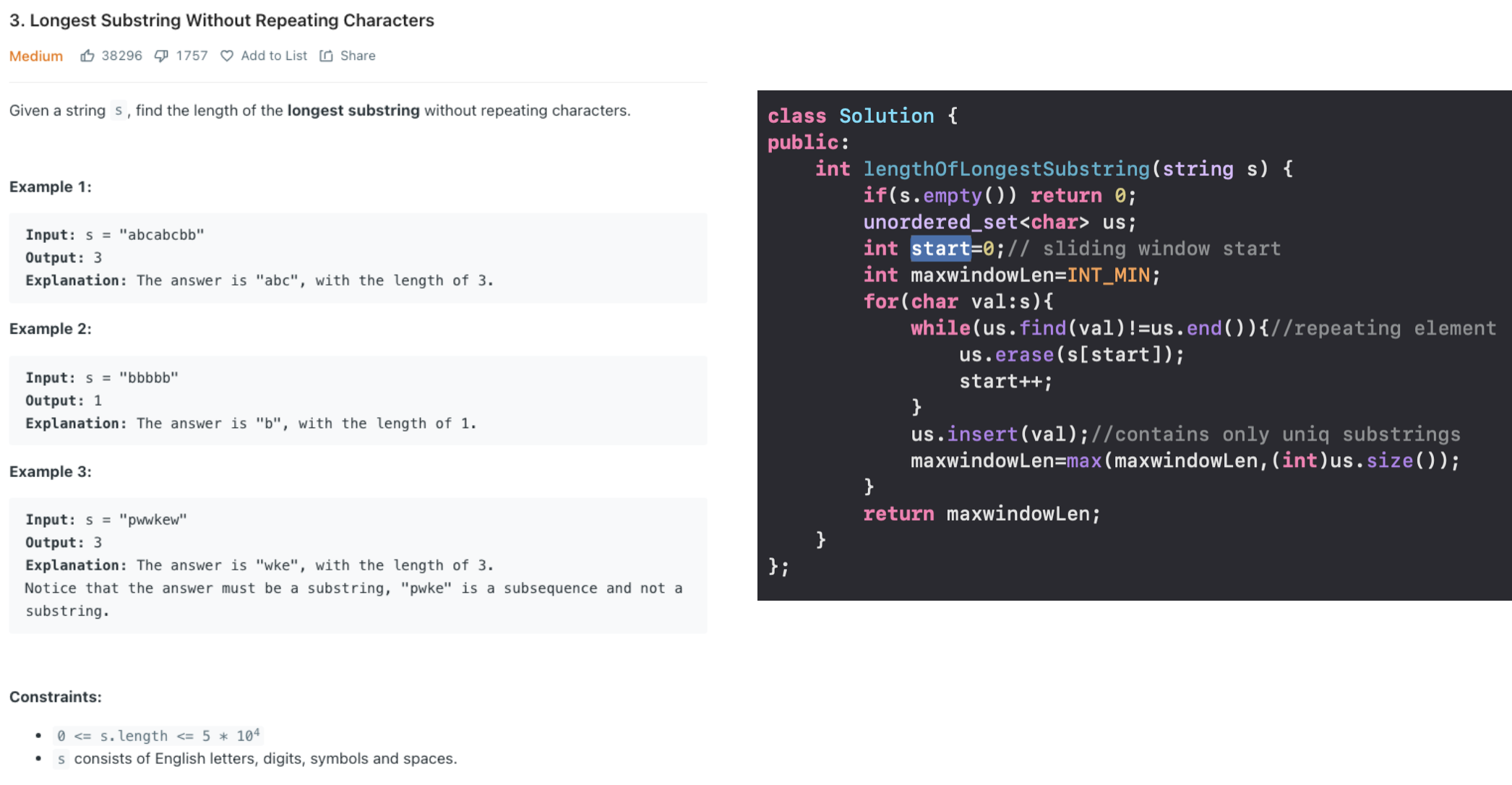
Longest Substring Without Repeating Characters (Classic Sliding window)
Stock Buy and Sell any number of transactions
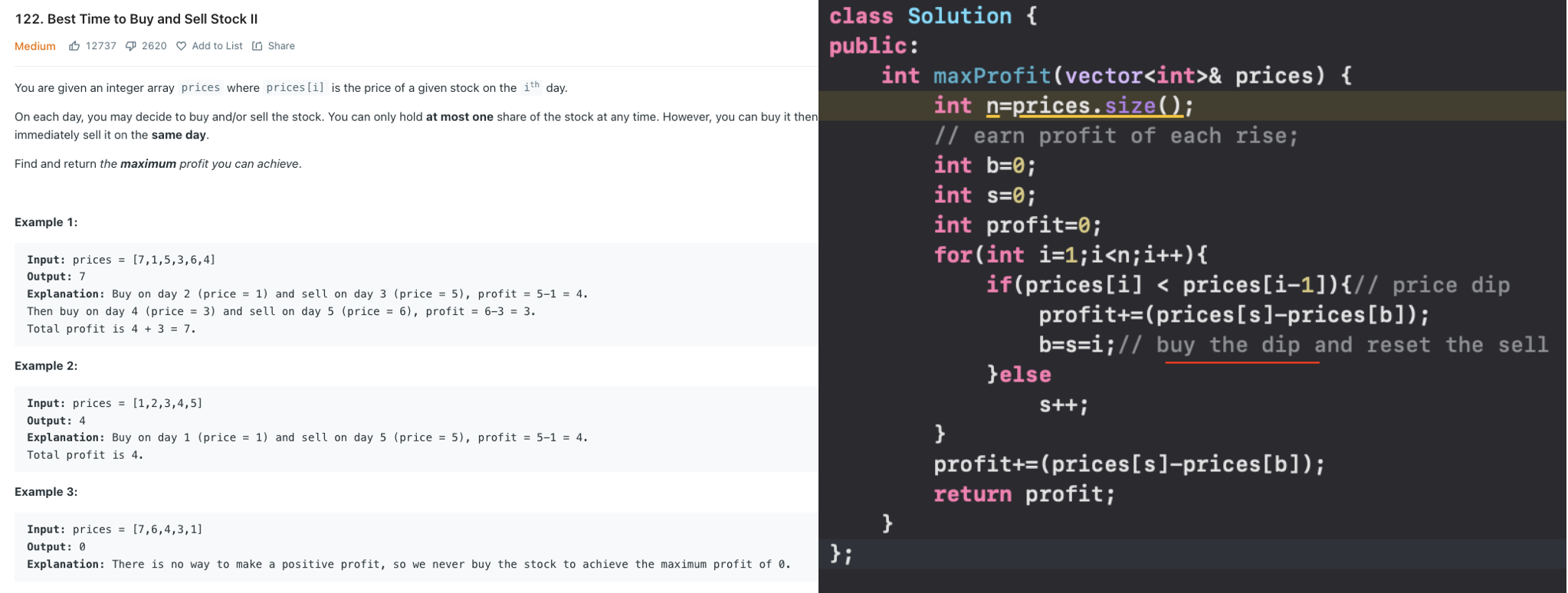
The idea is to accumulate profit on each and every opportunity possible , the above is a two pointer approach , we buy every dip and sell at every peak
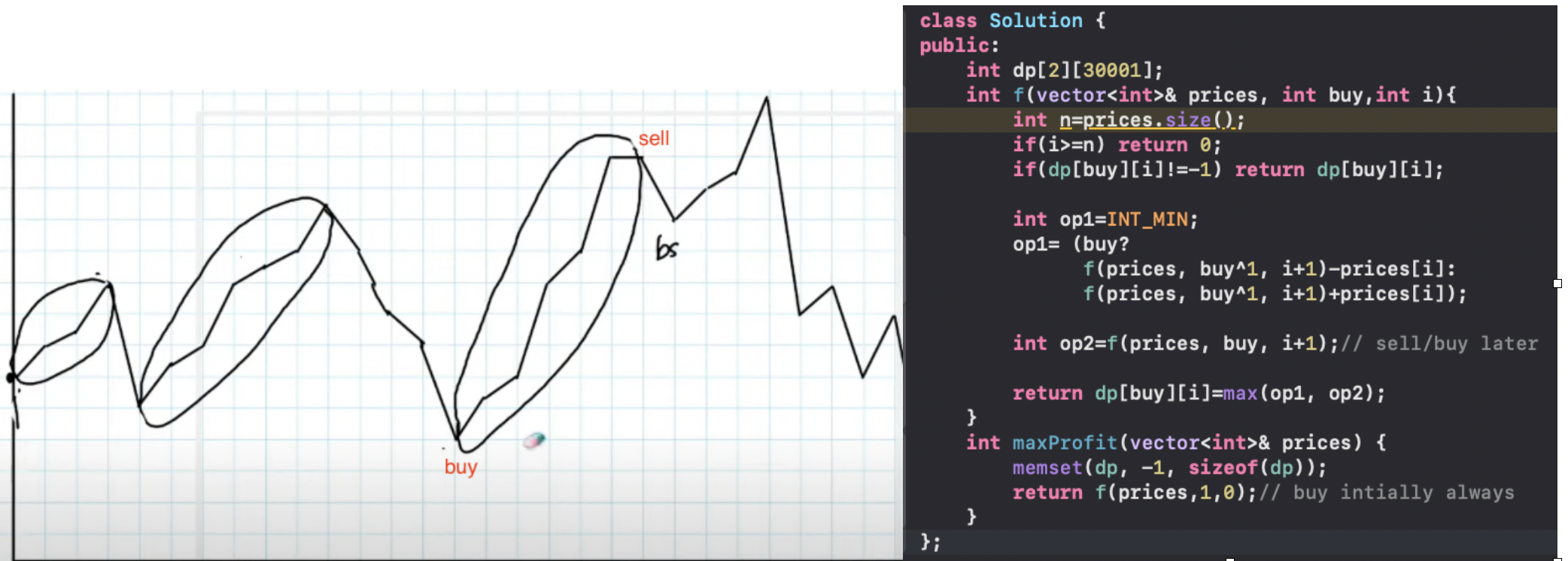
This has a more standard solution using inclusion/exclusion dp , as at each position we have two options either buy/sell or leave it
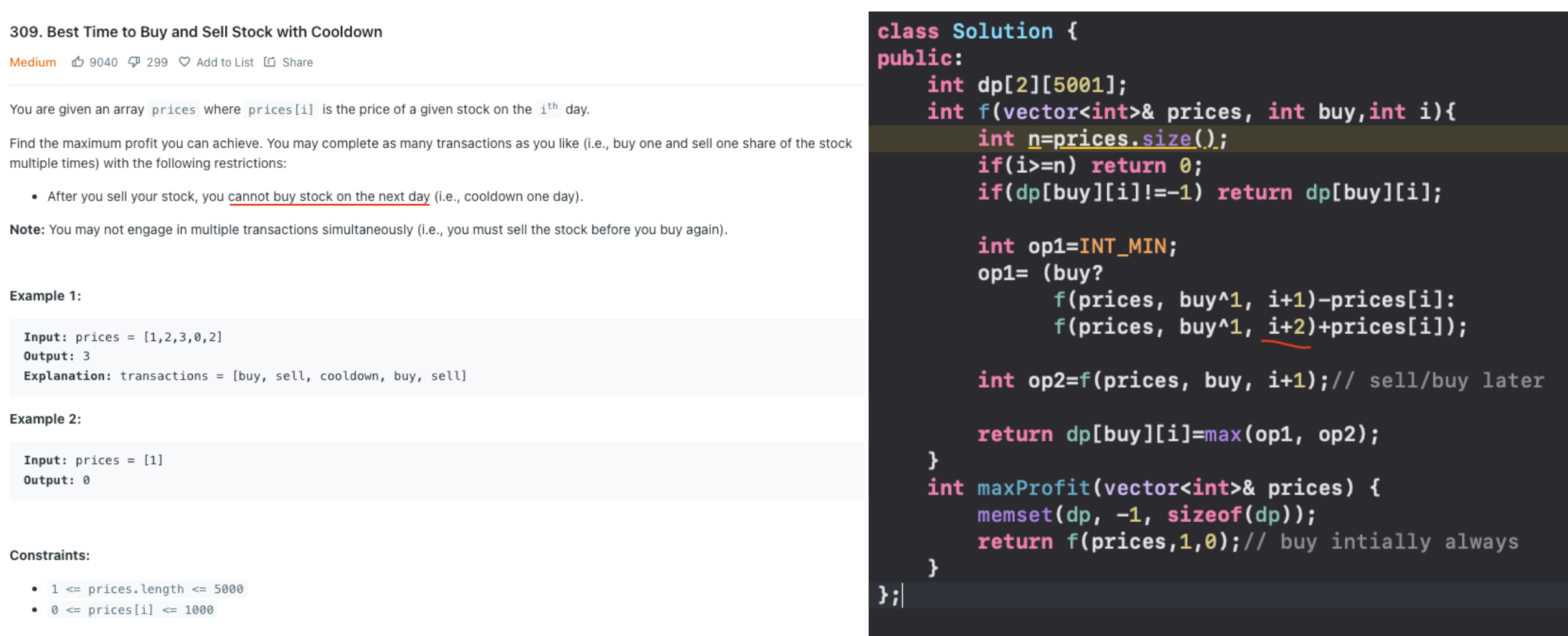
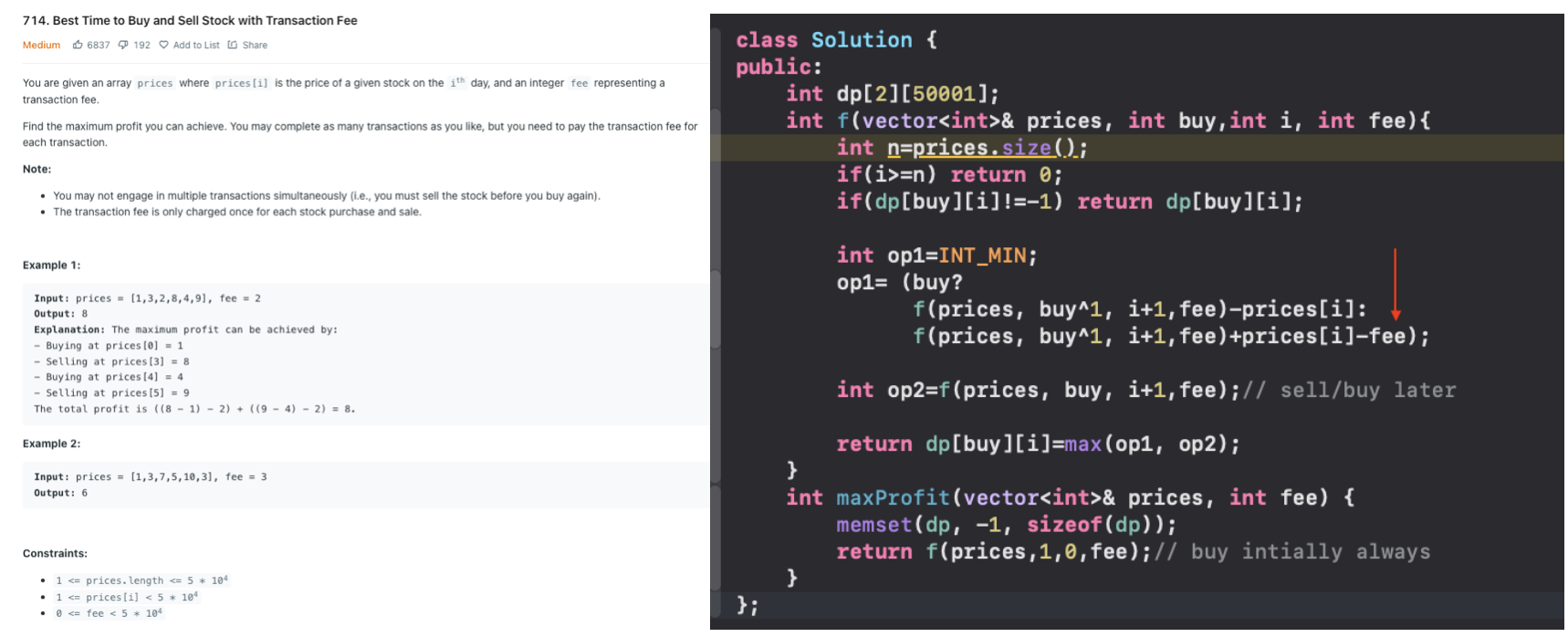
Stock buy and sell with Cooldown / with fee
Stock buy and sell at most 2 transactions allowed (divide and conquer strategy)
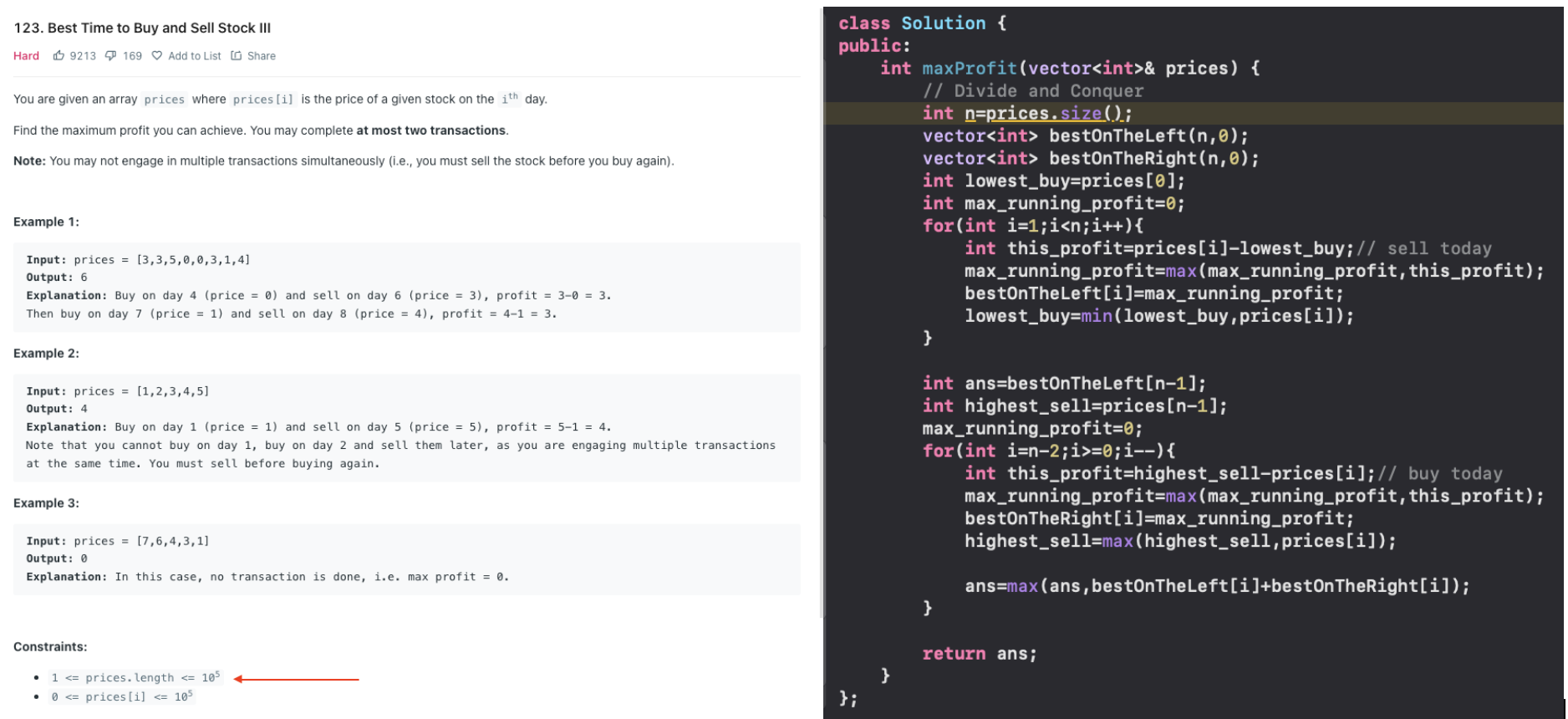
The idea here is to use divide and conquer strategy, we shall divide the problem in two parts
When going forward, we calculate,if selling today is mandatory ,what is the max profit you can make ’before’ this stock
To calc this we find the minima before and buy it then ie “Profit if sold today or before today”
When going backward ,if buying today is mandatory , what is the max profit you can make ‘after’ this stock
To calculate this we find the maxima after and sell it then ie "Profit if sold today or after today"
At every point now we have two non-overlapping transactions
The maximum sum of these arrays denotes the max- achievable profit in two transactions
Best on the left that you can have and Best on the Right you can have.
Stock buy and sell at most k transactions allowed (DP)
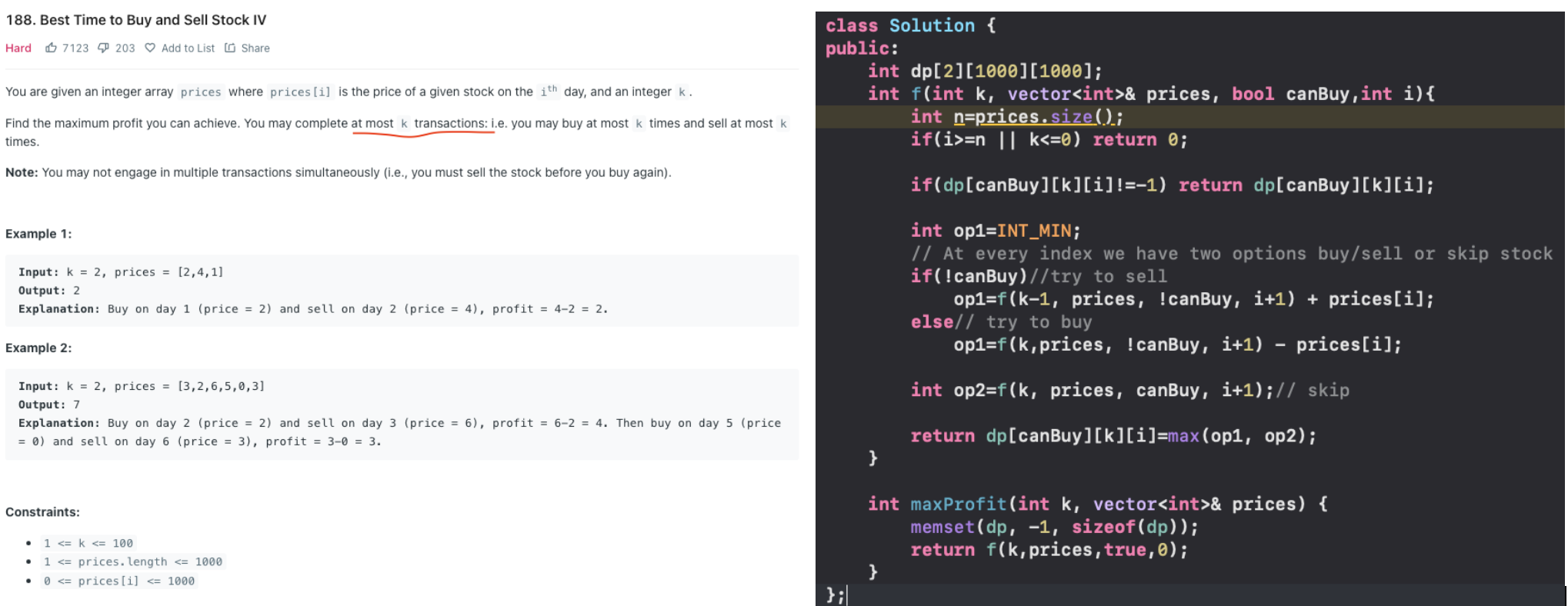
we see inclusion exclusion dp works here
Find First Missing Positive Number 🌟🌟
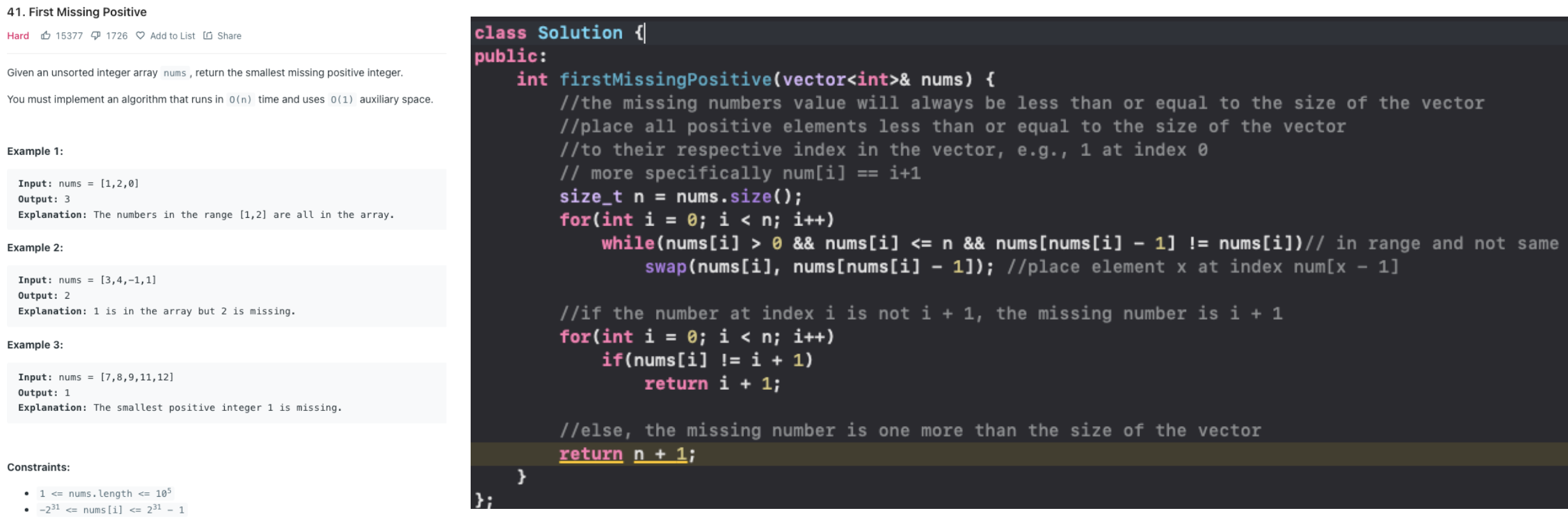
The naive way is to maintain a frequency map from [1,maxElem], then traverse over the map to find the empty slot - but space here is O(nums[i])- this will cause a TLE
But if we see closely if we have n numbers in the array ie we have a n sized array, the missing positive number can always be found between 1 and n+1 , so our space complexity can be reduced to O(n+1) - Our solution becomes bounded [1,N+1]
We intuitively think of an approach similar to Find the duplicate in an array of N+1 integers 🌟
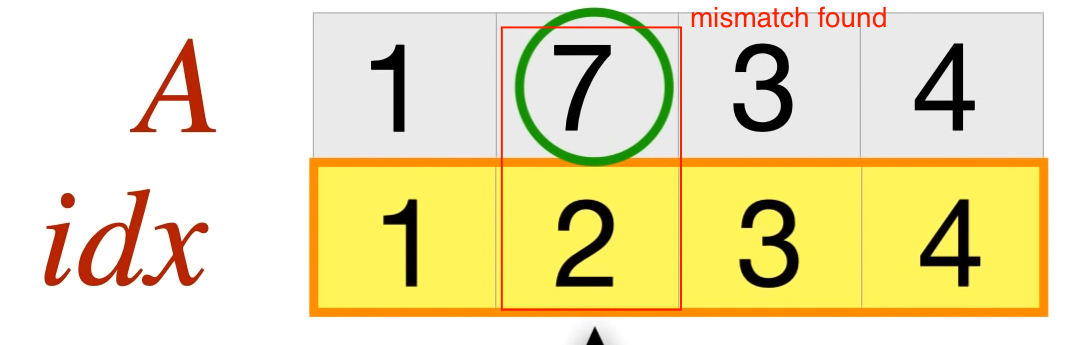
The idea is the place every elemt within the array index range at its correct posisiton
Implement Merge Sort
void merge(int* arr, int s, int mid, int e) {
int n1 = mid - s + 1;
int n2 = e - (mid+1) +1;
int *l = new int[n1];
int *r = new int[n2];
for (int i = 0; i < n1; ++i)
l[i] = arr[s + i];
for (int j = 0; j < n2; ++j)
r[j] = arr[mid + 1 + j];
int i = 0, j = 0, k = s;
while (i < n1 && j < n2) {
if (l[i] <= r[j])
arr[k] = l[i++];
else
arr[k] = r[j++];
++k;
}
while (i < n1)
arr[k++] = l[i++];
while (j < n2)
arr[k++] = r[j++];
delete[] l;
delete[] r;
}
void mergeSort(int* arr, int s, int e) {
if(s>=e) return;
int mid = s + (e - s) / 2;
mergeSort(arr, s, mid);
mergeSort(arr, mid + 1, e);
merge(arr, s, mid, e);
}
Remove Duplicates from Sorted Array
Subscribe to my newsletter
Read articles from Paras kaushik directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Paras kaushik
Paras kaushik
Hello, I'm Paras Kaushik! 👋 I'm a dedicated software engineer based in India, specializing in C++ and proficient in the MERN stack. 🤝 Interested in collaborating on innovative projects that require my technical expertise. 💬 Passionate about participating in discussions related to software architecture and best practices. 📧 Feel free to reach out to me via email: [paraskaushik12@gmail.com] 🔗 Connect with me on LinkedIn: [https://www.linkedin.com/in/the-paras-kaushik/]