How do computers deal with negativity?

This piece is a continuation of my previous post on the Computer Number System.

Signs

For the sake of simplicity, let's suppose all our computers have 8-bit processors.

Consider a decimal, 15. In 8 bits, the binary for 15 is 00001111; there's no doubt about it. But the world of CS is different from that of math. In CS, we have signed and unsigned numbers. A signed number is explicitly stated to be +ve or -ve, whereas an unsigned one always refers to a +ve value. Computers deal with signed values unless compelled to act otherwise. So, the accurate representation of our example is:

$$+15 = (00001111)_2$$

The complement system

To find the binary of a negative number, "math people" came up with the complement system. Consider the decimal, +15. By definition, the 2's complement of 15 is the negative binary of 15.

2's comp = 1's comp + 1

How to find the 1's complement? Just invert the bits! 0 --> 1 and 1 --> 0. In our case, 1's complement of 15 = 11110000. Therefore,

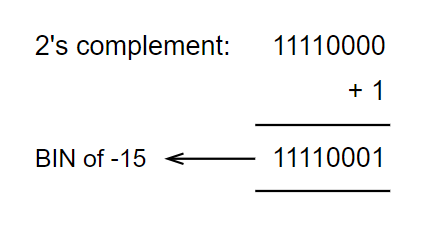
For a moment, ignore the above calculation. Now suppose we're given a binary, 11110001. If we convert it into decimal (following the usual method), we get 241. But the complement system claims, it's the binary for -15.

A contradiction?!

Let's get clarity, shall we?

In a binary, the leading bit is for magnitude (sign): 0 is (+) and 1 is (-). For instance, consider 10001010. Say, we want its corresponding decimal.

Wrong method: Leading bit is 1, which means the dec is -ve. Then, converting the remaining bits as usual gives 10. So, is the answer -10? It's not, because the complement system shows that the negative binary for 10 is 11110110.

Correct method: Find the 2's complement of the given binary.

Now converting this binary gives the correct answer. Thus, the required dec is: -118. Let's cross-verify.

Now consider the binary, 01010101.

Here, the leading bit is 0, which implies the dec is +ve. In such a case, the 2's comp is not needed, we can just convert the binary using the usual method of powers of 2. But if we still go ahead and use the above method, we'll end up with the -ve version of the given binary.

Hence, 01010101 = +85

Bitwise NOT

In a programming language, tilde (~) is referred to as the Bitwise NOT operator. The following JS console session shows '~' in action:

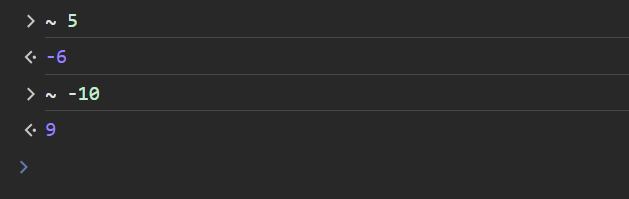
At the processor level, '~' operator flips every bit of the operand, essentially generating its 1's complement. Consider +5 in 8 bits: 0000 0101. Upon flipping, we have

1111 1010 --> Binary for ~5

But the output (as shown above) is a decimal; hence, the above binary must be converted.

Here, the leading bit is 1, implying a '-' sign. Next, we find its 2's complement, and then convert it.

2's comp = 1's comp + 1
         = 00000101 + 1 = 0000110 --> 6

Thus, the output is -6

Now consider -10 in 8 bits: 1111 0110 (2's comp of +10). In this case, too, applying '~', flips the bits.

0000 1001 --> Binary for ~ -10

Since the leading bit is 0, its equivalent decimal is +ve, allowing us to get the decimal directly:

0000 1001 = 2^3 + 1 = 9

Hence, the output is +9

** There's a mathematical equivalent to the above bit-level operation. The expression is:

$$\sim n = -(n + 1)$$

Check:
~5 = -(5 + 1) = -6
~(-10) = -(-10 + 1) = 9

Bonus: Encode it!

Computers don't understand anything except strings of 0's and 1's. So, we have encoding systems in place to convert characters from our languages into bits. ASCII and Unicode are two such systems.

ASCII (American Standard Code for Information Interchange), first published in 1963, is the most common format for encoding text in computers and on the internet. It comprises unique values for 128 characters - alphabets (A-Z and a-z), numeric digits (0-9), and some special and non-printable characters. Each character is encoded using 8 bits.

Here's an ASCII table

There's a major drawback to the ASCII standard: 255 is the maximum value that can be represented using 8 bits, which means there are 256 different ASCII characters only. That number is not enough for a comprehensive encoding of text in world-languages, including English.

Unicode takes care of the issue by extending the character set, vastly. It encodes a huge number of characters - Greek letters, math symbols, emojis, and more. Essentially,

$$\text{ASCII } \subset \text{ Unicode}$$

---

Thank You!

To support me, plz like and share 😊