Join Algorithms - Nested Loop Join

Introduction

This article offers an insightful exploration into the inner workings of the Nested Loop Join algorithm, understanding its components in query plans. It delves into a detailed cost analysis and examines its performance across various scenarios. The piece clarifies why nested loop joins can be advantageous in certain situations, yet less efficient in others, and discusses the conditions under which an optimizer might choose to use this algorithm.

Nested Loop Join Algorithm

the Nested Loop Join is a fundamental database algorithm used in joining between two table on a specified join condition in relational database. It operates by iterating over each row of one table (the outer loop) and for each row, scanning through the second table (the inner loop) to find matching rows based on the join condition and effect index on the join attribute in the inner table

Algorithm explanation

Assume Table R with M pages and m tuples, and Table S with N pages and n tuples

foreach tuple r in Table R:
    foreach tuple s in Index(Table S, where ri = sj):
        if r and s match based on the join condition:
            emit (add to result set) the combined tuple

Outer Table Iteration:

The algorithm starts by iterating over each tuple r in the outer table, Table R.
Index Lookup for Matching Tuples:

For every tuple r in Table R, the algorithm then performs an index lookup on Table S. The goal is to find tuples s in Table S that match the join condition with tuple r from Table R.
Match Identification and Tuple Combination:

When the algorithm identifies a match – that is, when it finds a tuple s in Table S that meets the join condition with tuple r from Table R – it combines these tuples to form a single joined tuple.
The Power of Indexing in Nested Loop Joins:

The Index Nested Loop Join algorithm's efficiency is rooted in its use of the index on the inner table (Table S). This index, central to the algorithm, enables it to rapidly locate tuples s in Table S that satisfy the join condition with tuples r from the outer table (Table R).This setup allows the algorithm to perform targeted lookups instead of full table scans of Table S, dramatically reducing the I/O cost happen in full table scans.

PostgreSQL Example With explaining Nested loop Join Query Plan

Assume we have
- orders table: 15,000 rows
- customers table: 12,000 rows
- There is a one-to-many relationship between customers and orders each customer has many orders.
- The customers table has a primary key index on u.id, ensuring efficient lookups.
Query to return the customer name for each order

SELECT o.id, c.name
FROM orders as o
JOIN customers as c ON o.customer_id = c.id;

Nested Loop (cost=0.00..30000.00 rows=15000 width=1024) (actual time=0.026..250.123 rows=15000 loops=1)
-> Seq Scan on orders o (cost=0.00..1500.00 rows=15000 width=524) (actual time=0.017..125.456 rows=15000 loops=1)
-> Index Scan using customers_pkey on customers u (cost=0.01..1.00 rows=1 width=500) (actual time=0.005..0.005 rows=1 loops=15000)
   Index Cond: (id = o.customer_id)
Planning Time: 0.500 ms
Execution Time: 250.789 ms

Explaining the Nested Loop Join Query Plan
- Seq Scan on orders (Outer Table):
  - Role as Outer Loop: In the Nested Loop Join, the orders table serves as the outer loop. This sequential scan processes each row in the orders table one after the other.
  - Total Rows Processed: For this Seq Scan, the total number of rows in the orders table that the database iterates through is 15,000 (rows=15000).
  - The Width of rows : The width of 524 bytes indicates the average size of each row in the orders table as estimated by the database. This size is important for understanding the data throughput and memory usage of the query. Larger rows mean more data to process and transfer, which can impact performance.
  - Cost Estimate:
    - The start-up cost (the first number) represents the resource cost before the database can start returning the first row. This includes costs like loading indexes or initial table access.
    - The total cost (the second number) is an estimate of the cost to complete the scan of all rows. This is a cumulative cost, including the start-up cost.
- Index Scan on customers (Inner Table):
  - Triggered by Outer Loop: Each row retrieved from the orders table during the Seq Scan prompts an Index Scan on the customers table.
  - Efficient Matching Using Index: The Index Scan on the customers table utilizes the primary key index (customers_pkey) to rapidly locate the matching user for each order.
  - Join Condition: The Index Scan is guided by the join condition id = o.customer_id, which efficiently matches each order to its corresponding customer.
  - One Match per Row: The rows=1 notation in the index scan suggests that for each row from orders, the database expects to find exactly one matching row in customers.
  - Cost in Index Scan component :
    - The cost range 0.01..1.00 in the index scan represents the average estimated cost for a single lookup.
    - The 0.01 indicates the initial start-up cost, which is the overhead for beginning the index scan operation.
    - The 1.00 is the estimated total cost for completing one lookup. This includes the initial start-up cost and the cost of actually performing the scan to find a matching row.

Algorithm cost analysis

The Index Nested Loop Join algorithm works by systematically pairing rows from an outer table with those of an inner table, using an index to improve the efficiency of the search. The cost formula M + (m * C) reflects the detailed steps of this process:

Reading Outer Table Pages (M):

The algorithm starts by sequentially reading each page from the outer table R. The cost M reflects the I/O operations for accessing these pages from disk storage. Here, the focus is on I/O costs, as they are generally more significant than computational costs in this context.,
Loading Pages into Memory: Each page retrieved from the disk is loaded into the database's memory. This step is crucial because the actual comparison operations for the join condition can only be performed on data in memory, not directly on disk.
Row-by-Row Index Lookup (m * C): Within each page loaded in the memory , for every row r, the algorithm performs an index lookup in the inner table S. This is where the index on S comes into play, allowing for a quick search to find any matching row s that satisfies the join condition (typically something like r.id = s.id).
Constant Cost Per Lookup (C): Each of these index lookups incurs a fixed cost C. This cost encapsulates the operations needed to traverse the index structure (like a B-tree) and locate the matching row in table S. The index is designed to make this process much faster than scanning every row of S
Iterative Process: After the algorithm has processed all rows on a page from table R, it fetches the next page and repeats the process. This loop continues until all pages of the outer table have been read and all potential matches have been found.
Total Cost (M + (m * C)): The total cost combines the page access cost (M) with the cumulative cost of all the index lookups performed (m * C). M represents the number of page reads necessary, and m * C represents the total cost of index lookups across all rows in the outer table.
Formula primary Focus on I/O Costs and ignore most of computational costs: the formula considers only I/O cost and ignore most of computational costs,this is because, in database operations, the time required for disk I/O operations is substantially greater than that for computational tasks. While computational aspects like evaluating join conditions or navigating data structures are important, they are relatively minor in terms of execution time compared to the latency involved in disk access. As a result, the formula focuses more on the I/O operations, which are the primary performance bottleneck in database query processing

When the Optimizer Prefers Nested Loop Joins

selectivity is a crucial factor that greatly influences the method's efficiency. Selectivity, in database terms, refers to the proportion of rows in the inner table of a join operation that satisfy the join condition with the outer table
Understanding Selectivity
- Selectivity refers to the fraction of rows in a table that meet the join condition. A selectivity near 0 in the below graph means few rows meet the condition, while a selectivity near 1 means most rows meet the condition.

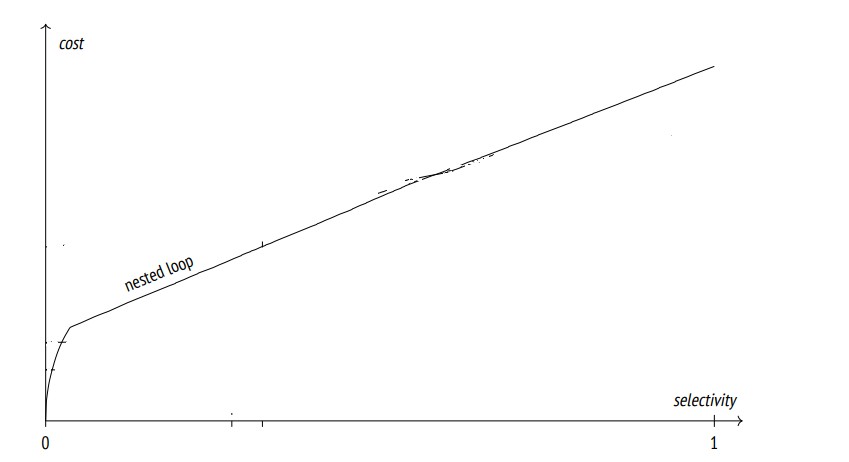
Nested Loop Join Efficiency Based on Selectivity
- Low Selectivity (No Rows Match):
  - At low selectivity (near 0 on the horizontal axis), the graph shows a high initial cost for the nested loop join. This is because the likelihood of finding matching rows in the inner table for each row in the outer table is low.
  - The nested loop join is less efficient here because it involves a lot of searching (or "looping") without finding many results. It's akin to looking for a needle in a haystack; you spend a lot of time searching but find very few or no needles .
  - a selectivity of exactly zero is quite rare in practical scenarios; usually, there is at least some non-zero chance of finding matching rows.
- Increasing Selectivity (Moderate Rows Matches):
  - As selectivity increases, the graph flattens out, indicating that the cost of the nested loop join does not increase as much with each additional row.
  - This flattening occurs because the nested loop join can utilize index access on the inner table. When more rows in the outer table are likely to find matching rows in the inner table, index lookups become much quicker than scanning the entire inner table.
  - In this situation, a reasonable number of rows meet the join condition. The algorithm can effectively use indexes to find these matches quickly, without the need to examine every row.
  - This balance ensures that the algorithm doesn't waste time on excessive searching, nor does it become bogged down by too many matches. It's similar to flipping through a book where the word you're looking for appears regularly but not on every page.
  - During this phase, the nested loop join is efficient and well-suited for the task, especially when you need to retrieve results quickly without scanning entire tables.
- High Selectivity (Most Rows Match):
  - At high selectivity (approaching 1), the graph shows the cost beginning to rise linearly again. This happens because, as the proportion of matching rows increases, the benefit of using the index for each lookup diminishes.
  - When most or all rows match, the database might opt to perform a full scan of the outer table instead of using the index for each row. At this point, the overhead of index lookups may be greater than the cost of a full scan, and that's let the optimizer to choose hash join or merge join algorithm
  - The nested loop join becomes less efficient compared to other join methods that can handle this case more effectively, like hash joins or merge joins.
- Key Point Selectivity is moderate : The nested loop join is most efficient when selectivity is not too high, but at a moderate level. When selectivity is extreme (very high match), the time and resources spent in finding or dealing with many matches can make the nested loop join less effective compared to other join methods. The choice of the join method should thus be informed by the expected selectivity of the join condition.
High Selectivity Query Example Leading the Optimizer to Switch to Hash Join
- Assume we have
  - employees table: 10,000 rows
  - timesheets table: 10,000,000 rows
  - timesheets table are used to track an employee's working hours for each day
  - There is a one-to-many relationship between employees and timesheets each employee has many timesheets.
  - each tuple in employee table has 1,000 tuple in timesheets
  - The timesheets table index on timesheets.employee_id and no index exists on employees.employee_id for simplicity .
- Lets have query to find all worked hours for each day for the employees
  - ```
                SET enable_hashjoin = OFF;
                SET enable_mergejoin = OFF;
                EXPLAIN (ANALYZE) SELECT e.employee_id, e.name, t.day, t.hours_worked 
                FROM employees e 
                JOIN timesheets t ON e.employee_id = t.employee_id;
```
- Disable hash and merge join algorithms : To demonstrate the use of nested loop joins in this specific query scenario, we disable the hash and merge join algorithms using the commands SET enable_hashjoin = OFF; and SET enable_mergejoin = OFF;. This action compels the database's query optimizer to resort to nested loop joins, which is crucial for our analysis since, under normal circumstances, the optimizer would likely choose the more efficient hash or merge join methods for this particular query
- Explain Query Plan
- ```
              Nested Loop  (cost=0.25..40000.75 rows=10000000 width=150) (actual time=0.030..8000.000 rows=10000000 loops=1)
                ->  Seq Scan on employees e  (cost=0.00..300.00 rows=10000 width=50) (actual time=0.020..200.000 rows=
               loops=1)
                ->  Index Scan using timesheets_employee_id_idx on timesheets t  (cost=0.25..3.75 rows=1000 width=100) (actual time=0.020..0.800 rows=1000 loops=10000)
                      Index Cond: (e.employee_id = t.employee_id)
              Planning Time: 0.500 ms
              Execution Time: 8000.000 ms
```
  1. Sequential Scan on employees:
    - The database performs a full scan (Seq Scan) of the employees table.
    - It processes 10,000 rows (the total number of employees).
    - This step is relatively fast (200 milliseconds).
  2. Index Scan on timesheets:
    - For each of the 10,000 employee rows, an index scan is performed on the timesheets table.
    - Each employee has about 1,000 corresponding timesheet entries (rows=1000), leading to a very high number of total operations (10,000 employees × 1,000 timesheets each).
  3. Why It's Inefficient:
    - High Selectivity: The scenario represents high selectivity, where nearly every row from the outer table (employees) has a large number of matching rows in the inner table (timesheets).
    - Cost of high Selectivity :
      - The plan shows an estimated cost of 0.25..3.75 for each index scan on timesheets. While this cost might seem low for a single operation, it becomes substantial when multiplied by the number of operations.
      - Total Cost for Index Scans: With 10,000 employees and each requiring 1,000 index scans, the cumulative cost of these scans is significant. Mathematically, this can be approximated as 10,000 (employees) × 3.75 (maximum cost per scan) = 37,500. This number represents the total cost of all index scans in the nested loop operation which is 93.75% of the overall cost!.
    - Comparison with Sequential Scan
      - This means that in certain cases, especially with high selectivity, the presumed efficiency of index scans over sequential scans may diminish. The overall cost of processing such a high volume of index scans can become comparable to, or even more than, what a full table scan would require.
      - In a scenario like ours, where each employee has about 1,000 timesheet entries, the database must perform an index scan for each of these entries. This translates to millions of index scans, the cumulative cost of these index scans , for each row lookup in the nested loop join, the repeated index scans incrementally add to the overall cost, potentially making it more and more expensive than a full table scan, which alternative algorithms like hash or merge joins should be more efficient . (Will be explained in next two articles isa)

Lets enable hash and merge join algorithm to see the optimal algorithm the optimizer will use

              SET enable_hashjoin = on;
              SET enable_mergejoin = on;
              EXPLAIN (ANALYZE) SELECT e.employee_id, e.name, t.day, t.hours_worked 
              FROM employees e 
              JOIN timesheets t ON e.employee_id = t.employee_id;

              Hash Join  (cost=500.00..5000.00 rows=10000000 width=150) (actual time=0.100..1500.000 rows=10000000 loops=1)
                Hash Cond: (e.employee_id = t.employee_id)
                ->  Seq Scan on timesheets t  (cost=0.00..500.00 rows=10000000 width=100) (actual time=0.050..700.000 rows=10000000 loops=1)
                ->  Hash  (cost=300.00..300.00 rows=10000 width=50) (actual time=0.050..0.050 rows=10000 loops=1)
                      ->  Seq Scan on employees e  (cost=0.00..300.00 rows=10000 width=50) (actual time=0.020..200.000 rows=10000 loops=1)
              Planning Time: 0.200 ms
              Execution Time: 1500.000 ms

Optimizer choose hash table over nested loop algorithm : optimizer selects a hash join primarily for its efficiency in rapidly matching rows between large datasets, especially under high selectivity conditions. By creating a hash table for the smaller table (employees), the hash join enables quick lookups for matching rows in the larger table (timesheets), significantly reducing the time complexity compared to a nested loop join. This method is particularly effective in large datasets where most rows in one table have corresponding matches in the other, as it avoids the intensive row-by-row comparisons and minimizes disk I/O, making it a more optimal (Will Explain hash join in details in next article Isa)

Summary

In this overview, we dissect the Nested Loop Join algorithm, revealing its step-by-step process of iterating over each row in one table (outer loop) and scanning the second table (inner loop) for matching rows using index. We delve into its cost formula M + (m * C) primary Focus on I/O Costs and ignore most of computational costs , highlighting how it quantifies the algorithm's efficiency when Selectivity is moderate. Finally, we discuss how high selectivity—when most rows find matches—can lead to bad performance potentially making it more and more expensive than a full table scan , often prompting the optimizer to switch to more suitable methods like hash or merge joins.

Query Execution Part 1: Join Algorithms - Nested Loop Join

Table of contents