Coding a Pascal's Triangle Best Explanation
 Abhik Bhattacharya
Abhik Bhattacharya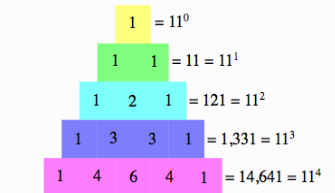
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
That's how a pascal triangle looks like...
Understanding the row structure
Rows start from 1 , so row 1 is 1 , row 2 is 11 , row 3 is 121 & so on....
At first glance it looks like first row is 1, then every row is 11 multiplied to the previous row. 1 X 11 = 11 , 11 X 11 = 121 , 121 X 11 = 1331...
Another way of looking at it is : every row begins & ends with 1 but the middle elements are sum of previous rows 2 columns just above the current number. Example :
row 4 elements are 1331, row 5 elements are 14641.
row 5 middle elements : 4 is sum of (1+3) , 6 is sum of (3+3) , 4 is sum of (3+1).
(See the triangle to understand more)3rd way to look at it is : binomial coefficients. Each element is a binomial coefficient of binomial theorem. (More on this later...)
How to find each element in a row
There is a simple formula for that. The first element in each row is 1. All elements after 1st element in a particular row are calculated using the below formula :
$$element = \frac{previous\space element \times (row -col)}{col}$$
Dry Run
Row 1 :

Row 2 :
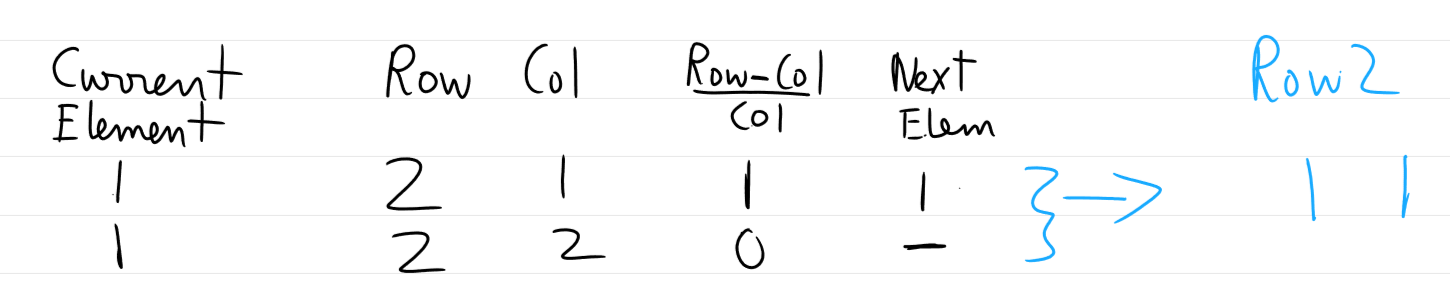
Row 3 :
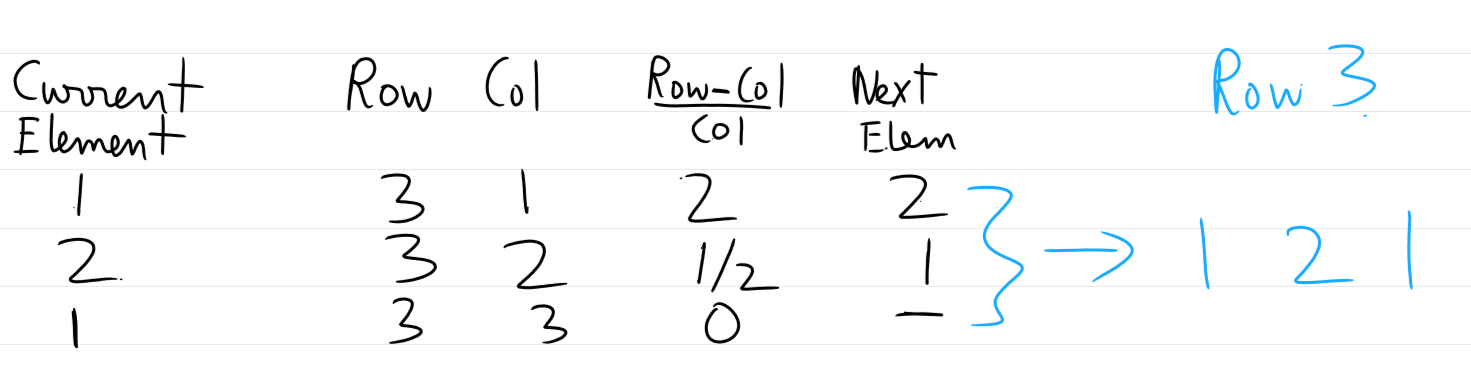
Row 4 :

& so on ...
How does this formula come into play ?? (More on that later...)
Algorithm
Run the outer loop to print each row.
Print leading spaces.
Print each element & calculate the next element using the formula.
Step 1: Running the outer loop
int n = 5; // user input
for (int row=1; row<n ; row++){
// new line for new row
printf("\n");
}
Step 2 : Printing the leading spaces

The red dots in the above image are leading spaces. These spaces give the triangle more of symmetric look.
int n = 5; // user input
for (int row=1; row<n ; row++){
for (int spaces = 1; spaces <= n-row; spaces++){
printf(" ");
}
// new line for new row
printf("\n");
}
To print spaces we use an inner loop that runs till n - row times.
Why n - row times?
So let's understand that through an example : So, let's say we are currently printing elements of row 2 and the n is 5 so n - row will be 3 , so that means there will be three spaces so that we can print two characters for row 2.
Step 3 : Print each element & calculate the next element using the formula
int n = 5; // user input
for (int row=1; row<n ; row++){
for (int spaces = 1; spaces <= n-row; spaces++){
printf(" ");
}
int elem=1;
for (int col=1;col<=row;col++){
printf("%4d",elem);
elem=elem*(row-col)/col;
}
// new line for new row
printf("\n");
}
So what happens is the first element of every row is 1. Then I run the inner loop for each column and the column number will be less than or equal to the row number so for example if the row is 2 then there will be only two columns, for row 3 there will be three columns like that .
For each column we will be printing an element, and the first element will be 1 and then the next element will be calculated by multiplying the current element with our formula.
Why do we need Pascal's triangle?
Pascal triangle is used in various places such as finding the coefficients in a binomial expansion, used in probability and in various other mathematical fields, so it is very necessary.
Binomial Coefficients
Binomial coefficients are coefficients in binomial theorem. Binomial theorem is a method to distribute powers (exponents) of binomials as shown below:
$$(a+b)^n=(^nC_0)a^nb^0+(^nC_1)a^{n-1}b^1+(^nC_2)a^{n-2}b^2+...+(^nC_{n})a^{0}b^{n}$$
Here coefficients are calculated using combinations. Combinations are a way of selecting a certain number of items from a collection where the order of selection does not matter. The formula for combinations is given by:
$$^nC_k=\frac{k!}{(n−k)!n!}$$
This is the formula we use to get coefficients of a binomial theorem.
Example : Using the binomial coefficient formula, we can get this below:
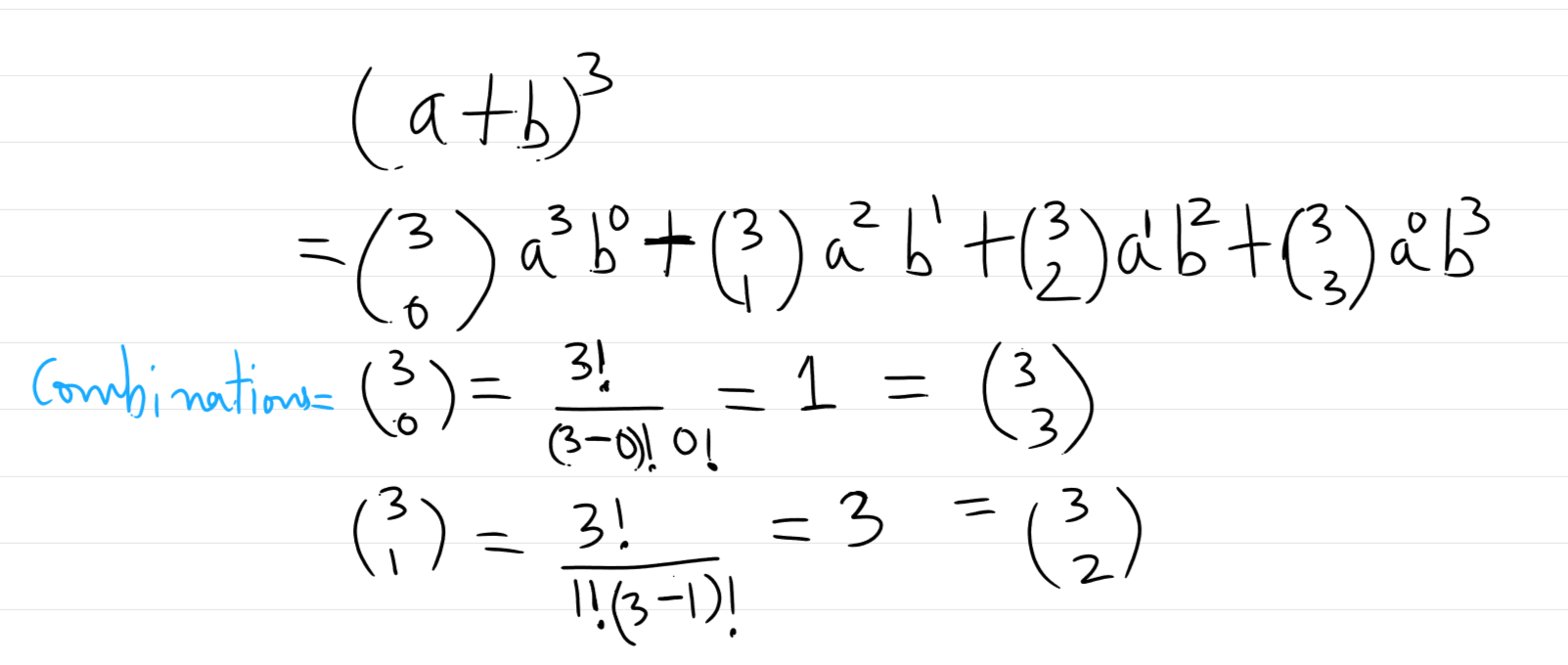
$$(a+b)^3=a^3b^0+3a^2b^1+3a^1b^2+b^3$$
So, taking the above equation as an example: we can say n = 3 ((a+b) to the power n)) then coefficients of each binomial respectively is 1, 3, 3, 1. Now see the row 3 of pascals triangle you will see 1331.
How does the simple formula we use comes in?
So the formula for finding coefficient is combination's formula where n = row number & k = column number. The combination formula C(n, k) involves factorials (n!& k!), which can quickly become very large for even moderate values of n. So it is very resource hungry.
Now there is a better formula which directly mirrors the recursive relationship between numbers in Pascal's Triangle that is : each number is the sum of the two above it.
So The binomial coefficient formula to get that recursive relationship is
$$C_{(r,c)}=C_{(r-1,c-1)}+C_{(r-1,c)}$$
Here r & c are rows & columns. Now you can derive our small formula consisting of rows & columns from this formula
Full Derivation :
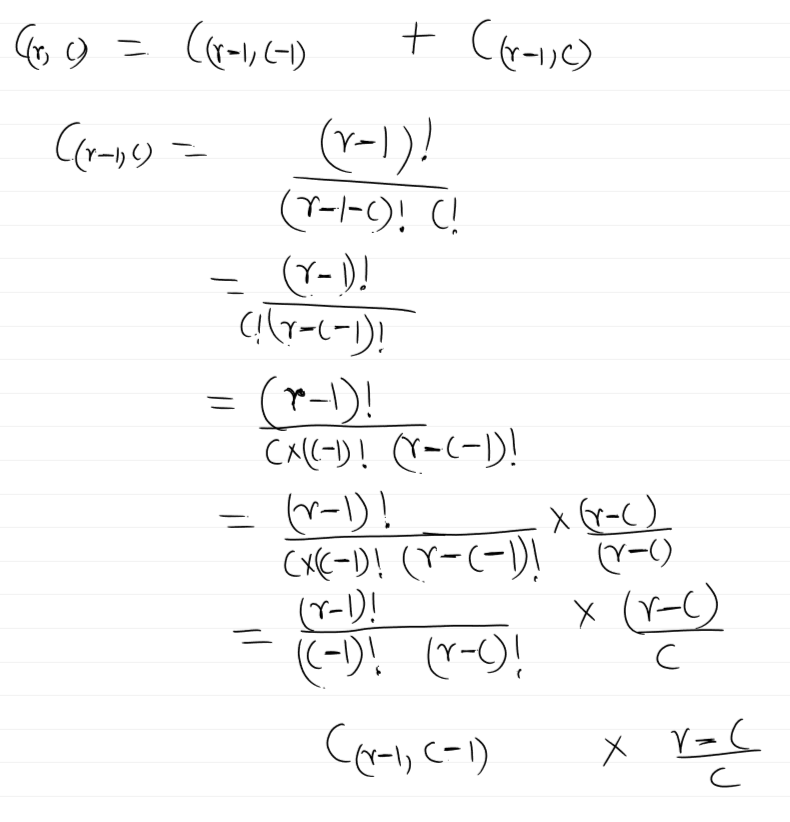
This means it is a recursive formula to get the next element in each row with row number & col number. Since we define the 1st element as 1, so calculating the next elements gets very easy.
Hope this helps 🚀
Subscribe to my newsletter
Read articles from Abhik Bhattacharya directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
