Introduction

This article offers an insightful exploration into the inner workings of the Hash join algorithm, explain it's two types one-phass and two-phase hash join, understanding its components in query plans. It delves into a detailed cost analysis and examines When the optimizer will preferred it over nested loop join

Hash Join Algorithm: Overview

The Hash Join algorithm is used to join two tables based on a specific condition, known as the join condition. It is particularly well-suited for equi-joins, which are joins where the condition is based on equality (e.g., table1.columnX = table2.columnY).. it has two main steps: the build and probe phases. Initially, the algorithm selects the smaller table to create a hash table, Subsequently, it iterates over the second table, using the hash function to identify and combine matching entries from the hash table based on the join condition.

Algorithm explanation

Assume Table R with M pages and m tuples, and Table S with N pages and n tuples
The Hash Join algorithm involves two main phases: the build phase and the probe phase. Below is the pseudo-code representation of these phases:

build hash table HTR for R
foreach tuple s ∈ S
output, if h1(s) ∈ HTR

Build Phase:
- Action: The algorithm starts by building a hash table HTR for the build table, which is typically the smaller of the two tables involved in the join. In our example, this is table R.
- Process: It hashes each tuple from the build table (table R) and stores it in HTR. The hash function used (h1) maps each tuple to a corresponding hash bucket in HTR.
Probe Phase:
- Action: Next, the algorithm iterates over each tuple s in the probe table (table S).
- Hash Check: For each tuple s, it computes the hash value using the same hash function (h1) and checks if this hash value exists in the hash table HTR.
- Output: If a matching hash entry is found (indicating a potential join match), the algorithm then verifies the join condition. If the condition is satisfied, the combined tuple from tables R and S is emitted to the result set.

One-Pass Hash Joins

Overview

One-Pass Hash Joins are used when the hash table for the smaller table (build table) fits entirely into the available memory. This approach is highly efficient as it minimizes disk I/O operations.

PostgreSQL Query Example

Tables: departments (2,000 rows) and employees (1,000 rows)
Query: Join departments and employees on department_id.

EXPLAIN ANALYZE SELECT d.department_id, e.name
FROM departments d
JOIN employees e ON d.department_id = e.department_id;

Hash Join // Probe Phase (Joining Data)
  (cost=25.00..100.00 rows=1000 width=150) (actual time=0.026..5.000 rows=1000 loops=1)
  Hash Condition: d.department_id = e.department_id
  -> Seq Scan on departments d  // Probe Phase (Outer Table Scan)
     (cost=0.00..10.00 rows=2000 width=50) (actual rows=2000 loops=1)
  -> Hash  // Build Phase (Hash Table Creation)
     (cost=10.00..10.00 rows=500 width=50) (actual rows=500 loops=1)
     Buckets: 1024  Batches: 1  Memory Usage: 64kB
     -> Seq Scan on employees e  // Build Phase  (Inner Table scan)
        (cost=0.00..20.00 rows=1000 width=100) (actual rows=1000 loops=1)

Lets Divide the Query Plan to 2 Parts
Part 1 : Build Phase Part

  -> Hash  // Build Phase (Hash Table Creation)
     (cost=10.00..10.00 rows=500 width=50) (actual rows=500 loops=1)
     Buckets: 1024  Batches: 1  Memory Usage: 64kB
     -> Seq Scan on employees e  // Build Phase  (Inner Table scan)
        (cost=0.00..20.00 rows=1000 width=100) (actual rows=1000 loops=1)

Seq Scan on employees e Node (Inner Table scan):
- Role in Build Phase: Initiates the Build phase. This step involves scanning the entire employees table ('e') to gather data for hash table construction.
- Node Detail: Seq Scan on employees e (cost=0.00..20.00 rows=1000 width=100) (actual rows=1000 loops=1)
  - Total Rows Processed: The scan processes 1000 rows, indicating it examines the full dataset of the employees table.
  - Width of Rows: Average row width of 100 bytes, suggesting the data volume handled per row.
  - Cost Estimate: A cost estimate from 0.00 to 20.00 shows the resource allocation for scanning each row and the preparation involved before the hash operation.
Hash Node (Hash Table Creation):
- Role in Build Phase:, this step constructs the hash table using the data from the inner set employees.
  - Hashing Each Row: In this pivotal phase, the database processes each row from the inner table, For every row, a specific hash function is applied to the join key - 'department_id'. This hash function is designed to convert the department_id into a unique hash value.
  - Bucket Insertion: Once the hash value is computed, the row is placed into a corresponding bucket in the hash table based on the computed hash value.
  - Creation of Hash Table: After processing all rows from the inner table employees, the hash table is fully constructed. This hash table represents an indexed version of the original table, organized based on the hash values of the join key.
- Node Detail: Hash (cost=10.00..10.00 rows=500 width=50) (actual rows=500 loops=1) Buckets: 1024 Batches: 1 Memory Usage: 64kB
  - Buckets: 1024 : Buckets in a hash table are like individual containers that store rows based on their hash value. The number 1024 indicates that the hash table has 1024 such containers.
  - Memory Usage: 64kB: This indicates the total amount of memory that the hash table uses.
  - Batches: 1
    - Single Batch Processing: The '1' batch in a hash join indicates that the entire hash table is processed in one pass.The single batch processing implies that the hash table, fits within the available memory.
    - Avoiding Disk-Based Operations in one phase join : Because the hash table is entirely resident in memory, there is no need to read or write data to/from disk during the hash join operation. This eliminates the slower disk-based input/output (I/O) operations that can introduce latency and performance bottlenecks.

Part 2 : Probe Phase Part

Hash Join // Probe Phase (Joining Data)
  (cost=25.00..100.00 rows=1000 width=150) (actual time=0.026..5.000 rows=1000 loops=1)
  Hash Condition: d.department_id = e.department_id
  -> Seq Scan on departments d  // Probe Phase (Outer Table Scan)
     (cost=0.00..10.00 rows=2000 width=50) (actual rows=2000 loops=1)

Seq Scan on departments d Node (Outer Table Scan):
- Role in Probe Phase:
  - Probing the Hash Table: After the hash table is built using the employees table in the Build Phase, the departments table enters the scene in the Probe Phase. Here, each row from the departments table is used to probe the hash table.
  - Sequential Scan: This step involves a sequential scan (Seq Scan) of the departments table, where each row is read one after the other.
- Node Detail: Seq Scan on departments d (cost=0.00..10.00 rows=2000 width=50) (actual rows=2000 loops=1)
Hash Join Node (Joining Data):
- Role in Probe Phase:
  - Executing the Join: This is where the actual joining of the departments and employees tables happens. The join condition (d.department_id = e.department_id) guides this process.
  - Utilizing the Hash Table: As each department_id from the departments table is read, the hash join algorithm quickly locates the corresponding bucket in the hash table created from the employees table.
  - Finding Matches: If the bucket exists it then checks each entry in that bucket to see if there’s an exact match. When it finds a match, it combines the data from both tables to form a joined row.

Efficiency in a One-Phase Hash Join

In-Memory Processing:
- Entire Operation in RAM: The key feature of a one-phase hash join is that the entire hash table, created from one of the tables (e.g., employees), fits into the system's memory (RAM).
- Immediate Access: Since all data resides in RAM, the database can access and process it much faster compared to disk-based operations.
Elimination of Disk I/O:
- No Disk-Based Operations: The one-phase approach avoids any disk I/O, which is beneficial because disk operations are significantly slower due to mechanical movements and higher latency.
- Continuous Processing: Since there's no need to temporarily store data on disk (as in multi-batch processing), the hash join proceeds continuously without interruptions for disk read/write operations.

One-Pass Hash Joins Algorithm cost analysis

The cost formula of one-pass join is R + S reflects the detailed steps of this process:
Reading the Build Table (employees):
- Sequential scan Cost (R): This cost involves reading inner table table employees from disk into memory. this I/O operation involves accessing all pages of the build table which will be R Pages.
Reading the Probe Table (departments):
- Sequential Scan Cost (S): This cost involves sequentially scanning the probe table (e.g., departments). Similar to the build table, this I/O operation involves accessing all pages of the probe table which will be R Pages
I/O Cost Emphasis: In the context of One-Pass Hash Joins, the formula for cost analysis gives priority to the I/O costs, which are often the most significant factor in the overall performance of the join process. ignoring the costs associated with building the hash table, hashing values, and the actual matching operations which are relatively faster since they occur in memory

Two-Pass Hash Joins

Overview

Two-Pass Hash Joins are employed when the hash table for the smaller table (build table) cannot fit entirely into the available memory. This approach involves two phases: partitioning and probing,

How it works

Estimation and Batch Processing:

Initially, the database planner estimates the memory needed for a hash table in a join operation. When it's determined that the hash table is too large for the allocated memory, the planner decides to process the data in batches by Partitioning of Inner and Outer Tables into batches so that each batch is fit in memory and process each batch separately

Partitioning of Inner and Outer Tables

Determining Partition Size : The first step is to determine how many partitions are needed. This is usually based on the amount of available memory and the size of the datasets. The goal is to ensure each partition is small enough to fit into memory during the join phase.
Selecting a Hash Function : hash function is selected that will distribute the data across partitions as evenly as possible. The function is applied to the join key
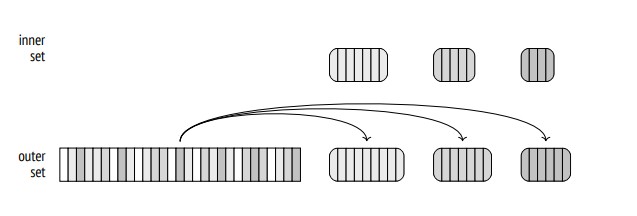
Creating Partitions for inner set: When a row from the reading the inner table is from disk, the hash function is applied to its join key to assign it to a partition. The row is then written to a temporary file specifically for that partition. this process happen until all the data is partitioned below (Figure 1) example of partition the inner set to 3 batches
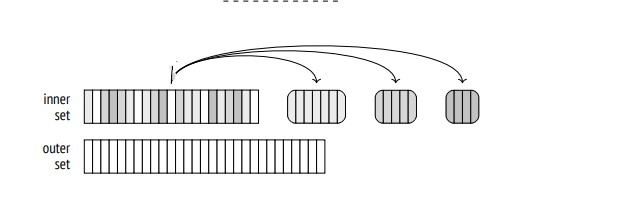
Creating Partitions for outer set: the same hash function is used to partition the outer set. below example (Figure 2) of partition the outer set to 3 batches
Writing To Disk : Each partition is stored in a separate temporary file on the disk. There is a set of partition files for the inner table and another set for the outer table.

Hash Table Creation and Probing Phase

Once the partitioning stage is complete, the join operation proceeds as described previously, with each partition loaded into memory one at a time:

Building In-Memory Hash Tables: For each inner partition loaded into memory, a hash table is built for it.
Probing with Outer Partitions: Then, the corresponding partition from the outer table is loaded. Each row from this partition is probed against the hash table of the inner table partition to find matching join keys.
Outputting Results: Matching rows are outputted as the result of the join operation for that partition.
Hash Table Creation and Probing Phase for Batches in Figures 1 and 2:
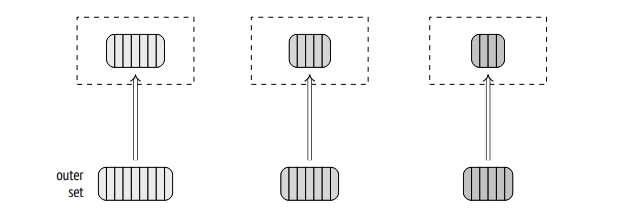
- First Batch Processing:
  - The first batch from the inner set is loaded into memory, and a hash table is constructed from its contents.
  - Next, the corresponding batch of the outer set is loaded into memory and probed against the hash table of the inner set.
  - Matching join tuples (rows) are written to a temporary results and save it to disk
- Repetition for Subsequent Batches :
  - The entire process, from loading an inner batch, creating a hash table, loading the corresponding outer batch, probing, and writing matching rows to disk, is repeated for each second and third batches from both the inner and outer sets.
Key Benefit of Partitioning in Two-Pass Hash Joins
- Use of Hash Function: The key to this partitioning strategy is the use of a hash function. This function is designed to distribute data across partitions in a way that each row is assigned to one and only one partition. The function is applied to the join key, which is a specific attribute used to match rows between tables.
- Consistent Partitioning Across Tables (The Critical point in Two-Pass Hash Joins): It's important to note that the same hash function is used for both inner and outer tables. This consistency ensures that any two rows from these tables that are supposed to match according to the join condition will end up in the corresponding partitions. Therefore, when a partition from the inner table is loaded into memory and joined with a partition from the outer table, there's no possibility of missing or mismatched rows due to them being in different partitions
- Avoiding Cross-Batch Complications: Without such a partitioning approach, there could be scenarios where related rows might end up in different batches, leading to incorrect or incomplete join results. The partitioning ensures that all potential matches for a given set of rows are contained within the same batch, thus maintaining the integrity of the join process.
- Complete In-Memory Loading: By partitioning the data sets, we ensure that each partition is small enough to be fully loaded into memory. This is crucial for performance, as it allows for faster access and processing of the data during the join operation without the need for extra Input/Output (I/O) operations..

PostgreSQL Query Example

Tables: tickets (300000 rows) and bookings (100000 rows)
Query: Join tickets and bookings on book_ref.

EXPLAIN ANALYZE SELECT t.ticket_no, b.book_ref
FROM tickets t
JOIN bookings b ON t.book_ref = b.book_ref;

Hash Join  (cost=100000.00..500000.00 rows=30000000 width=200) (actual time=500.000..10000.000 rows=30000000 loops=1)
Hash Cond: (t.book_ref = b.book_ref)
Buffers: shared hit=100000 read=500000, temp read=400000 written=400000
-> Seq Scan on tickets t  (cost=0.00..150000.00 rows=15000000 width=100) (actual rows=15000000 loops=1)
   Buffers: shared read=300000

-> Hash  (cost=50000.00..50000.00 rows=15000000 width=100) (actual rows=15000000 loops=1)
   Buckets: 131072 Batches: 128 Memory Usage: 32000kB
   Buffers: shared hit=100000 read=200000, temp written=250000
   -> Seq Scan on bookings b  (cost=0.00..50000.00 rows=15000000 width=100) (actual rows=15000000 loops=1)
      Buffers: shared hit=100000 read=200000

Lets Divide the Query Plan to Two Parts

Part 1 : Reading and Partitioning the Inner Table (bookings) into Batches

 -> Hash  (cost=50000.00..50000.00 rows=15000000 width=100) (actual rows=15000000 loops=1)
   Buckets: 131072 Batches: 128 Memory Usage: 32000kB
   Buffers: shared hit=100000 read=200000, temp written=250000
   -> Seq Scan on bookings b  (cost=0.00..50000.00 rows=15000000 width=100) (actual rows=15000000 loops=1)
      Buffers: shared hit=100000 read=200000

Seq Scan on bookings b Node (Inner Table scan):
- Role : This step involves scanning the entire bookings table ('b') to gather data for doing partition .
- Node Detail: Seq Scan on bookings b (cost=0.00..50000.00 rows=15000000 width=100) (actual rows=15000000 loops=1 Buffers: shared hit=100000 read=200000
  - Total Reads: read=200000 indicate the database reads 200,000 data blocks from the bookings table.
  - Shared Buffer Hits: shared hit=100000 indicate Out of these, 100,000 blocks are already in the shared buffer. The shared buffer is a memory space used by PostgreSQL to cache data blocks. A hit indicates that the data was found in the cache, reducing the need for disk access.
  - Disk Reads: The remaining 100,000 blocks are read from the disk, as they were not found in the shared buffer.
Hash Node ( Partition inner table bookings into batches)
- Role : This step involves partition the scanning rows in Seq Scan on bookings b Node into partition
- Partitioning into Batches : Due to the large size of the dataset (150,000,000 rows), the data is partitioned into batches for processing. This is because the entire dataset cannot fit into the available memory for the hash operation.
- Batches Count: The data is divided into 128 batches (Batches: 128). The choice of the number of batches is based on the size of the dataset and the available memory.
- Batch Processing: Each batch contains a portion of the bookings table data. PostgreSQL will process these batches one by one in the subsequent steps.
- Memory Allocation: Each batch will be processed later within the allocated 32,000 kB of memory (Memory Usage: 32000kB).
- Temp written=250000: refers to the total number of data blocks written to temporary disk space for all inner created batches
- Read=200000: This shows the number of data blocks read from the disk into the shared buffer to read the inner table.
- Shared hit=100000: This metric indicates the number of times data requested was found already in the shared buffer (cache), thus avoiding the need to read it from disk
- Buckets Allocation:
  - The mention of Buckets: 131072 buckets in the plan is an indication of how PostgreSQL intends to structure the hash table. However, it doesn't mean the hash table has been created yet.
  - At this stage, PostgreSQL is essentially preparing for the hash operation by deciding on the number of buckets that will be needed.
  - The actual creation and population of the hash table with data occur later, during the processing of each batch.

Part 2 :

Reading and Partitioning the Outer Table (tickets) into Batches
Processing inner and outer batches

      Hash Join  (cost=100000.00..500000.00 rows=30000000 width=200) (actual time=500.000..10000.000 rows=30000000 loops=1)
      Hash Cond: (t.book_ref = b.book_ref)
      Buffers: shared hit=100000 read=500000, temp read=400000 written=400000
      -> Seq Scan on tickets t  (cost=0.00..150000.00 rows=15000000 width=100) (actual rows=15000000 loops=1)
         Buffers: shared read=300000

Seq Scan on bookings b Node (Inner Table scan): :
- Role : This step involves scanning the entire tickets table ('t') to gather data for doing partition .
Hash Join Node
- Role: This step involves
  1. Partitioning Rows from tickets Table: The rows retrieved from the Seq Scan on the tickets table (outer table) are partitioned into batches.
  2. Reading inner batch and Building Hash Table: After partitioning the data for the tickets table in step 1, PostgreSQL starts processing inner batches. For each batch of the bookings table is loaded in memory, a hash table is created for it.
  3. Reading outer batch and doing Probing: For each inner batch, a hash table is created in step 2, the corresponding outer batch (from the tickets table) is read into memory, and a probing operation is performed. This involves matching the rows from the outer batch against the hash table created from the inner batch.
  4. Process Iteration: step 2,3 — loading the inner batch, hash table building, reading corresponding outer batch , and probing — is repeated for all batches.
- Node details
  - read=300000 This metric shows the total number of data blocks read from disk into memory for the entire hash join process, It includes reads for both the tickets and bookings tables.
  - hit=100000 : This indicates the number of times data requested for the hash join operation was found in the shared buffer and did not require reading from the disk. It represents cache hits for both tickets and bookings table data for the entire hash join process.
  - temp written=400000 : This indicates the total number of blocks written to temporary disk storage during partitioning the tickets table and bookings table
  - Temp read=400000 his refers to the number of blocks read from temporary storage on disk. It likely encompasses reading the partitioned data (batches) of both the tickets and bookings tables

Two-Pass Hash Joins Algorithm cost analysis

Total I/O Cost: The total cost, 3(M + N), reflects the combined I/O operations of reading and writing both tables in its partitioning and probing phases. The process involves reading and writing both tables to disk for partitioning (2(M + N) I/Os) and an additional read during probing (M + N I/Os)

Partitioning Phase:Process:

Read Operation: Each block from both tables is read from disk. This is necessary to process and partition the data.
Write Operation: After reading, the data is partitioned based on a hash function, and these partitions (or batches) are written back to disk
Cost Analysis:
- I/O Cost for Partitioning: 2(M + N)
  - This cost comes from reading (M + N) and then writing (M + N) the partitions of both tables to disk.

Probing Phase:

Purpose: In this phase, the partitions are loaded back into memory, in pairs, to perform the actual join operation.
Process:
- Read Operation: Each partition (batch) of one table is read into memory and joined with the corresponding partition of the other table.
- This process is repeated for each pair of partitions until all partitions have been processed.
Cost Analysis:
- I/O Cost for Probing: M + N
  - Every block from both partitions (M and N) is read again from disk during this phase to doing the prob.

When the Optimizer Prefers Hash Joins

Notice : Article 1: Nested Loop Join is prerequisites to understand this section

Hash Join Efficiency Based on Selectivity:

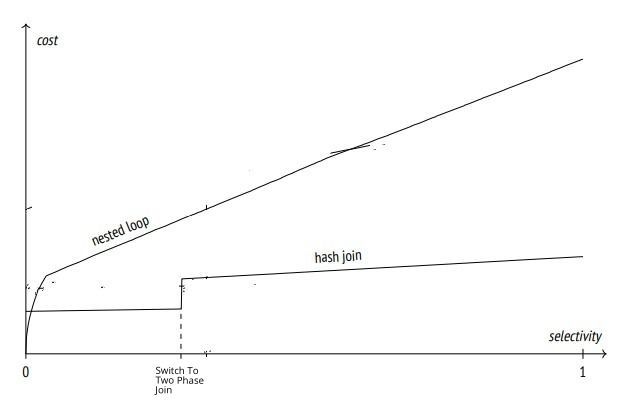
Low Selectivity (low or Moderate Rows Matches):

Nested Loop Join :
- Operation: At low selectivity, the nested loop join operates efficiently when there is an index on the join key of the inner table and low or moderate rows found. It can quickly locate matching rows by leveraging the index, avoiding a full table scan.
- Performance: It's highly performant For Low selectivity where an index prevents scanning the entire inner table, thereby reducing disk I/O.
- Optimizer Choice: The optimizer prefers this join method when it predicts that the number of qualifying rows will be minimal because it can avoid the seq scan for the inner table to build the hash table in hash join algorithm.
Hash Join:
- Overhead: At this level of selectivity, the upfront cost of creating a hash table for the hash join is not justified if only a few rows from the inner table will match.
- When Preferred: However, if no index is available for the nested loop join, the optimizer may still choose a hash join, as a full scan required by the nested loop join would be more expensive for every lookup.

Medium Selectivity:

Nested Loop Join :
- Performance Dynamics:
  - At medium selectivity, a nested loop join with an index on the inner table remains efficient but begins to face challenges. Although the index helps in quickly locating matching rows, the increased number of matches means more index lookups are required.
  - The cost efficiency of the nested loop join now depends heavily on the effectiveness of the index and the distribution of data. If the index leads to fast retrieval of the matched rows, the nested loop join can still be a good choice otherwise hash join will be preferred .
Hash Join:
- Efficiency in Lookup for increasing of number of matches :
  - For medium selectivity, the hash join becomes more competitive, especially in cases where the nested loop join's index is less effective. The initial cost of building the hash table is balanced by the efficient lookup for a larger number of matches.
    - Initial Cost vs. Lookup Efficiency: The initial cost of building the hash table can be high, but once it's built, finding matches for a larger number of records is much faster because it's in memory operations compared to the repetitive comparisons in a nested loop join and overhead of I/O's.
    - Balance of Costs: The hash join's initial cost is balanced by its more efficient handling of a larger number of matches, which is a common scenario in medium selectivity.
  - This linear cost growth is a significant advantage for hash joins as it scales well with increasing data volume and larger number of matches.

High Selectivity:

Nested Loop Join:
- Index Scan Intensification: At high selectivity, the nested loop join faces significant challenges due to the sheer volume of rows that match the join condition. This situation leads to a dramatic increase in the number of index scans as it tries to locate each matching row in the inner table.
- Performance Impact: The increase in index scans can drastically impact performance, as each scan adds to the total execution time. The nested loop join, which was efficient at lower selectivities, becomes less optimal due to this repetitive process.
- Comparative Inefficiency: In scenarios of high selectivity, the overall time taken for numerous index scans in a nested loop join can potentially exceed the time it would take to perform a sequential scans in hash join method.
Hash Join:
- Handling High Selectivity: The hash join method tends to handle high selectivity more gracefully. Once the hash table is built from the inner table, it can quickly match a large number of rows from the outer table against this hash table.
- Efficiency in Bulk Matching: The efficiency of hash joins comes from their ability to handle bulk matching operations effectively, which becomes a significant advantage at high selectivity levels.
- Balancing Initial Cost and Execution Time: Although the initial cost of creating a hash table can be substantial, this cost is often offset by the faster matching process, especially when dealing with a high volume of matches. The hash join avoids the repetitive index scans of nested loop joins and overhead of I/Os, leading to overall better performance in high selectivity scenarios
Peak at "Switch To Two Phase Join": The peak labeled "Two Phase Join Chosen" on the graph signifies a tipping point in the cost of hash joins. At this juncture, the dataset is too large to be accommodated in the available memory making switch to two phase join, This method incurs higher costs due to increased disk input/output operations here is detailed explanation .
- Memory Constraint: The peak indicates a point where the hash join algorithm needs to switch to a more complex strategy, such as a two-phase join, because the hash table no longer fits in memory
- Partitioning Overhead: This change is due to the necessity to partition the dataset and process it in parts. The hash join initially builds a hash table in memory for quick access, but when the data set is too large, it must be divided into smaller parts that can be individually processed (partitioned).
- Cost Implications: This method is more costly than a simple in-memory hash join because it requires additional steps: partitioning the data, writing the partitions to disk, reading them back into memory for processing, and then merging the results. These steps significantly increases the input/output (I/O) operations.
High Selectivity Query Example :
- Refer back to the High Selectivity Query Example Leading the Optimizer to Switch to Hash Join Example in previous article in this section Optimizer Prefers Nested Loop Joins section Loop

Summary

The Hash Join algorithm, operates through two key phases: the build phase, where it creates a hash table from the smaller table, and the probe phase, for matching entries in the larger table, proving especially effective in equi-join scenarios. Its efficiency varies with dataset size; the One-Pass Hash Join, applied to smaller datasets that fit in memory, minimizes disk I/O operations, captured in the cost formula R + S. For larger datasets, the Two-Pass Hash Join takes over, necessitating data partitioning and incurring higher I/O costs, reflected in the formula 3(M + N). Selectivity also plays a crucial role, with low selectivity favoring Nested Loop Joins for their minimal I/O, while medium to high selectivity tilts the balance towards Hash Joins due to their efficient bulk matching capabilities, even considering the initial overhead of creating a hash table

Query Execution Part 2: Join Algorithms - Hash Join

Table of contents