Petri Nets for Web3 Decentralized Applications

Petri nets are state machines and mathematical models which can be used to describe and analyze concurrent processes and state transitions within those processes. They are named after their inventor, Carl Petri, who created them in 1939 (when he was 13!) to define chemical processes, and two decades later were the basis of his PhD dissertation.

Petri Nets consist of places, transitions, arcs, and tokens. Places (or nodes) represent states (or conditions), transitions depict events (or actions), and arcs define flow of tokens between places and transitions. Petri Nets have been used as a framework for modeling and simulating systems such as manufacturing processes, communication protocols, and have now been found to be useful in recent decentralised software architectures.

There are hundreds of research papers specifically on Petri nets and many thousands of citations of Petri nets. The theoretical discussions can be extremely deep, but this article will not go there! Feel free to explore on your own, I am sure you will find something that will pique your interest.

This article is a casual dive into the use of a Petri net as a design pattern for two basic smart contracts, with actual runnable code for the Internet Computer (ICP). Note: this code is for demo purposes and basic proof-of-concept goals. Full production-ready code would certainly demand more work for rigour and completeness.

Petri Nets vs. Finite State Machines

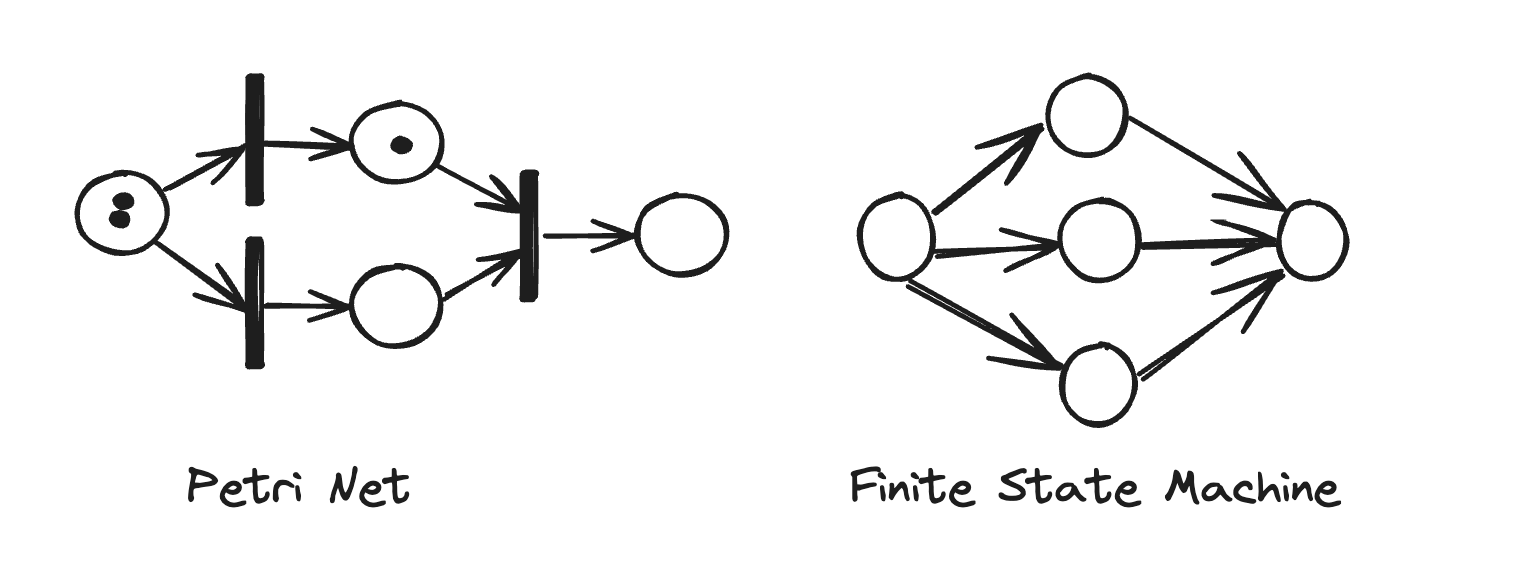
A Petri net is a state machine which can model concurrent systems. Concurrent systems are difficult to model with a finite state machine, as an FSM typically maintains a single current state. In a typical FSM, the state changes after a single event, while in a Petri net, multiple transitions may be executed if conditions are met based on tokens.

This simple diagram has two nodes in the middle of a Petri net representing parallel intermediate states based on the number of tokens in the node. The vertical bars are transition processes with input and output arcs. Contrast this with the finite state machine which requires at least more than two nodes to represent individual sequential intermediate states.

Rationale for Using Petri Nets in Internet Computer (ICP) Decentralized Applications (DApps):

There are advantages using Petri nets instead of simple state machines as a design pattern for smart contracts and distributed applications.

• Dynamic State Transitions: DApps can involve dynamic state changes triggered by multiple events or conditions. Petri Nets provide a more flexible framework for modeling this, supporting more sophisticated logic which often drive smart contracts.

• Formal Verification: DApp models using Petri Nets can be used with formal methods to verify liveness, deadlock-freedom, safety, and ensuring the integrity of the decentralized environment.

• Scalability and Modularity: Petri Nets enforce modular design principles and decomposition of complex DApps into smaller, manageable components. This enhances scalability and maintainability.

• Visualization and Documentation: Petri Nets provide a better visual and intuitive representation of DApp logic, and a means of collaboration and communication between developers and product designers.

• Decentralized Governance and Interoperability: Petri Nets provide better modeling in support of decentralized governance and methods.

Cautionary Advice on Using Petri Nets
Here are some counter-arguments to the rationale for using Petri Nets as a design pattern:

• Complexity: Petri Nets can introduce complexity, and certainly a learning curve for those not familiar with Petri Nets.

• Limited Tooling and Support: The limited tools and packages supporting Petri Nets could hinder development and wide adoption, making it a challenge for developers to efficiently and correctly utilize Petri Nets.

• Overhead in Verification: Despite the existence of formal methods for Petri nets, the process and lack of tooling are limited and time consuming.

• Scalability Concerns: Despite Petri Nets modularity and scalability benefits in theory, in practice that might be another story. Complex interactions and dependencies between modules and contracts can become challenging as size and complexity increase.

• Alternative Modeling Approaches: Finite state machines offer simpler representations of smart contracts and may be more intuitive for developers to understand and work with, especially for smaller-scale contracts or more sequentially designed DApps.

Petri Net Example: Producer - Consumer Model

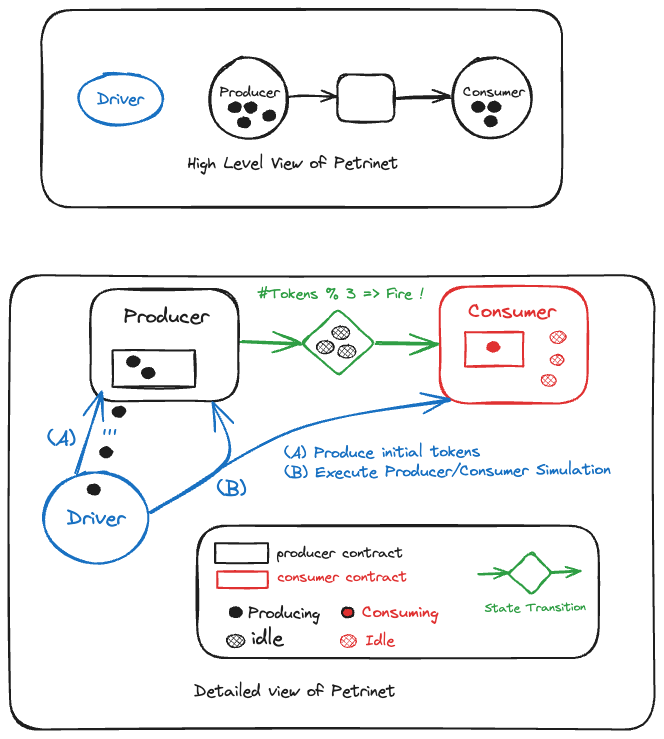
This example uses a Petri net to model a producer-consumer application. The high level view shows the producer and consumer nodes, with arcs between them showing the flow thru a transition process. The second diagram gives a little more details: a driver initializes idle tokens for production, the tokens are consumed based on production count, divisible by 3 in this case. Once consumed the tokens are then “deleted” in the idle state. The producer and consumer nodes implement their own "smart contract".

Implementation: Internet Computer (ICP) and Motoko

The example Petri net is implemented in Motoko as a single actor. The Petri Net consists of nodes, tokens, states, and transitions. Motoko uses asynchronous functions to model the behavior of a producer and a consumer, interacting with a shared state thru transition code.

The Motoko programming language is a new, modern and type safe language for developers who want to build the next generation of distributed applications to run on the Internet Computer blockchain network. For more see the Motoko Documentation in the references.

Elements of the Petri net:

The Petri net actor defines types for State Token Transition and Node. The transition functions are the contract code, two functions producerContract and consumerContract. The nodes are initialized with their token count and state.

    type State = { #Idle; #Producing; #Consuming };
    type Token = { count : Nat; state : State };
    type Transition = shared (Token) -> async Token;
    type Node = { token : Token; transition : Transition };

    var producerNode : Node = {
        token = { count = 0; state = #Producing };
        transition = producerContract;
    };

    var consumerNode : Node = {
        token = { count = 0; state = #Consuming };
        transition = consumerContract;
    };

A common function fireTransition calls the transition function, and each node has a driver to call the transition function which modifies the nodes tokens.

    // Transition execution function
    private func fireTransition(node : Node) : async Node {
        var mutableToken = await node.transition(node.token);
        return { node with token = mutableToken };
    };

    public func producer() : async Node {
        producerNode := await fireTransition(producerNode);
        consumerNode := { consumerNode with token = producerNode.token };
        return producerNode;
    };

    public func consumer() : async Node {
        consumerNode := await fireTransition(consumerNode);
        producerNode := { producerNode with token = consumerNode.token };
        return consumerNode;
    };

The contract code for the producer is simple, just increment the token count and set the state as idle, waiting to be consumed.

    public func producerContract(t : Token) : async Token {
        return {
            count = t.count + 1;
            state = #Idle;
        };
    };

The contract code for consumer is a little more complex. The consuming process occurs when a condition is true, in this case, if token count is divisible by 3. Then all tokens are processed while the state is Consuming. Work is simulated with a function doThingsAndUpdate and the updated token object is returned.

    public func consumerContract(t : Token) : async Token {
        var token = t;
        // start consuming when token count is multiple of 3
        if (token.count % 3 == 0) {
            token := {t with state = #Consuming};
        };
        // consume until consuming state is false or count = 0
        while (token.state == #Consuming and token.count > 0) {
            token := {
                count = token.count - 1;
                state = await doThingsAndUpdate(token);
            };
        };
        return token;
    };

The doThingsAndUpdate function uses randomness to update the token state to be consuming or idle. If a (large) random number is divisible by the token count then the state is returned to Idle, which will halt consuming, else the consuming state continues.

    private func doThingsAndUpdate(token : Token) : async State {
        let randomNumberOpt = await getRandom();
        switch (randomNumberOpt) {
            case (null) { return #Idle };
            case (?randomNumber) {
                if (randomNumber % token.count == 0) {
                    return #Idle;
                } else {
                    return #Consuming;
                };
            };
        };
    };

A driver method initializes the producer tokens, and runs the producer-consumer process until no tokens are left in the consumer node.

    public func driver(n : Nat) : async Nat {
        var loopCount : Nat = 0;
        for (i in Iter.range(0, n - 1)) {
            ignore await producer();
        };
        while (consumerNode.token.count > 0) {
            ignore await consumer();
            loopCount += 1;
            if (consumerNode.token.count > 0) {
                ignore await producer();
            };
        };
        return loopCount;
    };

On the Internet Computer the functions can be called directly thru the backend canister.

Here is an example to call a driver where producer tokens are initialized to 12:

% dfx canister call <backend-canister-id> driver '(12)'

I added a simple front end to call the driver method. The driver function returns the number of iterations required to consume all tokens. Here is a screen shot

The entire code base is in my repo, with instructions for deployment and other documentation. https://github.com/carlek/petrinet_producer_consumer

This is simple proof-of-concept code. Extensions to this would be a more complex token schema, where more attributes are within a token object to support a complex contract and state transition logic.

After this little exercise, a simple Producer-Consumer model, within a distributed application, I believe using a finite state machine would be cumbersome. The Petri net in my opinion, is a much better design pattern.

References

Motoko Language Reference

Research articles: Petri Nets