Loss functions are a way to quantify the performance of an algorithm. They are feedback mechanisms that demonstrate how well your algorithm has understood its learning dataset. If the value is high it is making a large loss which means that the algorithm is not able to capture majority data. Our goal is to minimize the loss function.

Loss functions in deep learning capture the mathematical relationship between the input parameters (weights and biases of the neural network) and the output results.

Loss Functions are not Cost Functions.

Loss functions are derived on the basis of a single data point, while a cost function is the aggregate of all the loss functions over the entire dataset. The cost function is what the optimization algorithm minimizes during the training process.

Regression Losses

Loss Function	Mean Squared Error (MSE)	Mean Absolute Error (MAE)	Huber Loss
Definition	average of squared difference between predictions and actual observations.	the average of sum of absolute differences between predictions and actual observations.	takes the advantageous characteristics of the MAE and MSE functions and combines them into a single loss function.
mathematically	MSE = (1/n) * Σ(yᵢ - ȳ)²	MAE = (1/n) * Σyᵢ - ȳ
Also known as	L2 loss	L1 loss	smooth absolute error
Use Case	Use Mean Squared Error when you desire to have large errors penalized more than smaller ones.	Suitable when the distribution of errors is expected to be asymmetric or when you want to focus on the magnitude of errors without emphasizing outliers.	The crucial parameter in the Huber loss is denoted as delta (δ), acting as a threshold that establishes the numerical limit for deciding whether the loss should be calculated using a quadratic or linear approach.
Advantage	Simple and commonly used	Robust to outliers	The hybrid nature of Huber Loss makes it less sensitive to outliers, just like MAE, but also penalizes minor errors within the data sample, similar to MSE.
Disadvantage	Sensitive to outliers	Optimization may be more challenging because the gradient is constant for all errors, making it less informative for the direction of parameter updates.	Requires tuning of the δ parameter

the MAE and MSE are errors that are efficiently explained in the table. Lets continue with understanding the Huber Loss is detail.

Huber Loss

The mathematical equation for Huber Loss is as follows:

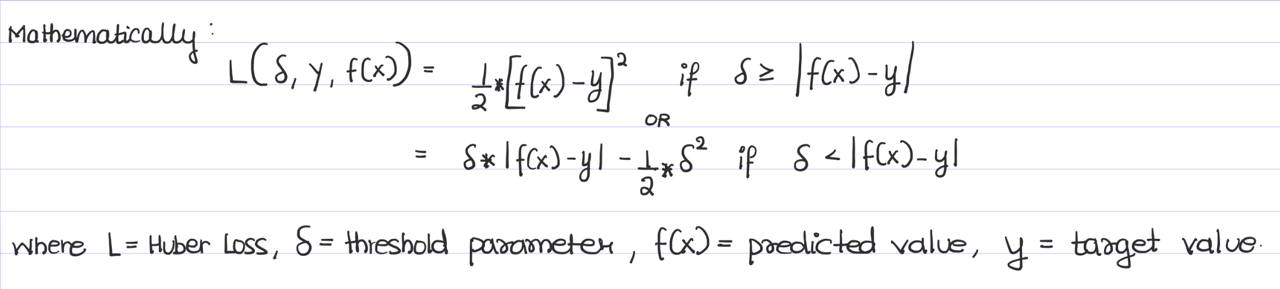
The Huber Loss has two modes depending on the delta parameter. The modes are linear or quadratic.

Quadratic Component for Small Errors (1/2) * (f(x) - y)^2 : characterizes the advantages of MSE that penalize outliers; within Huber Loss, this is applied to errors smaller than delta, which ensures a more accurate prediction from the model.

Linear Component for Large Errorsδ * |f(x) - y| - (1/2) * δ^2: utilizes the linear calculation of loss similar to MAE, where there is less sensitivity to the error size to ensure the trained model isn’t over-penalizing large errors, especially if the dataset contains outliers or unlikely-to-occur data samples.

If you like the blog so far make sure to like and share it!

Classification Losses

Loss Function	Binary Cross-Entropy Loss or Log Loss	Categorical Cross-Entropy Loss	Hinge Loss
Definition	measures how far off a machine learning model's predictions are from the actual target values. It does this by summing up the negative logarithm of the predicted probabilities.	This loss function uses the negative logarithm of the predicted probability assigned to the correct class for each sample and sums these values across all samples. It is an extension of Binary Cross-Entropy Loss to handle more than two classes.	quantifies the classification error of a machine learning model by measuring the distance between its predictions and the decision boundary.
Use Case	logistic regression problems and in training ANNs designed to predict the likelihood of a data sample belonging to a class and leverage the sigmoid activation function internally.	multiclass classifications	maximum margin classifications
Advantages	Standard choice for binary classification tasks	Common choice for multiclass classification	Effective for SVMs, encourages robust decision boundaries
Disadvantages	May struggle with class imbalances and noisy labels	Requires one-hot encoding of class labels	Not differentiable, which can limit certain optimization methods

References

https://www.datacamp.com/tutorial/loss-function-in-machine-learning

Conclusion

And there you have it! We have covered the fundamentals of loss functions completely. I hope this blog serves as a good place for quick reviews. Like share and comment!

Loss functions