Dijkstra’s Algorithm —
 Saurabh verma
Saurabh vermaIn this article we are going to understand one of the most popular distance finding algorithm with non-negative edge weights in Graph.
(Source: Wikipedia)
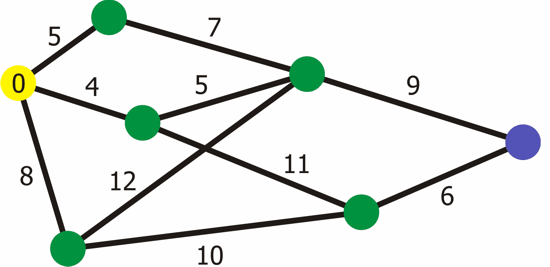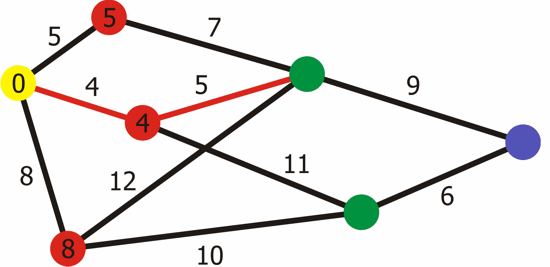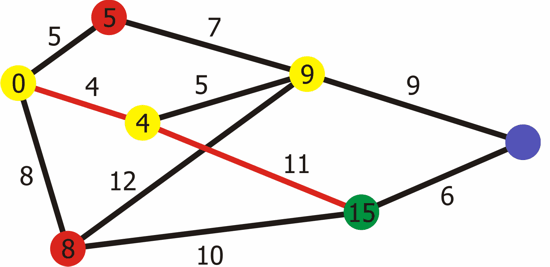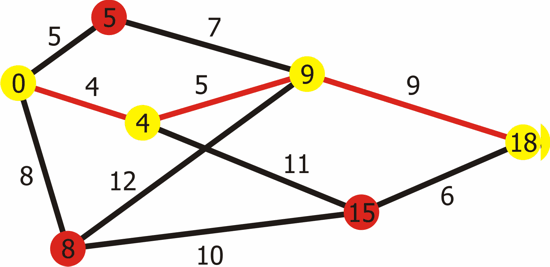
Problem Statement:
Given a weighted graph G with vertices V and edges E, and a source vertex s, the goal is to find the shortest paths from the source vertex s to all other vertices in the graph.
Algorithm Steps:
Initialization:
Initialize a distance array dist[] where dist[i] represents the distance from the source vertex to vertex i.
Set dist[s]=0 and dist[v]=∞ for all other vertices v.
Create a priority queue (or min-heap) to store vertices and their current distances. Enqueue the source vertex with distance 0.
Main Loop:
While the priority queue is not empty, do the following:
Dequeue the vertex u with the minimum distance from the priority queue.
For each neighboring vertex v of u, calculate the total distance from the source to v through u. If this distance is smaller than the current known distance to v, update dist[v] and enqueue v with the new distance.
Termination:
- Once the priority queue is empty, the algorithm terminates, and the dist[] array contains the shortest distances from the source to all other vertices.
V - Destination U - source
#include <bits/stdc++.h>
using namespace std;
// ∞
const int INF = numeric_limits<int>::max();
// You can put the any large value at the place of infinite such as
// Maximum value of Integer.
class Graph {
private:
int numNodes;
vector<vector<pair<int, int>>> adjacencyList;
public:
//constructor for the Graph class
Graph(int n) : numNodes(n), adjacencyList(n) {}
// Function to add an edge to the graph u- source v-destination
void addEdge(int source, int destination, int weight) {
// Uncomment for undirected graph
adjacencyList[source].push_back({destination, weight});
adjacencyList[destination].push_back({source, weight});
}
// Function to perform Dijkstra's algorithm
void dijkstra(int start) {
// Priority queue to store nodes and their distances
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
// Vector to store distances from the start node
vector<int> distance(numNodes, INF);
// Set the distance of the start node to 0
distance[start] = 0;
// Add the start node to the priority queue
pq.push({0, start});
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
for (const auto& edge : adjacencyList[u]) {
int v = edge.first;
int weight = edge.second;
// Relaxation step
if (distance[u] + weight < distance[v]) {
distance[v] = distance[u] + weight;
pq.push({distance[v], v});
}
}
}
// Print the distances from the start node
cout << "Shortest distances from node " << start << ":\n";
for (int i = 0; i < numNodes; ++i) {
cout << "To node " << i << ": " << (distance[i] == INF ? "INF" : to_string(distance[i])) << "\n";
}
}
};
int main() {
Graph graph(6);
// Adding edges to the graph U = 0,V = 1,W = 2(weight on a edge)..
graph.addEdge(0, 1, 2);
graph.addEdge(0, 2, 4);
graph.addEdge(1, 2, 1);
graph.addEdge(1, 3, 7);
graph.addEdge(2, 4, 3);
graph.addEdge(3, 4, 1);
graph.addEdge(3, 5, 5);
graph.addEdge(4, 5, 2);
// Starting node for Dijkstra's algorithm
int startNode = 0;
// Perform Dijkstra's algorithm using class and object
graph.dijkstra(startNode);
return 0;
}
Output
Shortest distances from node 0:
To node 0: 0
To node 1: 2
To node 2: 3
To node 3: 9
To node 4: 6
To node 5: 8
Dijkstra's algorithm is widely used in various applications
Airline Flight Path Planning:
- Airlines use Dijkstra's algorithm to determine the most cost-effective flight paths, taking into account factors such as fuel consumption, airspace restrictions, and flight times.
Routing Protocols in Computer Networks:
- Dijkstra's algorithm is often used in computer networking protocols like OSPF (Open Shortest Path First) and IS-IS (Intermediate System to Intermediate System) to find the shortest path between routers.
Traffic Engineering
Supply Chain Management
Time Complexity:
The time complexity of Dijkstra's algorithm depends on the data structures used for priority queue operations. With a simple array implementation or a binary heap, the time complexity is O((V+E)logV).
Thank you for reading my content. Be sure to follow and comment on what you want me to write about next 🤓
Subscribe to my newsletter
Read articles from Saurabh verma directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Saurabh verma
Saurabh verma
Hey, I am Saurabh Verma, an undergrad student learning Full stack Web Development. I will be focusing on Full stack Web development and DSA in my blogs.