MFKeyAttack: MIFARE Classic Protocols Analyzing && LFSR + CRYPTO1 Exploitations
 Patrick Peng
Patrick PengIt seem like this research team in Radboud University did a really impressive work! Firstly, they did analysis on the entire Mifare Classic System, which is one of the most dominate Contract-less system for cards used in modern society; After that, they found two vulnerabilties that this system contains. Which would leads to serious consequences; And now, lets dig in to them!
In the paper, the reseacher dig deep into how Mifare Classic Cards works. Which can be seperated into The logical structure and the Authentications.
Logical Structure of the MIFARE Classic Tags
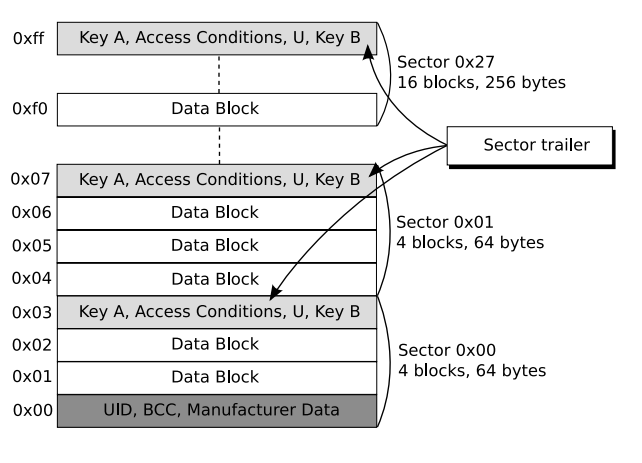
To actually know about the MFKey32 Attack, We must firstly know the basic structure of MIFARE Classic tag. Firstly, the memory unit in the MIFARE Classic tag is seperated into sector, and just similar to heap management of Glibc, each sector is divided into blocks of 16 bytes each. Additonally, the last block of each sector (sector trailer) stores two secret keys and access conditions to that sector. These two key for that sector is very essential since every every operation for that block must firstly go through the authentication for the sector (Including Read,Write,etc).
These keys are very essential also for clone or simulating MIFARE Classic cards, since we can't read or write these sector (which could store essential information), thus, cracking these keys would be of our main goal.
Authentications
For the authentication protocol of MIFARE Classics, it envolved complex mathmatical operations such as CRYPTO1 Cipher, Hitag2 Cipher and etc, thus, we will be focusing on the understanding these concept and how thet work
Protocols
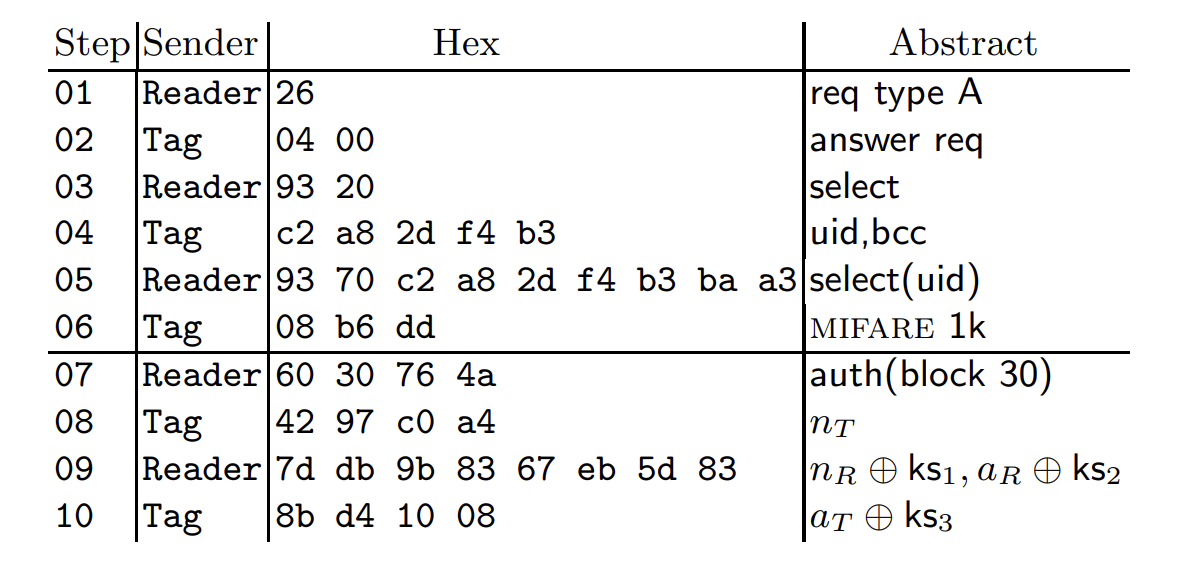
The basic concept that MIFARE Classics using is really easy understanding, Firstly, for authentications,the reader will sends authentication request for a specific block in each sector, as a response, the tags in MIFARE Classics will pick a challenge nonce (nT). Then the reader sends its own challenge nonce (nR) together with the answer (aR) to the challenge of the tag. The tag finishes authentication by replying (aT) to the challenge of the reader; Thus these are things generated per on communication:
nT: challenge nonce for MIFARE Classic tags
nR: challenge nonce for READER
aR: anwser for answer for the challenge of MIFARE Classic tags
aT : Finished code that MIFARE Classic tags sends.
To be notice, The pseudo-random generator in the tag used to generate nT is a 16 bit LFSR(which we will explain later) Since nonces are 32 bits long and the LFSR has a 16 bit state, the first half of nT determines the second half. Meaning that given a 32 bit value, we can tell if it is a proper tag nonce.
Linear Feedback Shift Register (LFSR)
&& CRYPTO1 Cipher
Understanding LFSR will be very important for our exploring trip, since that most parts of CRYPTO1 Cipher depends on this way of randoms-generation (More specifily, 48-bit linear feedback shift register)
Linear Feedback Shift Register (LFSR)
The theory behind LFSR is really not that hard to understand as it sounds like, basiclly, per every clock tick. the register will be firstly shifted left on bit, After that, the feedback bit will be used as a parameter for a function (linear) which generates a new input bit fed on the right. To be notice that, this specific generation method depends entirely on the inital states of this register. In which leads to another vulnerabilty that will be mention
CRYPTO1 Cipher's 48-bit LFSR
The Cipher for Mifare Classic Cards CRYPTO1 Also depends on LFSR as mentioned before, Nevertheless, CRYPTO1 uses a 48-bit version of LFSR, Even though 48-bit sound really long, however, 48 bit is considered weak in modern Cryptography, but that's not our main focus, as mentioned above, the flaw that LFSR depends solely on the inital states of register leads us to our other step: Is it possible to attack CRYPTO1 via caculation of the inital states? And the answer, is yes.
Exploiting Initialization
To exploit the initialization of CRYPTO1, we must know whats effecting the inital states of register of this 48-bit version LFSR, in the paper, the research team conducted deductions of factors that might influence the inital states of this 48-bit version LFSR.
As we mention in Section 4, if nT ⊕ uid remains constant, then the encrypted reader nonce also remains constant. This suggests that nT ⊕ uid is first fed into the LFSR
if special care is taken with the feedback bits, it is possible to modify nT ⊕uid and the secret key K in such a way that the ciphertext after authentication also remains constant.
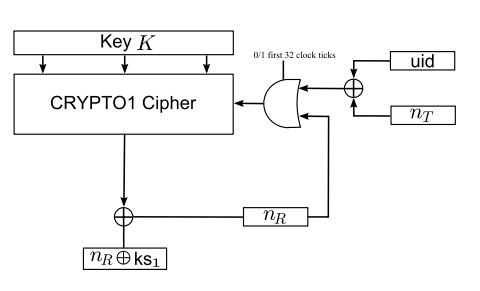
Thus, according to the deduction, it will be possible for us to gain total controll of the state of LFSR by choosing appropriate UID,K,nT*, before feeding in the reader nonce. However, in practise of real life situations, *Only by sending an appropriate 48 bit tag nonce nT , we can fully control the state of the LFSR just before the reader nonce
Just as a friendly reminder, We are exploiting the inital state of LFSR In order to perdict the output of pseudo-random, so that we can decrypt the keystream via the predicted Nonce to gather the key for each sector, in order to operate such as write and read(briefly speaking)
LFSR State Recovery
In this specific type of exploitation, what the attacker is doing is actually firstly caculating every possible LFSR inital state from corresponding KS2 KS3 values and creates a table, And since KS2 KS3 can be decrypted due to the fact that the command for suc2(nT)a and halt is known(According to the Protocols, Read will respone with nR ⊕ ks1 snd suc2(nT) ⊕ ks2). Attacker and search the table with known ks2 and ks3, to recover the inital state of LFSR, which can be simplified into
Listening to the response of the reader when it contains nR ⊕ ks1 snd suc2(nT) ⊕ ks2, attack do not respone, and most of reader will send halt, which is encrypted as halt ⊕ ks3
Recover ks2 and ks3 via known command, since the opcode of halt and suc2(nT), you can recover ks2 and ks3 via the response you listened previously
Use the table to find corresponding LFSR state, and use the knowned LFSR inital state to predict Nonce, and use it to decrypt all the ketstream to find keys
However, knowing one state of LFSR in A specific time K is not enough to get our keys, we will need to use current caculated states to caculate previous states before the reader nonce is fed in which involves:
LFSR Rollback
Firstly, before we start, we have to comprehen the LFSR state fully, for a momont K, as mentioned previously, the LFSR state is given and fixed, in which the states is the bit that this LFSR generates. ever step, LFSR will move these bits and use it as input bit to generate new bit and state.
However, this feature allowed us to rollback to the previous state, since the output bit is only a linear function that takes the previous deleted bit as a parameter.
Additonally, with filter function's fatal flaw (will be discuss later), the most left LFSR bit will not be inputed as filter function, which stands for that even if you don't know the leftest bit. you can obtain it by right side transposing the LFSR state (the rightest bit falls out, the leftest fill by variable 'r') and caculate the filter function(r is not included) to obtain one bit of keystream, which will be used in encrypting the last bit of LFSR.
After that, you can restore the last bit of the LFSR: nR,31, with this bit known, you can caculate the correct state of previous LFSR, and set r to the right value, with that, you can Roll back to previous states, with around 31 rollbacks, before feeding in nT, this LFSR state will be the inital state of the LFSR.
Filter function?
To encrypt, selected bits of the LFSR are put through a filter function f. Exactly which bits of the LFSR are put through f and what f actually is, was not revealed in [NP07]*. Note that the general structure of **CRYPTO1 is very similar to that of the Hitag2. This is a low frequency tag from NXP; the description of the cipher used in the Hitag2 is available on the Internet6. W**e used this to make educated guesses about the details of the initialization of the cipher (see Section 5.1 below) and about the details of the filter function f*
Filter function is used to use the generation of LFSR to generate the keystream which contains our key, however, according to a complex research conducted by the reseachers in the paper, the Filter function seems to contain a fatal flaw: which is it only takes odd place of generation of LFSR (LFSR[1],LFSR[3].....) as a input to generate the keystream. which is something we can exploit at....
Odd Inputs to the Filter Function
As mentioned above, since the filter function only rely on the odd bit of the LFSR, Every bit of the keystream is decided by the odd bit of the LFSR,
Logically, we can focused on the odd bit of the state that will effects the keystream, which futher diminished the amount of possible state that we will search for from 248 into around 65536 possible LFSR states Futhermore, we can use KeyStream to reverselt deduct possible LFSR state, and rollback these states in to the inital state. In this way, only with ks2, there will be 65536 possible LFSR states for us to search. Additionally, This method focused on analysis of current existing data, do not require constant interaction with the reader.
Also LFSR State Recovery method required a 1TB table to find the corresponding state, with the limitation of Odd Inputs to the Filter Function, it only require 8MB and few seconds to obtain the inital state.
How's flipper zero applying?
As the detect reader function, FZ will collect 20 nonce in a session, which can be considered 20 states, using the "Odd Inputs to the Filter Function" attack, we can reverse-engineers the possible LFSR state that generates these nonce. If the right LFSR found, we can use the LFSR Rollback method to rollback to the inital state, thus, using the predicted LFSR to replay and decrypt the communication in that specific session, and finds the keys for sectors.
Subscribe to my newsletter
Read articles from Patrick Peng directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
