Swarm Intelligence Series : Grey Wolf Optimization Algorithm
 Akash Gss
Akash GssTable of contents
- Introduction
- Inspiration for the algorithm
- Convergence
- Breaking down the Hierarchy of the Grey Wolf Optimization Algorithm
- The Steps taken by the Grey Wolf Algorithm
- Exploration vs Exploitation in the Grey Wolf Optimization Algorithm
- Search Parameters Used in the Grey Wolf Optimization Algorithm
- Variations in the Grey Wolf Optimization Algorithm
- Applications of the Grey Wolf Optimization Algorithm
- Limitations of the Grey Wolf Optimization Algorithm
- Code Implementation with MealPy
- Conclusion
- References

The grey wolf optimization algorithm is a population-based meta-heuristic algorithm inspired by the social hierarchy and hunting behavior exhibited by grey wolves in nature. This algorithm mimics the leadership hierarchy and hunting mechanism followed by grey wolves for food to aid in the solving of optimization problems.
Introduction

The grey wolf optimization technique utilizes the overall characteristics exhibited by grey wolf colonies to find the best optimal solutions for the optimization problem at hand. It is one of the metaheuristic optimization techniques inspired by the hierarchy among the wolf family and the special hunting techniques used by grey wolves. This algorithm imitates the overall characteristics of a grey wolf colony and uses the patterns exhibited by a group like this to solve optimization problems in real life. It is used to solve a lot of time-consuming problems like the NP-hard problem and like traveling salesman problem for example. It tends to work for higher dimensions and also reduces the amount of time taken to solve such problems because of its tendency to break down entire complex problems into subsets. The subsets of operation are assigned to every individual agent participating in a manner similar to the duties assigned in the wolf's hierarchy which leads to an optimal solution.
Inspiration for the algorithm
This algorithm is mainly inspired by the social hierarchy distribution of grey wolf packs where the characteristics of every wolf category are different across the colony. A group of wolves known as a pack have different responsibilities assigned to them based on their position in the hierarchy tree.
Alpha Wolf: This is the most superior position in a wolf pack and is looked at as the leader of the pack. This wolf holds the right to command the entire colony of grey wolves.
Beta Wolf: These wolves report to the alpha wolf and are second in line in nature and support the leader in making optimal decisions and more.
Delta Wolf: These wolves are sub-ordinates to the beta wolf providing constant updates to the alpha and beta wolves and are superiors to the last class aka the omega wolves.
Omega Wolf: Omega wolves are mainly responsible for the hunting tasks and are also responsible for taking care of younger wolves.
The Grey Wolf Optimization algorithm is inspired by the hunting behavior of grey wolves, where they work in packs to hunt prey. The algorithm involves maintaining a social hierarchy among the wolves, with alpha, beta, and delta wolves representing the best solutions and omega wolves representing the rest. The optimization process involves updating the positions of all wolves based on the positions of alpha, beta, and delta wolves. This algorithm balances exploration and exploitation to find optimal solutions iteratively.
Convergence
The convergence in this algorithm is crucial to its performance and is also an important factor that helps to determine that the algorithm can effectively navigate the search space in hand to find an optimal or near-optimal solution. This algorithm uses adaptive adjustment strategies to manage convergence and these strategies are designed to fine-tune the algorithm's performance ensuring that it converges to a solution that is not only optimal but also does it in a reasonable amount of time without any premature convergence.
The encircling and hunting mechanisms play a significant role in the convergence of the algorithm. The encircling mechanism, which involves updating the position of the omega wolves based on the positions of the alpha, beta, and delta wolves, is particularly important. The coefficients for this update decrease linearly from 2 to 0 over iterations, and random vectors are introduced to maintain diversity in the search process. This mechanism ensures that the search space is thoroughly explored, and the algorithm does not get stuck in local optima.
The hunting mechanism further aids in convergence by allowing omega wolves to update their positions based on the positions of the alpha, beta, and delta wolves. This mechanism simulates the hunting behavior of grey wolves, where the less dominant wolves learn from the more dominant ones to find the best solution.
Breaking down the Hierarchy of the Grey Wolf Optimization Algorithm
Before we proceed further and dive into the steps or the algorithm of this sophisticated biologically inspired algorithm, let's break into what the hierarchy exactly means in the context of this algorithm and how it will let us interpret and model the grey wolf colony's hierarchical nature in the form of optimal solutions.
Alpha Wolf: This wolf can be termed to be the best and fit solution among all of the possible solutions to the problem and it is in general known as the best possible solution provided to us by the optimization algorithm.
Beta Wolf: This can be termed as the solution that is second to the best solution among all of the other optimal solutions found. This solution will be used in general if the best optimal solution [alpha] does not fit certain conditions.
Delta Wolf: This can be termed to be the third best solution among all of the best possible solutions for the problem. It is evaluated and used if both the first and second solutions do not exactly solve the most optimized use case of this problem.
Omega Wolf: This can be termed as the least optimal solution found so far and it is only compared against the delta solution and if the delta solution is better than it, it'll be discarded.
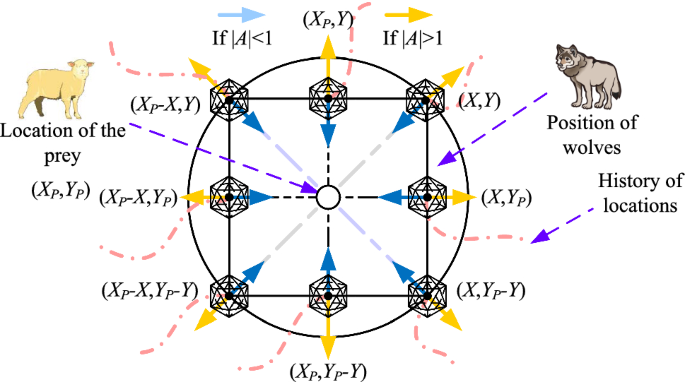
Therefore, in this algorithm, a random number of possible solutions to the problem is validated. All of the possible solutions are validated concerning a standard scale of vectors which in general is denoted as "A".
So if A>1 the possible solutions diverge from the optimal solution of the problem and A<1 then all the possible solutions converge towards the optimal solution to find the best fittest solution to the problem.
Once the best fittest solution is determined the algorithm stops iterating and the best possible solutions to the problem are ranked suitably and from the rankings provided the solutions are validated. In most cases, the best fittest solution is used and in rare cases, the second-best optimal solution is chosen for certain problems over the best fittest solution.
The Steps taken by the Grey Wolf Algorithm
The Grey Wolf Optimization Algorithm is heavily inspired by the social hierarchy and hunting mechanism of grey wolves in nature. It is a population-based meta-heuristic optimization algorithm that involves 4 levels - alpha, beta, delta, and omega wolves with every level having a different level of dominance over the peak with alpha having the most while omega having the least. The algorithm's steps to solve a problem can be broken down into 3 main phases - searching for prey, encircling the prey, and attacking the prey.
Searching for Prey(Exploration): In this phase, the omega wolves, which are the least fit members of the pack, search for potential solutions by diverting from the positions of the alpha, beta, and delta wolves. This divergence of them is achieved through a vector with random values in the range of -1 to 1 forcing the omega wolves to search the search space more widely. The Algorithm employs a vector with random values in the range [0,2] to provide random weights for the prey, emphasizing exploration and avoiding local optima. This component is mainly utilized to maintain diversity and exploration throughout the exploration process, especially during the final iterations where a local optimum that could potentially be a suboptimal solution could occur.
Encircling Prey: After the exploration phase, the omega wolves encircle the potential solutions and this encircling behavior is mathematically modeled by updating the positions of the omega wolves based on the positions of the alpha, beta and delta wolves with coefficients that range between 0-2 over the iterations performed. This mechanism is mainly used to ensure that the search space is thoroughly explored and the algorithm doesn't get stuck in a locally optimal solution. This phase is extremely important to refine the search process around the best solutions found by the alpha, beta, and delta wolves.
Attacking Prey: The final phase involves the attack process where the omega wolves attack the prey that is represented algorithmically by updating their positions based on the positions of the other wolves in the hierarchy - alpha, beta, and delta wolves. This phase simulates the hunting behavior of grey wolves, where the less dominant wolves learn from the more dominant ones to find the best solution. This algorithm updates the positions of the omega wolves in every iteration, based on the relative positions of the other higher-level wolves which are known to have better knowledge about the potential location of the prey than the omega wolves.
This algorithm tends to maintain a balance in general for the search process and it encourages exploration by diverging one specific hierarchy of the wolves [omega] from the prey while also ensuring that they do not deviate too much from the solution which could lead to the loss of valuable information.
This algorithm tends to update the positions of the omega wolves in every iteration based on the positions of alpha, beta, and delta wolves which are considered to have better knowledge about the potential location of the prey. Therefore, The process of the algorithm's way to hunt for solutions involves exploration, encircling, and attacking phases, which are crucial for navigating the search space efficiently and converging to optimal solutions.
Exploration vs Exploitation in the Grey Wolf Optimization Algorithm
The Grey Wolf Optimization algorithm iteratively updates the positions of all wolves and their fitness values, gradually converging towards an optimal or near-optimal solution. Throughout the optimization process, the algorithm maintains a balance between exploration and exploitation. It encourages exploration by forcing the wolves to diverge from the prey, while also ensuring that the wolves do not deviate too far from the prey, which could lead to the loss of valuable information.
Let's break down how exactly this process takes place in this algorithm,
Exploration: The omega wolves that represent the least fit members of the pack are tasked with exploration and search for potential solutions diverging from the positions of alpha, beta, and delta wolves. They search for potential solutions by first diverging from the alpha, beta, and delta wolves and this divergence is achieved using a vector parameter with random values in the range of -1 to 1. This parameter is crucial as it forces the omega wolves to explore the search space more widely and additionally, a vector C with random values in the range of 0-2 provides random weights for the prey, emphasizing exploration and avoiding local optima. This component is also important to maintain diversity and exploration throughout the optimization process, especially towards the end when the local optima might occur.
Exploitation: After the exploration phase, the algorithm shifts focus to exploitation. The Omega wolves encircle the potential solutions, which are mathematically modeled by updating their positions based on the positions of the alpha, beta, and delta wolves with coefficients decreasing from 2 to 0 over the iterations. This encircling mechanism ensures that the search space is thoroughly explored, and the algorithm does not get stuck in local optima. The encircling phase is critical for refining the search around the best solutions found by the alpha, beta, and delta wolves.
Search Parameters Used in the Grey Wolf Optimization Algorithm
This algorithm depends on several parameters to guide its optimization problems. The Parameters used in this algorithm tend to play a crucial role in making sure that the algorithm can effectively navigate the search space to search for an optimal solution and it is also important for controlling the behavior of the algorithm or how exactly the algorithm follows the process of searching. The parameters used are -
Population Size: The number of grey wolves in the pack, determines the diversity of solutions considered in every iteration. A larger population size can lead to a wider exploration of the search space but may also increase computational complexity.
Number of Iterations: The maximum number of iterations in the algorithm will run before it stops. This is crucial for balancing the exploration vs exploitation process in this algorithm particularly.
Coefficients for position update: These coefficients are used for the encircling and hunting mechanisms followed by this algorithm and are used to control how the positions of the hunters aka the omega wolves are updated based on the alpha, beta, and delta wolves. The coefficients range between 0-2 in value in general and they are determined by the positions of the hunting wolves in a relative manner.
Random Vector [A]: This parameter is used to force the hunters or the omega wolves to explore the search space more widely during the exploration phase and is also used to maintain diversity in the search process and prevent the algorithm from getting stuck in local optima. Its range is between -1 to 1.
Random Weight Vector [C]: This vector is used to provide random weights for prey, emphasizing exploration and avoiding local optima. This component is particularly important in the encircling phase, where the omega wolves encircle the potential solutions based on the positions of the alpha, beta and delta wolves.
Boundary Constraints: The algorithm must consider the boundaries of the search space to ensure that the solutions generated do not fall outside the defined limits. This is crucial for maintaining the feasibility of the solutions.
Fitness Function: The function used to evaluate the quality of the solutions. The algorithm aims to maximize or minimize this function, depending on the problem being solved.
Variations in the Grey Wolf Optimization Algorithm
Improved Grey Wolf Optimization Algorithm: This variation was introduced to improve the original algorithm. This variation includes modifications aimed at enhancing the algorithm's performance in finding optimal solutions. This variation includes adjustments to the exploration and exploitation mechanisms as well as the hunting behavior of the wolves. These adjustments help in refining the search process and improving the efficiency of the algorithm.
Chaotic Grey Wolf Optimization: This variation involves chaotic maps into the position update equations of the wolves which are used to induce a randomness to the search process to avoid local optima and improve the algorithm's search capabilities.
Multi-Objective Grey Wolf Optimization: The standard algorithm is designed for single objective optimization algorithms and this improved algorithm can handle problems with multiple objectives with each having different priorities. This requires modifying the fitness evaluation process mainly.
Hybrid Grey Wolf Optimization Algorithm: This approach combines this algorithm with other algorithms like the Particle Swarm Optimization algorithm and the Genetic Algorithm and leverages the strengths of this algorithm to form a better-hybridized version of the GA or PSO algorithm.
Adaptive Grey Wolf Optimization Algorithm: This algorithm addresses some limitations of the original algorithm like it being susceptible to the local optima because it primarily relies on the initial 3 levels of wolves to share the information which can lead to a lack of diversity and this algorithm introduces a dynamic way of adjusting the parameters which prove to be crucial to maintain diversity and premature convergence.
Applications of the Grey Wolf Optimization Algorithm
Path Planning: This algorithm has been adapted for path planning in mobile navigation systems and helps address challenges like avoiding obstacles and the local optima.
Control systems: It is used heavily in control systems to regulate processes and to make the system more streamlined and efficient in general.
Thermal systems: It is used in thermal power systems to optimize the production process of energy and its consumption as well.
Limitations of the Grey Wolf Optimization Algorithm
The Grey Wolf algorithm despite being effective and efficient in solving optimization problems has certain limitations which can affect its performance and applicability in different areas. The limitations include
Convergence Speed: The speed of convergence of this algorithm to solve certain problems may prove to be less satisfactory in nature. It may potentially take a longer time to reach an optimal or a near-optimal solution for certain problems as compared to the other biological metaheuristic algorithms available.
Lower Accuracy: This algorithm tries to find the optimal solution in general only when the best possible solution falls under the territory of the optimal solution. This makes the algorithm give lower accuracies sometimes.
High Parameter Sensitivity: This algorithm is highly sensitive to the parameters used and incorrect parameter settings can often lead to suboptimal performance or failure of convergence.
Limited Generalization: This algorithm may not be able to generalize well across a wide range of optimization problems and its effectiveness can vary depending on the specific characteristics of the problem at hand.
Lack of Adaptability to Non-Linear Problems: This algorithm could not adapt as well to nonlinear problems and may be less optimal for problems exhibiting characteristics like being complex, possessing a non-convex search space, and high dimensionality.
Code Implementation with MealPy
This algorithm can be implemented with the MealPy Library using Python like so
import numpy as np
from mealpy.swarm_based.GWO import BaseGWO
def fitness_function(solution):
return np.sum(solution**2)
problem_dict1 = {
"fit_func": fitness_function,
"lb": [-10, -15, -4, -2, -8],
"ub": [10, 15, 12, 8, 20],
"minmax": "min",
}
epoch = 1000
pop_size = 50
model = BaseGWO(problem_dict1, epoch, pop_size)
best_position, best_fitness = model.solve()
print(f"Solution: {best_position}, Fitness: {best_fitness}")
Conclusion
Among the various optimization techniques, the grey wolf technique tries to find the optimal solution uniquely by following the overall principles of grey wolf hunting. The grey wolf optimization is a better choice for higher dimensional data and certain problems like the traveling salesman problem. The overall algorithm produces the nearest optimal solution when compared to the best optimal solution which can be validated and if required can be optimized further as optimization of the grey wolf technique can be done with a fewer number of parameters.
References
https://analyticsindiamag.com/a-complete-overview-of-grey-wolf-optimization-technique/
Subscribe to my newsletter
Read articles from Akash Gss directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by