Leetcode 59 Spiral Matrix II

Given a positive integer n, generate an n x n matrix filled with elements from 1 to n^2 in spiral order.

Example 1:

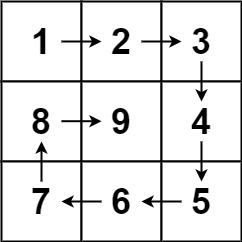
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

Example 2:

Input: n = 1
Output: [[1]]

Constraints:

• 1 <= n <= 20

Understanding the Problem:

The problem statement asks for a function that, given a positive integer n, generates an n x n matrix filled with elements from 1 to n^2 in a spiral order. To tackle this problem efficiently, it's crucial to comprehend the nature of the spiral traversal within the matrix.

To identify recurring patterns, consider that any n x n square can be traversed in a circular manner, consisting of four sides: top, left, right, and bottom. The number of such circular traversals, or "loops," can be determined by n/2. For odd values of n, the middle number requires special handling.

For instance, in a 3 x 3 square:

# Given 3 * 3 Square, rotate in spiral order 
- TOP
    [0, 0] = 1; [0, 1] = 2;

- RIGHT
    [0, 2] = 3; [1, 2] = 4;

- BOTTOM
    [2, 2] = 5; [2, 1] = 6;

- LEFT
    [2, 0] => 7; [1, 0] = 8;

- MIDDLE
    [1, 1]

Finding the solution

The solution utilises the above understanding to systematically fill the matrix in a spiral order. By iteratively traversing the four sides of each loop and incrementally filling the matrix with integers, the algorithm constructs the desired spiral matrix efficiently.

const generateMatrix = function(n) { 
    let loop = Math.floor(n / 2);
    let mid = Math.floor(n / 2);
    let count = 1;
    let offset = 1;
    let x = 0;
    let y = 0;
    let result = new Array(n).fill(0).map(() => (new Array(n).fill(0)));
    while (loop--) {
        let col = y;
        let row = x;
        //TOP
        for (; col < n - offset; col++) {
            result[row][col] = count++;
        };
        //RIGHT
        for (; row < n - offset; row++) {
            result[row][col] = count++;
        };
        //BOTTOM
        for (; col > y; col--) {
            result[row][col] = count++;
        };
        //LEFT
        for (; row > x; row--) {
            result[row][col] = count++;
        };
        x++;
        y++;
        offset++;
    }
    if (n % 2 !== 0) {
        result[mid][mid] = n * n;
    };
    return result;
}

Complexity analysis

Each of the four loops iterates n - offset times. The total number of loops is n/2.

Therefore, the worst-case time complexity of this solution is O(n^2).

Conclusion

In conclusion, the provided algorithm efficiently generates a spiral matrix by systematically traversing the matrix in a spiral order and filling it with consecutive integers. By understanding the underlying pattern of traversal and employing systematic loop operations, the algorithm achieves the desired functionality within a time complexity of O(n^2).