How to manually convert decimal numbers to binary and vice versa
 Maxat Akbanov
Maxat Akbanov
Sometimes you won't have a calculator right beside you and you will be forced to convert decimal numbers to binary or vice versa by hand. For example, you may need to calculate the network and host IP addresses by using subnet mask. In this article I provide description of several techniques that you can keep in your arsenal.
Convert decimal to binary: Dividing by 2 Technique
Converting a decimal number to binary by hand involves dividing the number by 2 and keeping track of the remainders at each step. Here's a step-by-step guide on how to do it:
Divide the number by 2. Write down the quotient and the remainder.
Use the quotient as the new number to divide by 2. Again, write down the new quotient and the remainder.
Repeat the process until the quotient is 0.
The binary number is the sequence of remainders read from bottom to top.
Example: Convert 13 to Binary
Let's convert the decimal number 13 to binary following these steps:
13 divided by 2 gives a quotient of 6 and a remainder of 1.
6 divided by 2 gives a quotient of 3 and a remainder of 0.
3 divided by 2 gives a quotient of 1 and a remainder of 1.
1 divided by 2 gives a quotient of 0 and a remainder of 1.
Reading the remainders from bottom to top, you get 1101. So, 13 in decimal is 1101 in binary.

Practice Example
You can practice by converting a different decimal number, say 45, into binary using the same steps:
Divide 45 by 2, keep the quotient and the remainder.
Continue dividing the quotient by 2 until you get a quotient of 0.
Collect all the remainders and read them from bottom to top to get your binary number.
This method works for any positive decimal number and is a fundamental principle in computer science for understanding how numbers are represented in binary within computing systems.
To check the answer you can use bdconvert tool:
bdconvert --decimal 45
Convert decimal to binary: Ruler method
Another approach involves recognizing and adding the largest powers of 2 within the decimal number, which could be seen as a "ruler" approach if you list the powers of 2 (like markings on a ruler) and then subtract them successively from the decimal number until you reach 0.
Conceptual Overview of a Ruler-like Method
List Powers of 2: Write down the powers of 2 in descending order that are less than or equal to the decimal number you're converting. This could be likened to using a "ruler" where each mark represents a power of 2.
Subtract Powers of 2: Start from the largest power of 2 and subtract it from the decimal number if possible (i.e., if the remainder is non-negative). Mark a '1' for each power of 2 you can subtract, and a '0' if you can't.
Repeat Until 0: Continue subtracting with the next lower power of 2 until you reduce the decimal number to 0. The sequence of '1's and '0's gives you the binary representation.
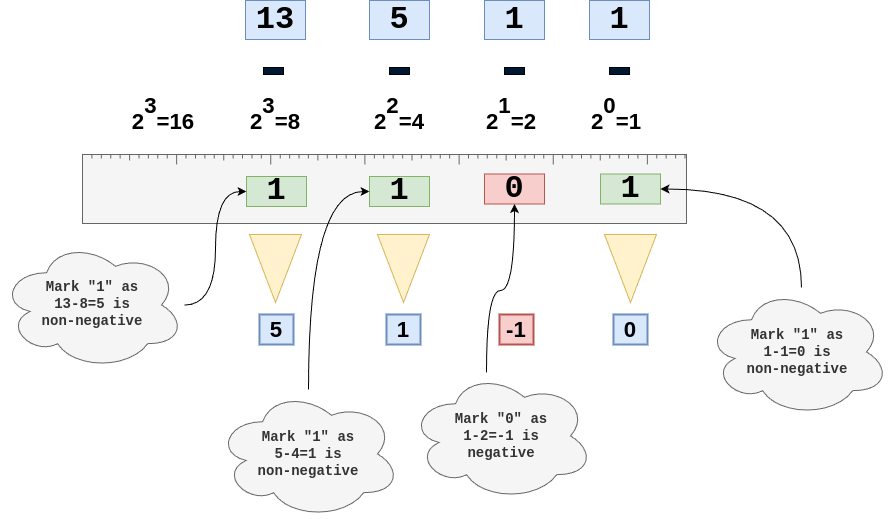
Table of Powers of 2
Here's a table showing the powers of 2. This range covers most common uses, including binary conversions and understanding computer memory and storage capacities.

This table is helpful for understanding binary numbers, calculating storage capacities, and many other applications in computing and digital electronics.
Convert Binary to Decimal
Converting a binary number to decimal involves understanding that each digit in a binary number represents a power of 2, based on its position. The rightmost position represents (2^0), the next position to the left represents (2^1), and so forth. To convert a binary number to its decimal equivalent, follow these steps:
Write down the binary number. Break it into individual digits for analysis.
Assign power values to each digit. Starting from the right (least significant bit), assign powers of 2 to each digit. The rightmost digit is (2^0), the next is (2^1), then (2^2), and so on, moving to the left.
Multiply each binary digit by its power of 2. If the digit is 1, you multiply it by its corresponding power of 2. If it's 0, the result is simply 0 (since anything times 0 is 0).
Add up all the results. The sum of these products gives you the decimal number equivalent.
Example: Convert 1101 to Decimal
Let's use the binary number 1101 as an example:
The rightmost digit (1) is (2^0), which is 1. Since the binary digit is 1, we have (1 \times 2^0 = 1).
The next digit to the left (0) is (2^1), which is 2. The binary digit is 0, so (0 \times 2^1 = 0).
Moving one more digit to the left (1) is (2^2), which is 4. The binary digit is 1, so (1 \times 2^2 = 4).
The leftmost digit (1) is (2^3), which is 8. The binary digit is 1, so (1 \times 2^3 = 8).
Now, add all these results together: (1 + 0 + 4 + 8 = 13).
So, the binary number 1101 is equal to 13 in decimal.

This process is fundamental in computing and digital electronics, as it bridges human-readable numbers (decimal) with machine-readable numbers (binary).
To check the conversion use bdconvert tool:
bdconvert --binary 1101
References:
Subscribe to my newsletter
Read articles from Maxat Akbanov directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Maxat Akbanov
Maxat Akbanov
Hey, I'm a postgraduate in Cyber Security with practical experience in Software Engineering and DevOps Operations. The top player on TryHackMe platform, multilingual speaker (Kazakh, Russian, English, Spanish, and Turkish), curios person, bookworm, geek, sports lover, and just a good guy to speak with!