Swarm Intelligence Series : Ant Colony Optimization
 Akash Gss
Akash GssTable of contents
- Introduction
- Inspiration
- Convergence
- Algorithm
- Specialty of the Algorithm
- Search Parameters of the ant colony optimization algorithm
- Variations of the Ant Colony Optimization Algorithm
- Applications of the Ant Colony Optimization Algorithm
- Limitations of the Ant Colony Optimization Algorithm
- Code Implementation With Mealpy
- Conclusion

The Ant Colony Optimization Algorithm is a computational technique that is heavily inspired by the behavior of ants in finding the shortest path to the food sources from the colony.
Introduction
The Ant Colony Optimization Algorithm is a probabilistic technique used to solve metaheuristic problems and it is a part of the swarm intelligence class of algorithms. The main goal of this algorithm is to search for the optimal path from the colony of the ants to the food source similar to how the shortest search in a graph is performed. This is a fascinating algorithm in computer science heavily modeled behind the foraging behavior exhibited by ants. It excels in solving complicated shortest-path problems like the traveling salesman problem and is more typically found in graph networks.
Inspiration
Imagine a bustling colony of ants, diligently searching for food. The journey they embark on is a fascinating display of collective intelligence in nature. Every ant explores its surroundings in a random fashion, leaving behind a chemical trail known as pheromones which are like bread crumbs. As these ants return to the nest, they deposit more pheromones on the paths that lead them to the food sources in a much quicker manner, and over time this collaborative effort creates a strong pheromone trial on the shortest path, guiding other ants towards an efficient route.
This led to the foundation of this algorithm where the algorithm used "artificial ants" to explore a search space represented in the form of a graph. Initially, all paths have the same probability of being chosen. However, as the ants find better solutions they leave a "digital pheromone trial" that increases the likelihood of other ants following the same path in future iterations. This collaborative exploration and adaptation carried out by ants allow this algorithm to find increasingly optimal solutions for complex shortest-path problems in sophisticated graph networks over time.
Convergence
The convergence of this algorithm is a complex topic with ongoing research. While not all of the variants of this algorithm guarantee convergence to the global optimum, there has been significant progress made in understanding and ensuring convergence in different contexts where this algorithm has been used. The Ant colony optimization algorithm can tend to get stuck in a locally optimum solution when they find a good solution and not the best one and this is because of the pheromone trail left behind by them which can become too concentrated or "strong" in a suboptimal solution leading the other ants as a part of the colony astray and preventing them from exploring better alternative solutions. The convergence of this algorithm can also depend on the search parameters picked for the specific implementation.
Algorithm
Initialization: The problem in hand is first modeled in the form of a graph where the nodes represent the tasks and the edges represent the solutions in the graph. An initial pheromone level is assigned to each edge in the graph. Other parameters are set, including the number of ants, pheromone evaporation rate, and heuristic weight.
Solution Construction: Every ant starts at its designated start note and iteratively every ant chooses the next node to be visited by considering the pheromone level and a heuristic factor associated with each unvisited neighbor. Higher pheromone levels and lower heuristic values generally make an edge much more attractive. And, a small amount of randomness is also added to prevent premature convergence and ensure the exploration of diverse paths.
Solution Evaluation: Every ant's solution is evaluated based on a fitness function that measures the quality of the chosen path, typically aiming to optimize distance, time, cost, or any other relevant metric to solve the problem at hand.
Pheromone Update: Based on the quality of the solutions gathered, the ants update the pheromone levels on the edges they've traversed or visited and the ants with better fitness values tend to deposit more pheromone on the edges used, strengthening the paths for future exploration and increasing the chances of the other ants picking these paths. The existing pheromone levels decay over time to prevent the algorithm from getting stuck on outdated information and encourage the exploration of new paths.
Iterations: This allows the ants to learn from each other and progressively get better and improve the solutions discovered over a period of time.
Termination: The algorithm terminates finally when a stopping criterion is met like reaching the maximum number of iterations or finding a sufficiently good solution for the optimization or meta-heuristic problem or the shortest path problem on a graph that is in hand.
Specialty of the Algorithm
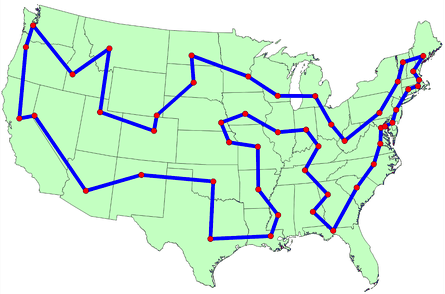
The Ant Colony Optimization algorithm is particularly adept at solving graph-based problems, such as finding the shortest path through a network, optimizing routes for delivery vehicles, and even solving complex optimization problems like the Traveling Salesman Problem (TSP). This capability is due to the algorithm's ability to mimic the behavior of ants in finding paths from their colony to food sources, which can be translated into finding optimal paths through graphs.
And, the way it does it -
Pheromone Trails: It uses pheromone trails to guide the search process. Each solution (path) is associated with a pheromone trail, which ants deposit on the edges of the graph representing the solution space. The amount of pheromone deposited is proportional to the quality of the solution, with better solutions attracting more pheromones.
Artificial Ants: These are computational agents that simulate the behavior of real ants. They move through the graph, constructing solutions by following edges based on the pheromone levels and the attractiveness of the next state.
Local Search and Exploration: It balances local search and exploration. Local search allows the algorithm to refine the solutions found by the ants, while exploration ensures that the algorithm does not get stuck in local optima.
Search Parameters of the ant colony optimization algorithm
Number of Ants (n): This parameter determines the number of virtual ants exploring the search space. Increasing the number of ants generally allows for better exploration and diversification but can lead to an increase in computational cost.
Pheromone Evaporation Rate (ρ): This controls how quickly pheromone levels may decay on the edges or the paths picked over time. A higher rate of evaporation encourages the exploration of new paths while a lower rate emphasizes previously found good paths. Finding the right balance is crucial to avoid stagnation on suboptimal solutions.
Heuristic Weight (α): This parameter determines the relative importance of the heuristic factor in the ant's decision-making process for choosing the next node. A higher α value emphasizes the heuristic, leading ants towards shorter paths or other favored options based on the problem.
Pheromone weight (β): This parameter determines the relative importance of the pheromone level in the ant's decision-making process. A higher β value increases the influence of pheromones, guiding ants towards paths with higher pheromone concentrations.
Initial pheromone level (τ⁰): This parameter assigns an initial, small value of pheromone to all edges in the graph at the beginning of the algorithm. It affects the initial exploration and can be adjusted based on the problem characteristics.
Optional Pheromone Upper Bound: This parameter is used optionally to limit the maximum pheromone level possible at any edge of the graph preventing single paths from dominating the search and encouraging more amount of exploration.
Variations of the Ant Colony Optimization Algorithm
Elitist Ant Variant: This is a variation of this algorithm that incorporates an elitist mechanism to ensure that the best solutions found by any ant are given priority in the next iteration. This mechanism is kind of like a greedy strategy and it helps to escape the locally optimum solutions and maintain diversity in the population of the ants the best solution found by any ant is selected as the best solution of the iteration and its pheromone is not updated, ensuring its persistence in the next generation.
Max-Min Ant Variant: This is designed to control the range of pheromone levels, which is crucial for maintaining diversity in the search process and preventing premature convergence. It introduces a mechanism to adjust the pheromone update rule, ensuring that the pheromone levels do not deviate too much from the average. This helps in maintaining a balance between exploration and exploitation allowing the algorithm to explore new areas in the solution space while also exploiting known good solutions.
Rank-Based Ant Update Variant: This variation employs a more controlled trial of the pheromone update strategy, setting upper and lower bounds on the levels of the pheromone possible on every edge. This helps introduce much-needed constraints as needed and prevent stagnation. It also ensures the diverse exploration of the search space over time.
Probabilistic Pheromone Update Variant: This introduces a probabilistic approach to pheromone updates where the amount of pheromone deposited on a solution's path is not fixed but is determined by a probability distribution. This can help in introducing randomness into the update process, which can be beneficial in exploring the solution space and avoiding getting stuck in local optima.
Hybrid Ant Colony Optimization algorithm: This combines the original variant of the algorithm with other optimization algorithms or heuristics to leverage the individual strengths of the multiple options considered. This algorithm for example can be combined with the Genetic Algorithm to introduce mutation and crossover operators, enhancing the diversity of the solutions generated. A few more algorithms it is hybridized against popularly are the tabu search algorithm and the simulated annealing algorithm used to escape local optima and avoid premature convergence.
Multi-Objective Ant Colony Optimization Algorithm: This extends the original version to handle multiple-objective optimization problems. It introduces a mechanism to evaluate and balance the picking of multiple objectives or solutions allowing the algorithm to find a set of solutions that are not only optimal but also Pareto-optimal.
Applications of the Ant Colony Optimization Algorithm
Data Mining: This algorithm is used for feature selection in data mining and is used to identify more relevant features for the classification tasks.
Routing and Network Optimization: It is used heavily for graph-based problems like wireless sensor networks to enable more efficient communication amongst the sensory nodes residing in the network.
Distributed Information Retrieval: This algorithm is used in distributed information retrieval systems to optimize query processing and retrieval strategies employed.
Protein Folding: This when modeled in the form of a graph can be solved with the ant colony optimization algorithm where the nodes represent amino acids in the protein and the edges represent potential interactions between them this algorithm is utilized to find the optimal folding path for the proteins which is critical to understand protein function and disease.
Fleet Management: This algorithm can be used heavily for finding the most efficient routes for a fleet delivery provider to arrange his vehicles in order to deliver goods to a set of customers while minimizing the total time spent traveling and this is simulated with the help of ants traversing through a graph representing cities and the routes that can be taken with the goal of minimizing the total distance traveled by all of the vehicles while finishing their designated tasks.
Limitations of the Ant Colony Optimization Algorithm
Convergence to Suboptimal Solutions: This algorithm may face challenges in finding the globally optimum solution in complex problem spaces with multiple local optima and its reliance on pheromone trials and local information exchange can sometimes lead to premature convergence to suboptimal solutions, rather than the best optimal solution.
Sensitivity to Parameter Settings: The performance of this algorithm is very heavily dependent on the tuning of its parameters and the parameters specifically the pheromone evaporation rate and the balance between exploration and exploitation play a crucial role in determining the algorithm's convergence speed and the quality of the solutions produced by it.
Computational Complexity: This algorithm can start becoming computationally complex as the number of iterations and the ants participating increase. This can make the algorithm less suitable for handling large problem instances or for real-time or time-critical applications where execution time and memory requirements need to be minimized.
Limited Capability to Handle Dynamic Environments: This algorithm may struggle with sudden and drastic changes in the problem space and might require additional mechanisms or modifications to effectively handle rapidly changing scenarios.
Code Implementation With Mealpy
This algorithm can be implemented using the Python Library named MealPy
import numpy as np
from mealpy import FloatVar, ACOR
def objective_function(solution):
return np.sum(solution**2)
problem_dict = {
"bounds": FloatVar( lb=(-10.,) * 30, ub=(10.,) * 30, name="delta"),
"obj_func": objective_function,
"minmax": "min",
}
model = ACOR.OriginalACOR(epoch=1000, pop_size=50, sample_count = 25, intent_factor = 0.5, zeta = 1.0)
g_best = model.solve(problem_dict)
print(f"Solution: {g_best.solution}, Fitness: {g_best.target.fitness}")
print(f"Solution: {model.g_best.solution}, Fitness: {model.g_best.target.fitness}")
Conclusion
In conclusion, the Ant Colony Optimization algorithm stands as a remarkable example of nature-inspired optimization, demonstrating remarkable efficiency and effectiveness in solving complex optimization problems. Its core principles, inspired by the behavior of ants in finding the shortest path to food sources, have been adapted to tackle a wide array of optimization challenges, from routing and scheduling to machine learning and data analysis.
The simplicity and adaptability of it make it a versatile tool for problem-solving across different domains. It has proven particularly adept at handling graph-based optimization problems, such as the Traveling Salesman Problem and Vehicle Routing Problem, where it has consistently delivered near-optimal solutions. The algorithm's ability to balance exploration and exploitation, guided by the pheromone trails left by previous solutions, allows it to navigate the solution space efficiently, avoiding pitfalls like local optima and converging towards global optimum solutions.
However, it's important to recognize the algorithm's limitations, such as its sensitivity to parameter settings and its computational complexity in handling large problem instances. Despite these challenges, the algorithm's potential for adaptation to dynamic environments and its robustness in producing high-quality solutions make it a valuable asset in the toolkit of optimization algorithms.
Subscribe to my newsletter
Read articles from Akash Gss directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

