Demystifying Tree Data Structure: A Journey into the World of Hierarchical Structures
 Ayoola Adewale
Ayoola Adewale
Ever heard of trees in the world of programming? No, not the ones in your backyard but a fascinating concept that helps organize information in the digital world using a tree-like structure.
Whether you're a coding newbie or a seasoned developer, understanding the basics of tree structures can open up exciting possibilities in organizing data and creating smart algorithms. In this journey, we'll simplify the complex world of trees, starting from the basics and going even further. We'll break down the intricate details into easy-to-understand parts, making it a breeze to grasp.
So, get ready to explore the simplicity, elegance, and usefulness of tree structures in the coding universe. Welcome to "Demystifying Tree Data Structure: A Journey into the World of Hierarchical Structures! Let's dive in.
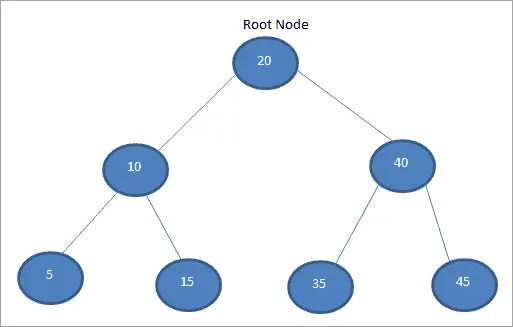
A tree data structure is a hierarchical structure that is used to represent and organize data in a way that is easy to navigate and search. Trees can have zero or more child nodes, so we have a parent-child relationship that is unidirectional.
A tree usually starts with a single root or parent node and every child of the tree descends from that root node; it's like an inversed tree. Within a tree, we can have sub-trees; from the diagram above, the sub-trees are [10, 5, 15] and [40, 35, 45]. Also, we have leaf nodes which are nodes that resides at the end of a branch in a tree and does not have any descendants; from the diagram above, the leaf nodes are [5, 15, 35, 45].
Tree data structures are of paramount importance as they find everyday applications, ranging from representing family trees to organizing the structure of web pages to representing the structure of a program or code.
One way to represent the structure of a program or code is through an abstract syntax tree (AST). An abstract syntax tree (AST) is a data structure used in computer science to represent the structure of a program or code snippet. It is a tree representation of the abstract syntactic structure of text (often source code) written in a formal language.
In the context of web development, the Document Object Model (DOM) tree plays a pivotal role. It serves as a structured and standardized interface, allowing web browsers and JavaScript to seamlessly interact with and manipulate the content of a web page.
BINARY TREE
A Binary Tree Data Structure is a hierarchical data structure in which each node has at most two children, referred to as the left child and the right child. It is commonly used in computer science for efficient storage and retrieval of data, with various operations such as insertion, deletion, and traversal.
class Node {
constructor(value) {
this.left = null;
this.right = null;
this.value = value;
}
}
Several rules and properties govern binary trees. Here are some fundamental rules applied to binary trees:
Each node in a binary tree contains a data element, often referred to as the "key" or "value."
Nodes may have zero, one, or two children.
Each child node can only have one parent.
Binary trees are categorized into several special types based on their structural or functional properties. Here are some common types of binary trees:
Complete binary tree: A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as left as possible.
A / \ B C / \ D EPerfect binary tree: A perfect binary tree is a specific type of binary tree in which all levels are completely filled, and all leaf nodes are at the same level. Additionally, every internal node has exactly two children. This means that every level of the tree is fully occupied, and the tree is perfectly balanced.
This type of binary tree is really efficient and desirable. When binary trees are perfect they have some interesting properties:
On each level, the total number of nodes doubles as we move down the tree.
The total number of nodes on the last level is equal to the number of nodes on other levels plus 1.
A
/ \
B C
/ \ / \
D E F G
BINARY SEARCH TREE
A binary search tree (BST) is a fundamental data structure in computer science that organizes and stores data in a way that enables efficient search, insertion, and deletion operations. The defining characteristic of a binary search tree is the ordering of its nodes.
Some fundamental rules applied to binary search trees:
The left child of a node contains a value that is less than or equal to the parent node's value.
The right child of a node contains a value that is greater than the parent node's value.
This rules ensures that searching for a specific value can be done efficiently by traversing the tree based on the comparison of values.
Some key features and operations associated with binary search tree:
Search/Lookup Operation: The search operation in a BST is logarithmic in time complexity, i.e., O(log n) since at each step, the search space is effectively divided in half. This makes BSTs particularly efficient for search operations.
Insertion Operation: Inserting a new element into a BST involves comparing the value of the new element with the values of nodes as it traverses the tree. Based on the comparisons, the new node is then appropriately placed as a left or right child.
Deletion Operation: There's a bit of tough logic that happens when deleting a node from a BST, this operation requires careful consideration of its children. If the node has no children, it can be removed directly. If it has one child, the child takes its place. If it has two children, it can be replaced with its in-order successor (or predecessor), maintaining the BST properties.
// Binary Search Tree
// 50
// / \
// 33 65
// / \ / \
// 15 37 60 78
For example, let's say we want to delete 65. First, from the parent/root node we need to get to 65, and then decided which node is going to take its place. In this case, the right child node (78) is greater than left child node (60), so the right child node (78) replace 65 then 60 becomes the left child node of 78.
BALANCED VS UNBALANCED BST
A balanced BST is a tree in which the heights of the left and right subtrees of every node differ by at most one. This ensures that the tree is relatively evenly distributed and resembles a well-structured hierarchy. Operations such as search, insertion, and deletion in a balanced BST have an average time complexity of O(log n) as each comparison reduces the search space by half, where n is the number of nodes.
An unbalanced BST is a tree in which the heights of the left and right subtrees of some nodes differ significantly. In extreme cases, an unbalanced BST can degenerate into a linked list, where all nodes have only one child. Operations on an unbalanced BST can have a worst-case time complexity of O(n), where n is the number of nodes. Unbalanced trees may occur due to poorly ordered insertions or deletions without proper rebalancing.
How do we balance a tree? Ensuring the balance of a tree involves preserving its structural integrity, thereby guaranteeing that search, insertion, and deletion operations retain efficiency with a logarithmic time complexity. Algorithms such as AVL trees and Red-Black trees ensure that our binary search tree remains balanced.
PROS AND CONS OF A BST
PROS
Searching in a well-balanced BST has a time complexity of O(log n), making it efficient for large datasets.
The ordering of keys in a BST provides a natural way to traverse and process data in a sorted order using in-order traversal.
BSTs are relatively straightforward to implement, and their logic is easy to understand, making them suitable for a variety of applications.
CONS
It has no O(1) operation because we always have to do some traversal down through the tree for any sort of operation.
If the tree becomes unbalanced (skewed), the performance of operations degrades to O(n), resembling a linked list. This is a significant drawback.
The efficiency of a BST is highly dependent on the order in which elements are inserted. Poor insertion order can lead to unbalanced trees.
Deleting a node with two children in a BST can be complex and may require additional steps, such as finding the in-order successor or predecessor.
BST vs. Hash Tables vs. Array
BST:
Efficient search with O(log n) time complexity in balanced trees.
Ordered structure, suitable for maintaining order.
More memory-efficient than hash tables.
Hash Tables:
Constant time complexity (O(1)) on average for search, insertion, and deletion.
Unordered structure, efficient for quick access.
Can consume more memory due to handling collisions.
Arrays:
Efficient for indexed access with O(log n) for sorted arrays.
Ordered by index, suitable for quick indexed access.
Memory-efficient for static datasets.
Note: BSTs are efficient for ordered data and dynamic datasets, hash tables excel in quick access scenarios, and arrays are optimal for indexed access and static datasets.
In wrapping up our discussion on tree data structures, let's switch gears and have some fun! How about we roll up our sleeves and build our own binary search tree? Ready to dive in?
class Node {
constructor(value) {
this.left = null;
this.right = null;
this.value = value;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
// validate inputted value
if (typeof value !== "number") {
return "Invalid input";
}
// check if root node is empty
if (this.root === null) {
this.root = newNode;
return this;
} else {
let currentNode = this.root;
while (true) {
if (currentNode.value > newNode.value) {
// GO LEFT
// Check if the left side of the current node is empty
if (!currentNode.left) {
currentNode.left = newNode;
return this;
}
// if it's not empty
// update the current node
currentNode = currentNode.left;
} else if (currentNode.value < newNode.value) {
// GO RIGHT
// Check if the right side of the current node is empty
if (!currentNode.right) {
currentNode.right = newNode;
return this;
}
// if it's not empty
// update the current node
currentNode = currentNode.right;
}
}
}
}
lookup(value) {
const newNode = new Node(value);
// check if root node doesn't exists
if (!this.root) {
return false;
}
let currentNode = this.root;
if (currentNode.value === newNode.value) {
console.log("Node found!");
return currentNode;
}
while (currentNode) {
if (currentNode.value > newNode.value) {
if (currentNode.left.value === newNode.value) {
console.log("Node was found on left wing");
return currentNode.left;
}
currentNode = currentNode.left;
} else if (currentNode.value < newNode.value) {
if (currentNode.right.value === newNode.value) {
console.log("Node was found on right wing");
return currentNode.right;
}
currentNode = currentNode.right;
} else {
return "Node not found";
}
}
}
}
// 9
// 4 20
// 1 6 15 170
const tree = new BinarySearchTree();
tree.insert(9);
tree.insert(4);
tree.insert(20);
tree.insert(1);
tree.insert(6);
tree.insert(15);
tree.insert(170);
console.log(tree.lookup(20));
Congratulations 🎉🎉!
You've successfully built your own Binary Search Tree. I hope this hands-on experience has deepened your understanding of tree data structures. Keep exploring and experimenting with code. Happy coding!"
Subscribe to my newsletter
Read articles from Ayoola Adewale directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Ayoola Adewale
Ayoola Adewale
Hi, My name is Ayoola. I'm thejuggernaut, here to put a dent in the universe. I'm a software developer with about 4 years of experience building and maintaining web/mobile applications