chicken swarm optimization algorithm

The Chicken Swarm Optimization algorithm is a nature-inspired optimization technique that mimics the behavior of chickens in a flock. This algorithm is designed to solve abstract non-deterministic problems through the process of simulating the behavior of chickens in a flock where the chickens follow the lead of a rooster to find an optimal solution for the problem at hand.

Introduction

Free Vector | Black rooster realistic side view image

This algorithm is a meta-heuristic algorithm used to solve complicated optimization problems through the process of mimicking the behavior of chickens in a flock. The algorithm begins by initializing a population of chickens where every chicken represents a potential solution to the optimization problem and the population is divided into 3 groups based on their levels of fitness - Roosters, Hens, and Chicks. Roosters are the best-fit solutions, hens are less fit but still viable solutions and chicks are the least fit solutions.

The algorithm has been shown to perform well across various optimization problems, demonstrating its effectiveness in terms of both optimization accuracy and robustness. Experiments on benchmark problems have shown that the algorithm can achieve good results, outperforming other algorithms in some cases.

Inspiration

The chicken swarm optimization algorithm is inspired by the hierarchical behavior and social intelligence observed in chicken swarms. This algorithm aims to harness the swarm intelligence behavior exhibited by a flock of chickens to solve complicated optimization problems. The inspiration behind this algorithm is rooted in the intricate social structure of chicken swarms, where roosters, hens, and chicks tend to exhibit distinct behaviors that contribute to the swarm's overall efficiency and adaptability.

In a chicken swarm, roosters are the leaders, guiding the flock toward food sources and safety. Hens follow the roosters, often staying closer to them, while chicks are the youngest and least experienced members of the swarm. They are responsible for exploring the surroundings and bringing back information to the rest of the flock. This hierarchical structure, where each member plays a specific role, is a key aspect of the swarm's intelligence and adaptability/

The algorithm's design is informed by the chicken swarm's ability to adapt to changing conditions, such as predators or changing food sources, by adjusting their behavior based on the collective intelligence of the swarm. This adaptability is a key feature of the algorithm, as it allows the algorithm to dynamically adjust its search strategy to find the optimal solution more efficiently.

In summary, the inspiration behind the Chicken Swarm Optimization algorithm lies in the social and hierarchical intelligence observed in chicken swarms. By mimicking this behavior, the algorithm aims to efficiently solve complex optimization problems by leveraging the collective intelligence of the swarm.

Convergence

The convergence of this algorithm is considered to be one of the key aspects for determining its performance and benchmarking how well the algorithm can find an optimal solution for the problem in hand within a set number of iterations. The convergence refers to the process where the algorithm settles on a solution that is close to the optimal one, often after a significant number of iterations.

The convergence of this algorithm is influenced by several factors, including the initial population distribution, the selection process of roosters and chicks, and the search strategies employed by the algorithm. The algorithm's convergence properties have been extensively studied with research focusing on understanding and improving the algorithm's efficiency in finding optimal solutions for the problem at hand.

The convergence of this algorithm like the other meta-heuristic algorithms is dependent on the balance between the exploration and exploitation process depicted by it. The algorithm in general tends to dynamically adjust its search strategies to ensure that the population is able to explore the search space effectively while also exploiting the best solutions found so far and this balance proves to be critical for the algorithm's ability to converge to high-quality solutions.

Exploration vs Exploitation in the Chicken Swarm Optimization Algorithm

The balance between exploration and exploitation is a fundamental aspect of the chicken swarm optimization algorithm. This balance is crucial for the algorithm's ability to traverse and navigate through an existing search space to efficiently find a solution for the optimization problem at hand.

The exploration process refers to the searching of the solution space for a new potentially better solution and in this algorithm, this process is primarily handled by chicks who are responsible for exploring the search space and bringing back potential solutions for evaluation. The exploration strategies employed by chicks, such as simultaneous search and spiral search, are designed to encourage them to discover new areas of the search space that have not been thoroughly explored yet. This aspect of the algorithm mimics the behavior of chicks in a chicken swarm, where they are responsible for exploring the environment and gathering information about potential food sources or threats.

Exploitation, on the other hand, works on the rule of making the best use of the optimal solutions discovered so far to guide the search process towards these solutions. This task is mainly carried out by the roosters, who are the best solutions found within the population. The roosters guide the search process by moving towards the best solutions, encouraging the chicks to follow them and this behavior is inspired by the leadership role of roosters in chicken swarms, where they guide the flock towards the best potential food sources in real life.

Algorithm

The chicken swarm optimization algorithm is a bio-inspired optimization algorithm that draws its inspiration from the hierarchical and social behaviors exhibited by chicken swarms. The algorithm begins by initializing a population of chickens, each representing a potential solution to the optimization problem at hand. In this algorithm, the population is divided into 3 groups based on their fitness: Roosters, Hens, and Chicks. Roosters are the best solutions found so far, guiding the flock towards the optimal solution. Hens, being less fit but still capable of finding solutions, follow the roosters and help maintain the flock's cohesion. Chicks, the least fit, are responsible for exploring the search space and bringing back solutions for the hens and roosters to evaluate.

After this, the algorithm proceeds with a series of steps to find more optimal solutions:

New Population Distribution: The algorithm calculates the new positions for the roosters and chicks. The rooters' positions are updated based on the best solution found so far, and the chicks' positions are updated based on the roosters' positions and a random factor.
Best Guided Search for Roosters: The roosters are guided towards the best solution found so far and this is achieved by updating the positions of the roosters' based on the difference between the best solution and the current best solutions along with a random factor.
Simultaneous and Spiral Search for Chicks: The chicks perform simultaneous and spiral searches to explore the search space more effectively. This involves updating the chicks' positions based on the roosters' positions and incorporating a random factor, simulating the behavior of chicks following the lead of the roosters.

The Search Strategies Followed in this Algorithm

Now, let's take a step back to analyze and understand the cryptic method through which the chicks look for solutions for the optimization problem in hand. The chicks in general tend to follow any of the 2 methods for the search process: Simultaneous Search and Spiral Search.

Simultaneous Search: In this search strategy, all the chicks move toward the roosters' positions simultaneously. This approach is inspired by the behavior of chicks that follow the lead of the roosters, moving towards the best solution found so far. The simultaneous search allows the chicks to quickly converge on the promising areas of the search space, , thereby increasing the chances of finding the optimal solution. However, this strategy can lead to a high degree of synchronization, which might limit the diversity of exploration.
Spiral Search: In this search strategy, the chicks move in a spiral pattern around the roosters. This movement is designed to encourage the chicks to explore the search space more thoroughly, covering areas that might not be reached during a simple simultaneous search. The spiral search is particularly effective in problems where the optimal solution is not located in the immediate vicinity of the current best solutions. By spiraling outwards, chicks can explore the search space more effectively, potentially discovering new and better solutions.

The choice between simultaneous and spiral search strategies can significantly impact the performance of the chicken swarm algorithm. Simultaneous search is generally faster and can be more efficient in problems where the optimal solution is nearby. However, in problems with a large search space or where the optimal solution is not easily accessible, the spiral search strategy can be more effective. The algorithm typically alternates between these strategies, using simultaneous search to quickly converge on promising areas and spiral search to explore the search space more thoroughly.

Search Parameters used by the Chicken Swarm Optimization Algorithm

The chicken swarm optimization algorithm uses the following parameters in general -

Population Size: The number of solutions [chickens] in the population influences the diversity of the search and the algorithm's ability to explore the search space and a larger population size can lead to higher exploration but this can increase the amount of computing resources required.
Learning Rate: This parameter controls how much the solutions (chickens) adjust their positions based on the roosters' positions and the search strategy (simultaneous or spiral search). A higher learning rate allows for faster convergence but may also lead to premature convergence to suboptimal solutions.
Spiral Learning Rate: Specific to the spiral search strategy, this parameter controls the extent to which the chicks spiral outwards in the search space. It influences the balance between exploration and exploitation, with a higher rate leading to more extensive exploration but potentially at the expense of exploiting the best solutions found so far.
Random Factor: To introduce randomness in the search process and prevent the algorithm from getting stuck in local optima, a random factor is used. This factor influences the direction and extent of the chicks' movements, ensuring that the search does not become deterministic.
Selection Pressure: This parameter influences how much the algorithm favors the best solutions (roosters) over the less fit solutions (hens and chicks). A higher selection pressure means that the algorithm will more strongly favor the roosters, potentially accelerating the convergence to the optimal solution.
Elitism: This parameter controls the proportion of the best solutions (roosters) that are preserved across generations. Elitism ensures that the algorithm does not lose the best solutions found so far, which can be crucial for maintaining the quality of the search.

Variations of the Chicken Swarm Optimization Algorithm

The chicken swarm optimization algorithm has had variants developed on top of it to enhance the algorithm's performance, efficiency, and applicability to various optimization problems, some of these variants are :

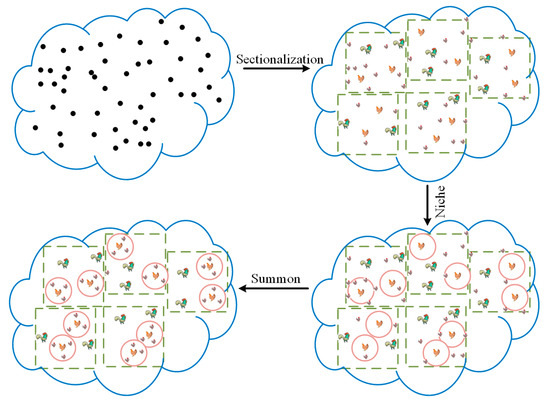
Performance-Enhanced Chicken Swarm Optimization: This variant includes performance-enhancing strategies to improve the computational efficiency and solution quality of the chicken swarm optimization algorithm. These enhancements include mechanisms for the free grouping of populations, synchronous updating of individuals within niches, and the spiral learning of chicks. The goal of this algorithm is to balance exploitation and exploration more effectively in this algorithm leading to more effective and efficient search strategies and faster convergence.
Improved Chicken Swarm Optimization Algorithm for MultiModal Problems: This variant aims to enhance the original algorithm by refining its search strategies and parameters and also includes variations to the search algorithms used by the individual roosters and chicks thus introducing new mechanisms for exploration ad exploitation and optimization convergence in the algorithm.
Adaptive Chicken Swarm Optimization: This variant focuses on making the algorithm more adaptive to the characteristics of the optimization problem at hand. It might involve adaptive selection pressures, learning rates, and search strategies that can be adjusted based on the problem's characteristics. The goal of this variant is to ensure that the algorithm can effectively explore the search space and converge to optimal solutions for a wide range of optimization problems.
Robust Chicken Swarm Optimization: This variant aims to enhance the robustness of the algorithm by incorporating mechanisms that make it more resilient to changes in the problem environment of the parameters. This could include strategies for handling noise in the data, adapting to changes in the search space, or improving the algorithm's ability to recover from unfeasible solutions.

Overall, these variants include specific types of enhancements aimed at addressing very particular challenges of limitations of the original algorithm if any to solve the problem at hand making it more effective and versatile in nature.

Applications of the Chicken Swarm Optimization Algorithm

This algorithm can be used in a wide amount of domains some of which are:

Engineering Design: The algorithm's ability to efficiently extract and apply swarm intelligence makes it suitable for engineering design optimization problems. It can be used to optimize the design of various engineering systems, including mechanical, electrical, and civil engineering systems by searching for the most optimal designs meeting the specific constraints set.
Structural Optimization: This algorithm can be used to optimize the structural design of buildings, bridges, and other infrastructure to meet specific performance criteria, such as strength, durability, and cost-effectiveness.
Production and Manufacturing: In production and manufacturing processes, the algorithm can be used to optimize the production schedule, resource allocation, and material selection to improve efficiency and reduce costs. This can include optimizing the production of goods, components, or services.
Logistics and Supply Chain Management: The algorithm can be applied to optimize logistics and supply chain management processes. This includes optimizing routes, schedules, and inventory levels to improve the efficiency of transportation, warehousing, and distribution networks.
Environmental and Ecological Optimization: Given its ability to efficiently explore the solution space, the algorithm can also be applied to environmental and ecological optimization problems. This can include optimizing the allocation of resources in nature conservation, optimizing the use of renewable energy sources, or optimizing the management of ecological systems.

In summary, the Chicken Swarm Optimization algorithm, inspired by the hierarchical order and behaviors of chicken swarms, has shown promise in solving a wide range of optimization problems across various domains. Its ability to efficiently extract and apply swarm intelligence makes it a versatile tool for optimization applications, from engineering design to environmental and economic modeling.

Limitations of the Chicken Swarm Optimization Algorithm

The limitations of this algorithm include -

Computational Complexity: The algorithm in its early stages can prove to be computationally intensive because of the need to maintain and update the positions of all chickens and roosters in the swarm, leading to high amounts of computational costs for large-scale optimization problems.
Local Optima: The algorithm can get stuck in local optima, where the algorithm converges to a solution that is best within a local neighborhood of the search space but not necessarily the global optimum. This limitation is particularly pronounced in problems with multiple local optima or in problems where the global optimum is significantly different from the local optima.
Parameter Sensitivity: The performance of this algorithm can be highly sensitive to the choice of parameters used like the population size, learning rate, and the balance between exploration and exploitation.
Convergence Rate: The rate at which the algorithm converges to an optimal solution can vary depending on the characteristics of the problem and the algorithm's parameters. In some cases, the algorithm may converge slowly, especially in problems with a large search space or where the optimal solution is difficult to reach.
Adaptability to Non-Continuous Problems: While this algorithm can be adapted to solve discrete optimization problems, its strength lies in solving continuous optimization problems. The algorithm's ability to adapt to solve the problem in hand might not prove to be as accurate especially when it has to work effectively for a problem with discrete variables or with set constraints.
Lack of Robustness to Noise: This algorithm may not perform well in noisy environments or environments with high amounts of uncertainty. The algorithm's performance can be negatively impacted by the noisy data or uncertainty in the objective function, making it challenging to find the optimal solution in such scenarios.

In summary, while the Chicken Swarm Optimization algorithm offers a novel and effective approach to solving optimization problems, it shares common challenges with other optimization algorithms, including computational complexity, sensitivity to parameter choices, and difficulties in handling certain types of problems or environments. Researchers and practitioners often need to address these limitations through algorithmic modifications, parameter tuning, and the application of additional techniques to enhance the algorithm's performance.

Code Implementation with Python

The algorithm can be implemented programmatically using Python like so -

import numpy as np

def cso(func, lb, ub, n_chicken, max_iter):
  """
  Implements the Chicken Swarm Optimization (CSO) algorithm.
  It returns a tuple containing the best position and the best fitness value.
  """

  # Initialize positions and fitness values
  positions = np.random.uniform(lb, ub, size=(n_chicken, len(lb)))
  fitness = np.array([func(p) for p in positions])
  best_position = positions[np.argmin(fitness)]
  best_fitness = np.min(fitness)

  # Chicken swarm optimization loop
  for _ in range(max_iter):

    # Update positions based on social and foraging behavior
    for i in range(n_chicken):
      # Social behavior (following the rooster)
      if fitness[i] > fitness[np.argmin(fitness)]:
        sigma = np.random.uniform(0, 1)
        positions[i] = sigma * positions[i] + (1 - sigma) * best_position

      # Foraging behavior (random exploration)
      levy_steps = np.random.normal(scale=0.01, size=positions[i].shape)
      levy_steps *= np.power(np.fabs(levy_steps), 1/3)
      positions[i] += levy_steps

      # Clip positions to the search space
      positions[i] = np.clip(positions[i], lb, ub)

    # Update fitness values
    fitness = np.array([func(p) for p in positions])

    # Update best position and fitness
    if np.min(fitness) < best_fitness:
      best_position = positions[np.argmin(fitness)]
      best_fitness = np.min(fitness)

  return best_position, best_fitness

# Example usage 
def objective_function(x):
  return np.sum(x**2)

# Define search space bounds
lb = np.array([-10, -10])
ub = np.array([10, 10])

# Run the algorithm
best_position, best_fitness = cso(objective_function, lb, ub, 50, 100)

print("Best position:", best_position)
print("Best fitness:", best_fitness)

The Python code above implements the Chicken Swarm Optimization algorithm. It simulates a flock of chickens searching for food. Chickens follow the fittest "rooster" (social behavior) while also exploring randomly (foraging behavior). This loop continues for a set number of iterations. The code keeps track of the best position (food source) found by any chicken throughout the search. Finally, it returns the location of the best food source and its quality.

Conclusion

In conclusion, this algorithm inspired by the social and hierarchical behaviours of chicken swarms, has emerged as a promising approach to solving complex optimization problems. Its design, which mimics the roles of roosters, hens, and chicks within a chicken flock, allows for the efficient exploration and exploitation of the solution space, ensuring a balance between these two critical aspects of optimization.

The ability of the algorithm to adapt to the characteristics of the optimization problem at hand, through the implementation of performance-enhanced strategies such as free grouping of populations, synchronous updating of individuals within niches, and spiral learning of chicks, has been demonstrated to significantly enhance its computational efficiency and solution quality. These improvements not only contribute to the algorithm's effectiveness in solving optimization problems across various dimensions but also ensure its robustness against local optima, making it a versatile tool for a wide range of applications.

Moreover, the experimental results highlight the algorithm's superior performance in handling unimodal and multimodal functions, as well as its effectiveness in jumping out of local optima, especially in higher dimensions. This is attributed to the algorithm's ability to balance exploration and exploitation effectively, which is crucial for navigating the complex landscape of optimization problems.

Despite its strengths, it also faces challenges, including computational complexity and sensitivity to parameter choices. However, these limitations can be mitigated through careful algorithmic design and parameter tuning, ensuring the algorithm's applicability across a broad spectrum of optimization problems.

In the future, further research into the algorithm and its variants is heavily encouraged, with a focus on exploring novel mechanisms for enhancing the algorithm's exploration and exploitation capabilities, as well as improving its robustness and adaptability to different optimization scenarios. The ongoing development of the algorithm and its applications represent a significant step forward in the field of optimization, paving the way for more efficient and effective solutions to complex problems.

Swarm Intelligence Series : Chicken Swarm Optimization Algorithm

Table of contents