Swarm Intelligence Series: Particle Swarm Optimization Algorithm

Let's kick off the series of swarm intelligence algorithms using the Particle Swarm Optimization algorithm. This algorithm is a computational method used to optimize and solve a problem by iteratively improving upon an identified candidate solution in a step-by-step manner based on a given measure of quality.

Introduction

Imagine a flock of birds effortlessly navigating the vast sky, where their movements seem coordinated perfectly by the will of nature. This collective intelligence where individuals in a group or swarm learn and adapt based on the collective experiences of the group has culminated in the foundation of the PSO algorithm, a powerful optimization technique to solve optimization problems.

The PSO Algorithm is a population-based search algorithm that mimics the social behavior of bird blocking. It was first introduced by Kennedy, and Eberhart in 1995. In PSO, a swarm of particles tends to "fly" or move around a search space where every single one of them represents a potential solution to solve the problem at hand and each particle has a position and a velocity, which are updated based on its present position (pbest) and the best position of its neighbors (gbest).

It operates by having a population of candidate solutions, known as particles that move around in random order through the search space according to a fixed set of mathematical formulas, and each particle's movement is influenced by its own best-known position and the best-known positions of the entire swarm, which are updated as the better positions discovered by the other particles. This process is expected to guide the swarm towards the best solutions.

Inspiration behind the PSO Algorithm

The original goal of the PSO algorithm was to simulate the graceful but unpredictable choreography of a bird block. In nature, the observable vicinity of any bird is limited to only a certain range. However, if there is more than one bird, this will allow all of the birds in the swarm to be aware of a larger surface of a fitness function. This concept was mathematically modeled to guide the swarm towards finding the global minimum of a fitness function, which is the objective of optimization problems, and the collective behaviors of these groups or "swarms" led to the inspiration for the development of the PSO Algorithm.

Biological swarming behaviors like flocking and schooling are characterized by the ability of the individuals in the search space to coordinate their movements in such a way that it benefits the swarm as a whole. For example, birds in a flock will adjust their flight paths to avoid collisions, maintain the flock's cohesion, and find food efficiently. Similarly, the fishes in a school move in a coordinated pattern to find food and safeguard themselves from potential dangers like predators and so on. These behaviors are the result of a simple set of pre-determined or set rules or consensus between these individuals in the wildlife leading to complex, emergent, and repetitive behavior that proves to be beneficial for them.

The adaptability and learning capabilities displayed by these flocks of animals also proved to be crucial for the development of these ML algorithms. The ability of the swarm to learn from its environment make adjustments to its behaviors and basically "course-correct" itself depending on the situation in its surroundings, proved to form one of the core aspects of this algorithm and this also helped to improve and refine the solution finding process to solve the optimization problem the algorithm is being used against. This learning process is iterative with each particle participating in the algorithm within the current search space continually improving and changing their direction to get a much more refined solution. At its best, the swarm which is a part of the current PSO iteration tends to learn from the fitness of the solutions it explores, and adjusts its velocity and position of the particle to guide them towards better solutions.

Capabilities of the virtual agents participating in the PSO Algorithm

In the realm of the PSO Algorithm, a captivating journey has been envisioned in the realm of wildlife with birds and fishes flocking together to solve a common problem, and has been modeled in computer science in the form of bits instead. In the case of the PSO Algorithm, we have particles that form the "flock" of the algorithm which embark on a quest through the digital landscape to identify optimal solutions for the problem in hand to the best of the model's ability.

These particles also called "AI Agents" navigate the vast search space with a sense of curiosity and purpose, embodying unique capabilities or characteristics that will set them apart from their real-world wildlife counterparts. These virtual agents unlike their wildlife counterparts however possess special properties to them and have unique abilities which are :

1. Memory: Imagine each particle to possess memory akin to an AI model's recollection of the past training data that led to its peak performance. This "personal best" (pbest) serves as a beacon guiding the particles back to regions of promise, much like how a seasoned chess player draws upon successful strategies from memory.

2. Social Learning: Similar to how groups of fishes or birds pick up and learn collectively by sensing social cues, the particles participating in the search process delve into the realm of collaborative learning where the particles glean insights from their peers. The swarm as a whole of these particles collectively uses all of the ideas gathered by the individual particles to track the best globally optimum solution to solve the problem at hand which has been discovered so far that act like a shared target for the particles to hit and beat which then will get updated again thus improving the performance or efficiency of solving the task in hand.

3. Adaptability: The concept of momentum within each particle influences its exploration strategy and the higher the momentum levels, the more broader searches can occur across the search space giving us a bigger set of globally optimum solutions. Conversely, lower momentum values of the particles are used for fine-tuning purposes and for refinement near the optimum solutions mirroing an AI model adjusting its learning rate based on a problem's complexity like a vehicle modifying its speed based on the terrain conditions it is being driven on.

Algorithm for the PSO

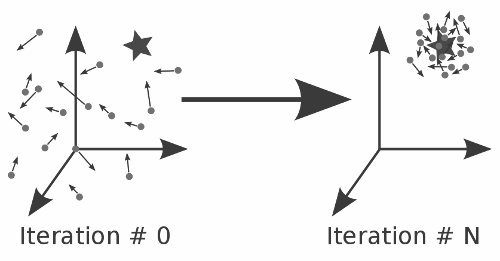
Particle Swarm Optimization (PSO) is a metaheuristic optimization algorithm inspired by the social behavior of bird flocking or fish schooling. It aims to find the optimal solution to a problem by iteratively improving a candidate solution based on a given measure of quality. Here is a clear, step-by-step algorithm for PSO:

Initialization

1. Particle Initialization: Initialize a population of particles, each representing a potential solution to the problem. Each particle has two main attributes: position and velocity. The position is a vector representing the coordinates of the solution in the search space, and the velocity is a vector representing the direction and speed at which the particle will move. Both the position and velocity are typically initialized randomly within the bounds of the problem.

2. Best Known Positions: For each particle, initialize the best-known position (pbest) and the best-known fitness (fbest) to the particle's initial position and the fitness of that position. The fitness is a measure of how good the solution is, determined by a fitness function specific to the problem.

3. Swarm Best Known Position: Initialize the swarm's best-known position (gbest) to the position of the particle with the best fitness among all particles.

Iteration

For each iteration of the algorithm, perform the following steps:

1. Fitness Evaluation: Evaluate the fitness of each particle's current position using the fitness function.

2. Update Best Known Positions: If a particle finds a better solution (i.e., a position with a better fitness), update its best-known position and best-known fitness. Also, if the swarm's best-known position is updated, update the swarm's best-known position.

3. Update Velocity: For each particle, update its velocity based on its own best-known position, the swarm's best-known position, and the current velocity. This is typically done using a combination of the current velocity, the difference between the particle's current position and its best-known position, and the difference between the swarm's best-known position and the particle's current position.

4. Update Position: For each particle, update its position by adding the updated velocity to the current position.

5. Termination: If a termination criterion is met (e.g., a maximum number of iterations is reached, or the solution quality is satisfactory), stop the algorithm. Otherwise, go back to the fitness evaluation step for the next iteration.

Convergence in the PSO, What it means?

The Convergence to a local optimum has been the main problem that is to be solved using the PSO algorithm. While it has been proven that the PSO needs modifications to guarantee finding a local optimum, the convergence capabilities of different PSO algorithms and parameters depend on the empirical results. A lot of strategies have been proposed to improve the performance of the PSO algorithm including the development of an "orthogonal learning" strategy which aims to improve the convergence speed and solution quality.

Variants of the PSO Algorithm

There are numerous variants of the basic PSO Algorithm that have already been developed to cater to the needs of the specific kinds of optimization problems that are to be solved. These variants include the different ways to initialize the particles and their velocities, how to dampen the velocity, and whether to update the best-known positions only after the entire swarm has been updated.

1. Variations in Initialization: One of the key areas where these variants differ is in how the particles and velocities have been initialized and utilized to solve the problem at hand. Traditional PSO begins with the random initialization of both the position and velocity for every particle. However, some variants introduce more sophisticated initialization strategies. For example, the initialization-free PSO IFPSO does not require any initial values for the positions and velocities of the particles to solve for the optimum solution but it instead uses a mathematical function to determine their initial positions based on the problem's characteristics. This approach can lead to faster convergence and better exploration of the search space.

2. Variation through the process of Dampening the Velocity: Another area of variation in the parameters of the PSO algorithm is called "Dampening Velocity". In the original PSO algorithm, the velocity is updated based on the particle's own best position and the swarm's best position, with a constant inertia weight. Variants like Cognitive PSO (CPSO) and Social PSO (SPSO) introduce modifications to the velocity update rule, such as using a linearly decreasing inertia weight to encourage the exploration in the early stages of the algorithm and exploitation in later stages. This inertia weight is used to encourage exploration in the early stages of the algorithm and exploitation in later stages. This dynamic adjustment of the inertia weight can help to avoid premature convergence to suboptimal solutions.

3. Variations in timing the best position updates: The timing of the updating of the best-known positions is another critical area of variation. In the original PSO, each particle updates its best position whenever it finds a better solution, and the swarm's best position is updated whenever any particle finds a better solution. Some variants, such as Adaptive PSO (APSO), introduce a more nuanced rule for updating these best positions. For instance, APSO uses a scale-adaptive fitness evaluation mechanism that allows for the algorithm to adjust its fitness evaluation based on the current progress of the optimization, which can lead to an increase in the convergence speed and solution quality.

The Process of Exploration and Exploitation in the PSO Algorithm

The PSO algorithm simulates the social behavior witnessed in wildlife to achieve the goal of solving an optimization problem by optimizing some objective function in a step-by-step or iterative fashion through the modification of the current best position and updating it to find the best optimal solution possible to solve the task at hand.

It employs exploration and exploitation to do all of these steps and to reach the maxima or minima at the end as required by the problem at hand and does this all iteratively.

• Exploration

Exploration in the PSO Algorithm refers to the ability of the algorithm to search for new solutions to search for new solutions beyond those that have been already discovered. It encourages the particles to move away from previously visited areas to avoid getting trapped in the local minima. Excessive exploration however could lead the algorithm astray and slow down the progress of solving the problem because the particles may end up spending too much time exploring unpromising regions without focusing enough on the promising ones. However, insufficient exploration will result in a higher chance of reaching a sub-optimal solution and therefore a premature convergence can occur.

In the PSO Algorithm, exploration is achieved through the cognitive and social components of velocity update equations, these components tend to encourage the particles to move towards new positions based on their current personal best achieved and the global best positions. As long as these components are not zeroed out in nature, the particles in the search space tend to explore and continue their search.

• Exploitation

On the other hand, exploitation in the PSO Algorithm refers to the process of the algorithm to improve upon the currently discovered pieces of solution in a step-by-step manner. Once a good solution has been identified, exploration ensures that the algorithm continues to fine-tune it until no further improvements can be made. Too little exploitation results in the poor utilization of the available information and resources as well that have been gathered during the initial exploration process, leading to wasted computation effort. Conversely, excessive amount of exploitation could lead the algorithm to become stagnant and converge just to the current sub-optimal maxima or minima while solving for the optimization problem making the algorithm's solution pre-mature and inefficient and thereby this stops the algorithm from exploring more making it unproductive and ignorant.

In PSO, exploitation occurs when the particles converge towards their personal best and global best positions. When a particle finds a better solution than its previous best, it updates its personal best as required and similarly if another particle in the search space that is participating discovers an even better solution that beats the global best, all of the particles update their velocities and positions according to this new global optimum solution. Thus, the exploitation is generally a natural step due to the iterative nature of the PSO algorithm.

To summarize, it is crucial to maintain a good enough balance between both of these processes in the PSO algorithm while solving an optimization problem to ensure its success. while exploration enables for the discovery of potential novel solutions, exploitation is used to improve upon them. Achieving this balance requires careful tuning of various algorithmic parameters like the inertia weight, cognitive and social coefficients, and the maximum velocity limits.

Search Parameters used for the PSO Algorithm

The PSO Algorithm includes some tuning parameters which are utilized as conditionals for how it picks out optimal solutions in each step and can also act as conditions required to stop the algorithm. These parameters are mainly used as constraints for the search process and also act as a guide for the algorithm to undertake the search process while balancing both exploration and exploitation. Some of the key parameters heavily used in general for the PSO Algorithm are :

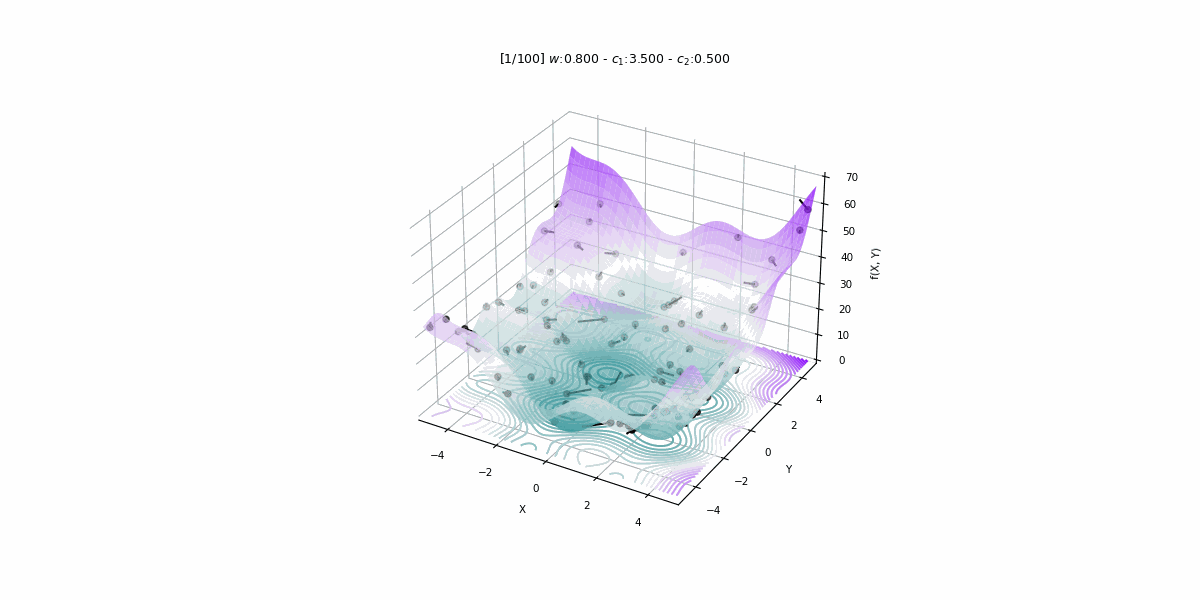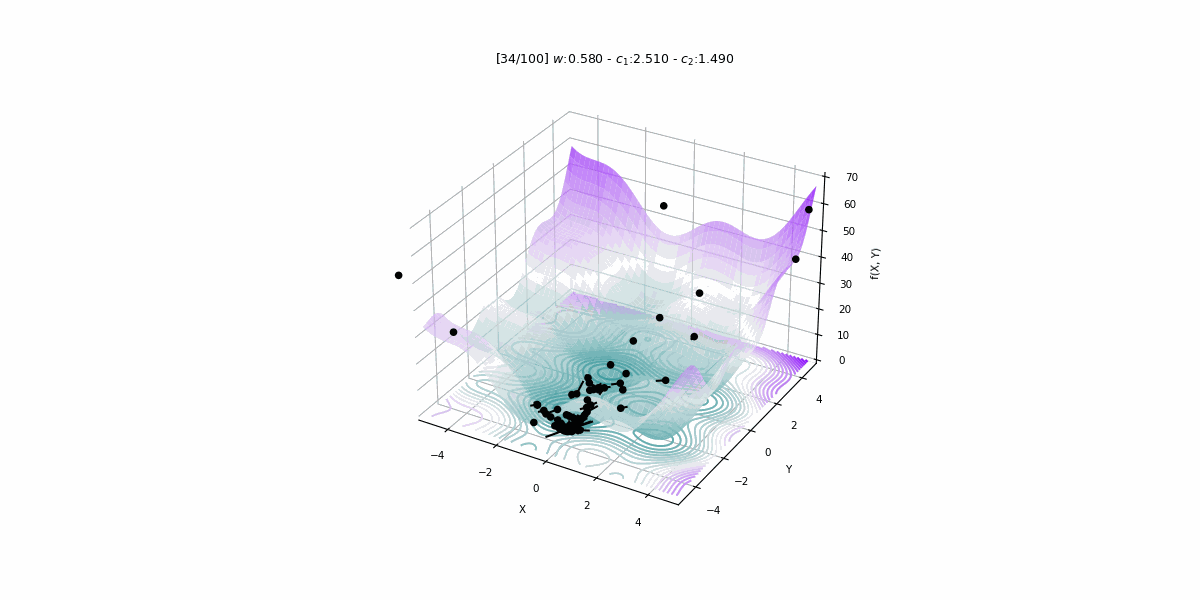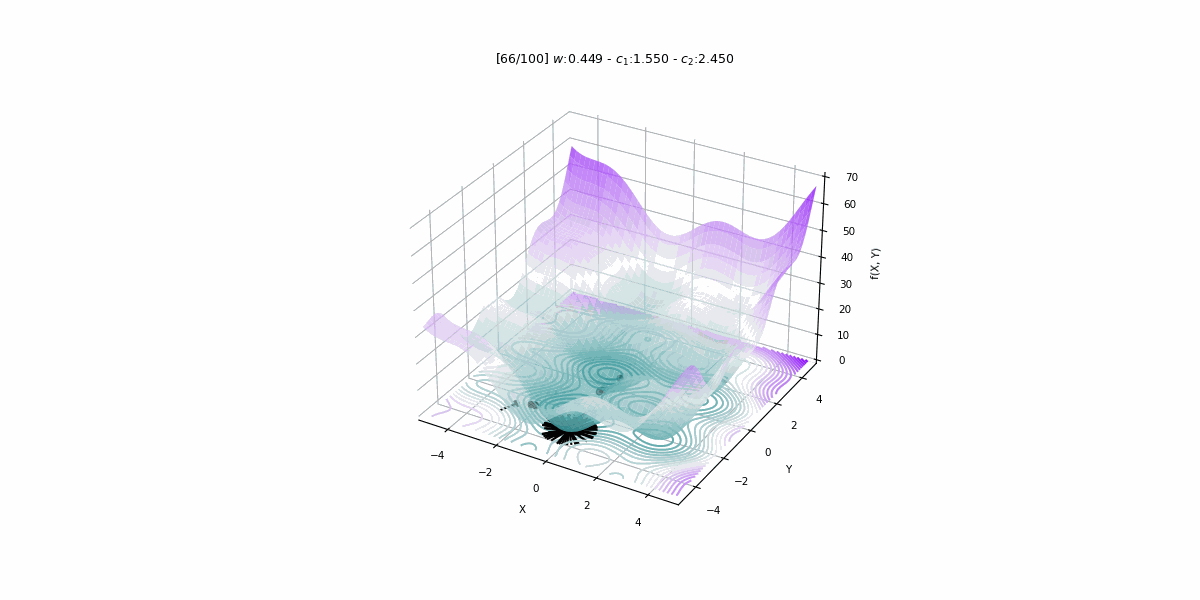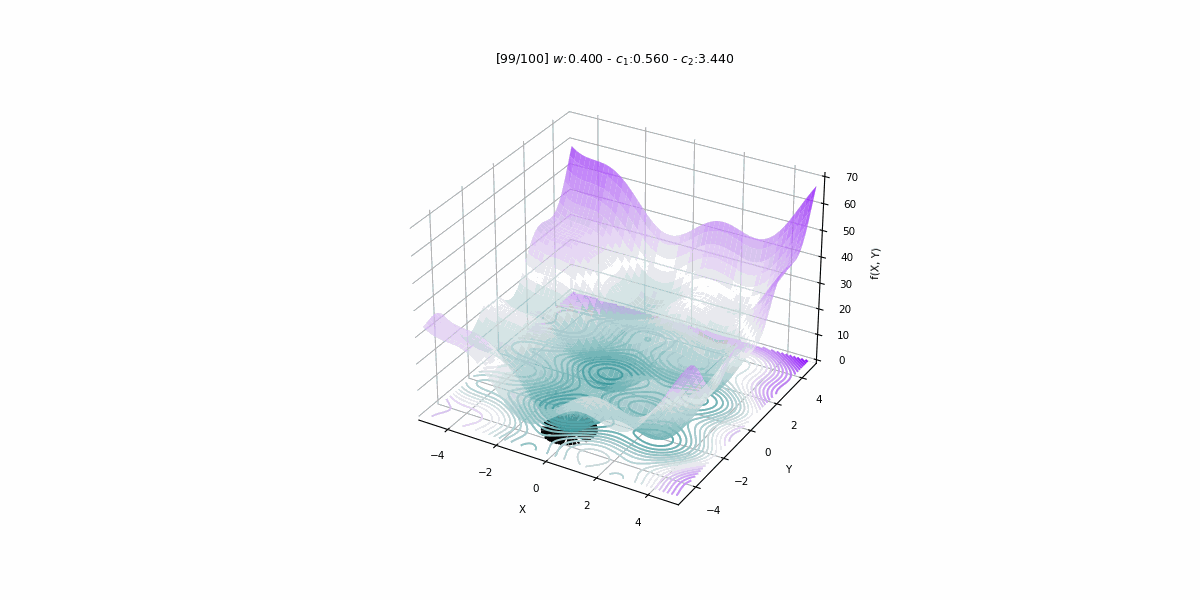
1. Inertia Weight (w): This controls the amount of momentum that is carried forward from the previous step. High inertia weight promotes exploration while low values tend to favor exploitation and a typical range is between 0.1-0.9 in range in general with a decay schedule often employed to ensure convergence.

2. Cognitive Coefficient (c1): This parameter determines the relative importance between a particle's own best position versus the global best position. Higher values promote exploration while lower values tend to focus more on exploitation and the common range for this is between 1-3.

3. Social Coefficient (c2): The social coefficient is another parameter that is similar to the cognitive coefficient parameter which is utilized to regulate the influence of the globally optimum solution on every particle. Higher values of the social coefficient promote exploration whereas lower values promote exploitation instead and its ranges are between 1-3. The reason for the value of the social coefficient switching between exploration and exploitation is that when it is at a high value, the algorithm is more in an exploration state where it amplifies the impact of the globally optimum solution on the individual particle's movement which incentivizes the particles in the search space to explore more and more regions. Whereas, a lower value of the social coefficient will reduce the importance of the global optimum and the particles will now tend to focus more on exploiting the currently known best regions and will not explore new search spaces that have been previously unexplored.

4. Maximum Velocity (Vmax): This parameter is used to prevent the particles from traveling excessively far in a single step and it ensures that bounds or boundaries are set for every particle reasonably without it going off exploring on its own to an unproductive spot in the search space and this value typically tends to scale with the problem dimensions and may decrease over time to allow deeper exploration early on in the search process.

5. Acceleration Constraints / Constants (1c and 2c): The acceleration constants mainly improve and scale the cognitive and social components of the velocity update equation respectively. When its value is greater than 1, it amplifies the corresponding effects of acceleration or velocity on the particles and when the value is less than 1, it leads to "dampening" of the velocity. Typical values for acceleration constants lie between 1-3.

6. Number of Particles (m): This parameter sets the size of the swarm. Smaller swarms generally tend to converge much quicker but larger swarms offer increased coverage of the search space. Typical sizes of the number of particles in a swarm lie between 20-100 however this is heavily influenced by the complexity and specifics of the problem to be solved or searched upon.

7. Max Iterations (Tmax): This parameter specifies the termination criterion for the algorithm. If the swarm fails to achieve satisfactory results after reaching this limit, the algorithm halts.

Overall, the inertia weight and both the cognitive coefficient variables act as the main parameters responsible for improving the speed, convergence, and rate of learning for the PSO algorithm and they are the critical parameters controlling the overall performance and ability of it to solve the given problem.

Simplifications of the PSO Algorithm

Some of the notable simplifications of the PSO Algorithm that aim to reduce its complexity without compromising performance are -

1. Barebones PSO: This version of the PSO Algorithm eliminates the velocity component replacing it with direct, straight-forward updates to the position. While this reduces complexity, it can compromise performance due to the absence of the guidance given by the velocity.

2. Accelerated PSO: Similar to the barebones PSO, accelerated PSO also ignores the velocity component used for guidance but it maintains a simplified update rule that can improve the convergence rate in various applications.

Code implementation with MealPy

We will be utilizing the MealPY library for the hyperparameter tuning of a random objective function and applying the PSO Search Algorithm to find the optimal solution.

import numpy as np
from mealpy import FloatVar, ABC

def objective_function(solution):
    return np.sum(solution**2)

problem_dict = {
    "bounds": FloatVar(lb=(-10.,) * 30, ub=(10.,) * 30, name="delta"),
    "minmax": "min",
    "obj_func": objective_function
}

model = ABC.OriginalABC(epoch=1000, pop_size=50, n_limits = 50)
g_best = model.solve(problem_dict)
print(f"Solution: {g_best.solution}, Fitness: {g_best.target.fitness}")

The ABC function provides access to the PSO Algorithm which is run over here for over 1000 epochs to find an optimal solution.

Applications of the PSO Algorithm

PSO has found wide application in various fields, including machine learning, control systems, engineering, and financial modeling. Its ability to search very large spaces of candidate solutions and its adaptability to different problem characteristics make it a popular choice for solving complex optimization problems as it doesn't require a lot of complex and specific information about the problem to be solved. Some of its applications are :

1. Hyperparameter Tuning: The PSO algorithm is heavily used for the process of hyperparameter tuning and is used to modify and optimize the learning rates, hidden layer sizes, and activation functions to improve the performance of the model.

2. Feature Selection: The PSO Algorithm can help you identify the most relevant features of your data improving the accuracy and efficiency of your machine learning models.

3. Ensemble Learning: PSO can be used to create diverse and effective ensembles of machine learning models, boosting their overall performance. Imagine it as training a team of AI specialists, each with unique strengths, to tackle a complex problem from different angles. This diversity leads to more robust and accurate solutions.

4. Reinforcement Learning: PSO can be incorporated into reinforcement learning algorithms, helping agents explore and learn optimal policies in complex environments. Think of it as guiding a virtual AI robot through a maze, using both individual exploration and observing the successes of others to navigate efficiently.

Conclusion

Particle Swarm Optimization is a powerful and versatile optimization algorithm that has found widespread application in numerous fields. Its simplicity, adaptability, and effectiveness make it an attractive choice for solving complex optimization problems. Through continuous research and development, PSO and its variants continue to evolve, offering new strategies for improving the performance and convergence speed of the algorithm. As computational challenges grow, the exploration and refinement of PSO and related swarm intelligence algorithms will undoubtedly play a crucial role in finding optimal solutions to complex problems.