In the previous article we introduced the framework of Mathematical Programming. Today we apply this framework to solve our very first problem. We also take this opportunity to learn new vocabulary that we'll use from now on.

Setting up the environment

There exist many Solvers. In this article we'll use SCIP, one of the most powerful non-commercial solvers. We'll also use Pyomo, one of the top Python libraries to interact with any solver.

The installation process of any Solver may be a bit tough, specially if it has to be compiled. Miniconda (or Conda if you prefer) provides the most straightforward installation as the solver is already compiled into a binary both for Linux and Windows systems.

Create a directory and copy the following conda environment into a conda-env.yaml file.

# conda-env.yaml
name: rook-problem  # Create a conda environment with this name.
channels:
    - conda-forge   # Download packages from this repository source.
dependencies:
    - python=3.12
    - scip=8.1.0    # The Solver. This downloads a compiled binary
                    # and adds makes it discoverable within the
                    # virtual environment.
    - pyomo=6.7.1   # The library to interact with any Solver.

Install and activate the environment. On Linux you can run the following command.

$ # This creates the virtual environment and installs libraries
$ conda env create -f conda-env.yaml
$ # This activates the virtual environment.
$ conda activate rook-problem

The framework with an example

Let's introduce the Rooks Problem. In chess, the Rook is a powerful piece that threatens all pieces in the same row and column.

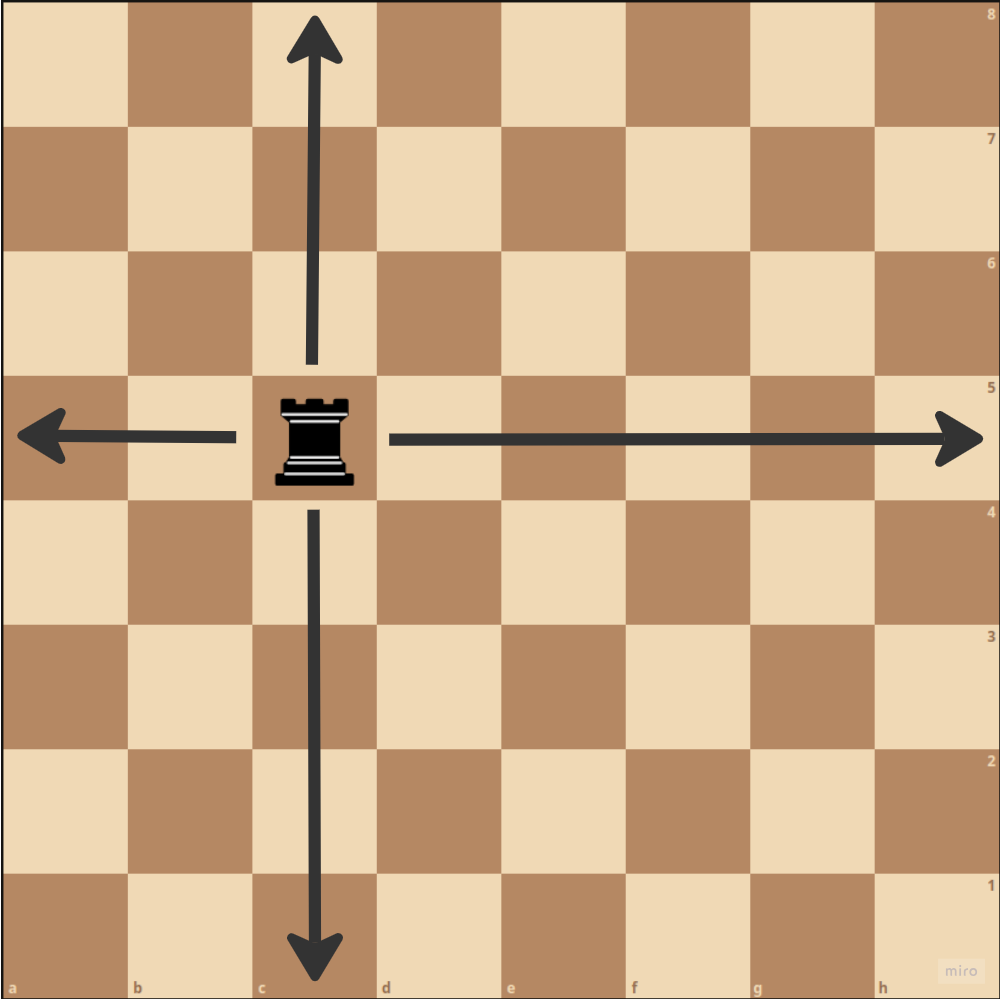
The problem is simple. What is the maximum number of nonattacking rooks that may be placed on a chessboard of 8 times 8 square?

Quick trial and error shows that the maximum number of rooks is eight. Here are four valid dispositions. Three of them, give an answer to our problem. The solution on the bottom right with just six rooks is valid in the sense that no rooks threaten each other, but it does not answer correctly our question.

Let's implement this problem in Mathematical Programming and let the computer answer this question for us.

Problem statement

As we did in the previous article, let's organize the problem into a document. In Mathematical Programming, this document is called a Problem. A Problem must answer:

• What is the goal? (we'll answer this question last)

• What data is at my disposal to reach this goal?

• What actions can I take to achieve this goal?

• Are there any requirements?

• Are there any forbidden actions?

Another synonym for Problem is Model. Let's initialize our first Model with Pyomo. Let's create a file rooks.py with the following lines.

from pyomo.environ import AbstractModel

model = AbstractModel(name='rooks_problem')

What does Abstract mean? Not rellevant now. Bear with it. We'll answer the question in subsequent articles.

What data do I have at my disposal to reach the goal?

The data of the problem are called sets and parameters. So, what are the sets and parameters? In this case, we have a set of columns and a set of rows. This models our is our chessboard.

from pyomo.environ import Set

model.columns = Set(
    name='rows',
    doc='Set of columns of a chess board',
    initialize=['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'],
)

model.rows = Set(
    name='rows',
    doc='Set of rows of a chess board',
    initialize=[1, 2, 3, 4, 5, 6, 7, 8],
)

# There are no parameters in this problem.

Argument doc is optional, but it is really helpful to communicate the meaning and usage to other teammates. It will prove very helpful later on for documentation later on. It is a good habit to fill it. Argument initialize provides the values of the set.

What actions can I take to achieve this goal?

Actions are called variables. Sets and Parameters are immutable and won't change in the future. On the other hand, the solver can (and does) choose the values of Variables to find the solution to our Problem.

So, what are the variables? For each square in the chessboard, we allow the solver to choose either if it places a rook or not. Thus, variables will be indexed by columns and rows. With the following syntax Pyomo creates one variable for each combination of elements of columns and rows. In total, there are 64 variables. The values of these variables are Binary as they only admit two options: 1 or 0.

from pyomo.environ import Binary, Var

model.place_rook = Var(  # Var stands for Variable
    # There is one variable for each combination of columns and rows.
    model.columns,
    model.rows,
    name='place_rook',
    doc=(
        'Binary value that equals 1 if a rook is placed in a square, and '
        'equals 0 otherwise.'
    ),
    domain=Binary,
)

As before, arguments name and doc are optional, but strongly recommended for documentation. It is a good habit to fill them. In doc we let the reader know our convention. The value of name doesn't need to match model.place_rook.

Are there any requirements? Are there any forbidden actions?

Requirements and forbidden actions are also called constraints. So what are the constraints?

1. At most there can be one rook per column. There are eight columns. Therefore, there are eight constraints.

from pyomo.environ import Constraint
from pyomo.core.expr.relational_expr import InequalityExpression

def constraint_at_most_one_rook_per_column(
    model: AbstractModel,
    column: str,
) -> InequalityExpression:
    """Limit the number of rooks per column to at most one."""
    number_of_rooks_in_column = (
        sum(model.place_rook[column, row] for row in model.rows)
    )
    return number_of_rooks_in_column <= 1

model.constraint_at_most_one_rook_per_column = Constraint(
    model.columns,
    name='at_most_one_rook_per_column',
    doc=constraint_at_most_one_rook_per_column.__doc__,
    rule=constraint_at_most_one_rook_per_column,
)

Constraints in Pyomo are initialized with the Constraint class. There is one constraint for each element in the set model.columns. Again, the name and doc are optional, but really helpful in future documentation. Finally, the rule that the constraint must follow is defined in function constraint_at_most_one_rook_per_column.

Don't be overwhelmed by type hints. They are there to let you understand what is going on.

First, as stated in the Constraint intialization, the function will be called for each value in the set model.columns. This value is in argument column.

The rule states that the number of rooks in the column must be less than or equal to one. The solver understands that not all choices of variables model.place_rook are valid. Only those that respect the rule.

Similarly, there are eight more constraints.

2. At most there can be one rook per row.

from pyomo.environ import Constraint
from pyomo.core.expr.relational_expr import InequalityExpression

def constraint_at_most_one_rook_per_row(
    model: AbstractModel,
    row: int,
) -> InequalityExpression:
    """Limit the number of rooks per row to at most one."""
    number_of_rooks_in_row = (
        sum(model.place_rook[column, row] for column in model.columns)
    )
    return number_of_rooks_in_row <= 1

model.constraint_at_most_one_rook_per_row = Constraint(
    model.rows,
    name='at_most_rook_per_row',
    doc=constraint_at_most_one_rook_per_row.__doc__,
    rule=constraint_at_most_one_rook_per_row,
)

What is the goal?

The goal is also called objective. What is the objective? Find the maximum number of rooks nonattacking that may be placed on our chessboard.

Next create an instance of Objective. The rule counts the number of rooks that are placed in the chessboard and we indicate the Solver to maximize this number.

from pyomo.core.expr.numeric_expr import LinearExpression

def number_of_rooks_in_the_board(model: AbstractModel) -> LinearExpression:
    """Count the number of rooks in the chessboard."""
    number_of_rooks_in_the_chessboard = sum(
        model.place_rook[column, row]
        for row in model.rows
        for column in model.columns
    )
    return number_of_rooks_in_the_chessboard

model.objective_function = Objective(
    rule=number_of_rooks_in_the_board,
    sense=maximize,
)

Hand the Problem to the solver

# Get an instance to solve
instance = model.create_instance()

# Use the SCIP solver
solver = SolverFactory('scip')

# Finally, solve the problem!
solution = solver.solve(instance, tee=True)

The argument tee is optional. If True, the solver brings us a nice log to double check our Problem and analyse the progress of the execution.

Report the best solution

After solving the problem, it's time to collect the fruits. First, we check if the solver found a solution, or had any error in the process. Second, we can access the actual values of varibles instance.place_rook with .value attribute.

# Did scip find a solution?
solution_found = (
    solution.solver.status == SolverStatus.ok
    or solution.solver.status == SolverStatus.warning
)
assert solution_found, 'The solver did not find any solution :('

rooks = [
    f'{column}{row}'
    for row, column in itertools.product(instance.rows, instance.columns)
    if instance.place_rook[column, row].value == 1
]

print(
    'Here is the best solution:\n'
    f'There are {len(rooks)} rooks in the chessboard.\n'
    f'Place rooks on positions {rooks}\n'
)

Run the script and evaluate the output

Run the script with python rooks.py . Here's the output.

$ python rook.py
SCIP version 8.1.0 [precision: 8 byte] [memory: block] [mode: optimized] [LP solver: Soplex 6.0.4] [GitHash: 6129793871]
Copyright (c) 2002-2023 Zuse Institute Berlin (ZIB)
...
original problem has 64 variables (64 bin, 0 int, 0 impl, 0 cont) and 16 constraints
...
SCIP Status        : problem is solved [optimal solution found]
Solving Time (sec) : 0.00
Solving Nodes      : 1
Primal Bound       : +8.00000000000000e+00 (2 solutions)
...
Here is the best solution:
There are 8 rooks in the chessboard.
Place rooks on positions ['a1', 'b2', 'c3', 'd4', 'e5', 'f6', 'g7', 'h8']

The output shows a lot of new information. No need to rush, we'll understand all of it in subsequent articles.

Let's just focus on three aspects. The problem has 64 variables (of course, our chessboard has 8 columns x 8 rows), all of them are binary (bin), and 16 constraints (just as we computed). The solver finds the optimal solution.

There are many valid solutions to this problem. Perhaps your execution finds another dispositon of the rooks. Don't worry, just double check that the answer makes sense.

Let's add more contraints!

We did it! I can read you mind, though... This solution is too obvious! No problem, let's add more constraints, just for fun!

from pyomo.core.expr.relational_expr import EqualityExpression

def constraint_no_rook_on_a1(model: AbstractModel) -> EqualityExpression:
    """No rock shall be placed on a1.

    Hope you give me a more interesting solution, Mr. Solver!
    """
    # Return type is now EqualityExpression
    return model.place_rook['a', 1] == 0

# Notice there's just one constraint, not indexed by any Set.
model.constraint_no_rook_on_a1 = Constraint(
    name='no_rook_on_a1',
    doc=constraint_no_rook_on_a1.__doc__,
    rule=constraint_no_rook_on_a1,
)

...
original problem has 64 variables (64 bin, 0 int, 0 impl, 0 cont) and 17 constraints
...
Primal Bound       : +8.00000000000000e+00 (2 solutions)
...
Here is the best solution:
There are 8 rooks in the chessboard.
Place rooks on positions ['h1', 'g2', 'c3', 'd4', 'e5', 'a6', 'b7', 'f8']

Now the log shows there are 17 constraints (previous 16 + 1 extra). We've got a different solution.

More challenges

Here are some challenges to make you think further }:)

• Add eight constraints so that it is forbidden to place rooks in the main diagonal (from top left to bottom right). Tip: Can you do it with just one Constraint instance?

• Add a constraint so that no more than 6 rooks can be placed in the chessboard.

• Try with a chessboard with other sizes. What about 10 rows and 20 columns?

• Let's make the problem so big that it takes a while to solve. Gradually scale the chessboard size with more rows and columns. See how it takes longer to solve the problem.

Feroucious learners out there: Can you solve the same problem with Queens instead of rooks? Good luck!

Share your experience in the comments below!

Attributions

• Chess-piece icons created by Freepik - Flaticon.

• Chess icons created by Freepik - Flaticon.

• Chess icons created by Eucalyp - Flaticon.

• Board games icons created by Freepik - Flaticon.

• Pawn icons created by Icon home - Flaticon.

• Rook icons created by Nsit - Flaticon.

• Strategy icons created by BZZRINCANTATION - Flaticon.

• Chess icons created by Freepik - Flaticon.

• Chess images generated with Lichess Editor.

• Approved icons created by juicy_fish - Flaticon.

• Close icons created by juicy_fish - Flaticon