Introduction to Graph Neural Networks

Have you ever stopped to think about how social media platforms like Facebook or Twitter recommend friends or posts to you? Or perhaps you’ve wondered how self-driving cars navigate through traffic? These are just a few examples of how GNNs are being used in our everyday lives.

What is a graph?

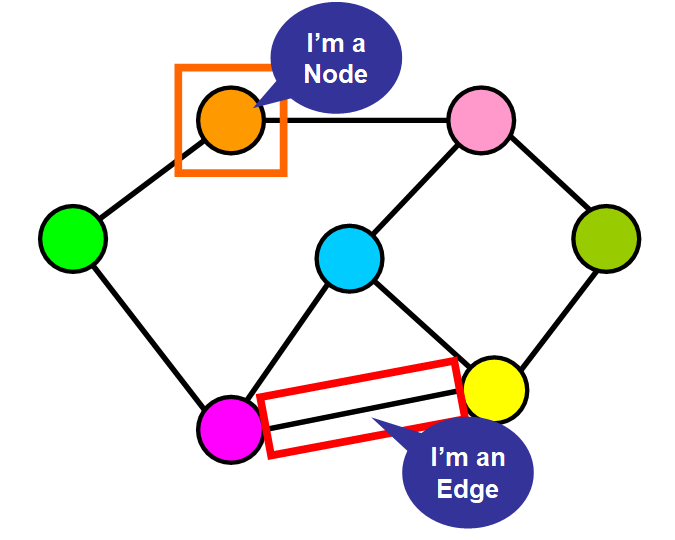
A graph is a collection of nodes (or vertices) that are connected by edges (or links). Nodes can represent anything, from people on a social network to atoms in a molecule. Edges represent the connections between these nodes. For instance, in a social network, an edge might connect two people who are friends.

How can graphs be used?

Graphs are a powerful tool for modeling relationships between things. They can be used to represent a wide variety of real-world data, including:

• Social networks (e.g., Facebook, Twitter)

• Citation networks (e.g., scientific papers)

• Recommendation systems (e.g., Amazon, Netflix)

• Traffic networks (e.g., Google Maps)

• Molecular structures (e.g., drug discovery)

What are graph neural networks (GNNs)?

GNNs are a type of neural network that can be used with graph data. They are a powerful tool for machine learning tasks that involve graphs, such as node classification, link prediction, and graph-level property prediction.

• Node classification: Node classification is the task of predicting a property of a node in a graph. For example, in a social network, we might want to predict whether a node is a user who is likely to churn (i.e., stop using the platform).

• Link prediction: Link prediction is the task of predicting whether two nodes in a graph will be connected by an edge. For example, in a social network, we might want to predict whether two users are likely to become friends.

• Graph-level property prediction: Graph-level property prediction is the task of predicting a property of the entire graph. For example, in a traffic network, we might want to predict the traffic congestion on a particular road.

Why are GNNs important?

GNNs are important because they can address the challenges of working with graph data. Unlike images, graphs can have variable sizes and shapes. GNNs can handle this by using a method that can handle arbitrary input shapes. Additionally, graphs are permutation invariant, meaning they can look different but have the same structure. GNNs are also permutation invariant. Finally, graphs are non-Euclidean, meaning there is no easy way to measure distance between nodes. GNNs do not rely on Euclidean distance.

Conclusion

GNNs are a powerful tool for machine learning tasks that involve graphs. They are being used in a wide variety of applications, from social media to self-driving cars. As GNN research continues to advance, we can expect to see even more innovative applications of this technology in the future.

I hope this blog post has given you a basic understanding of graph neural networks, we will discuss how GNNs work in more detail in part-2.

Important Links:

• https://blog.research.google/2024/02/graph-neural-networks-in-tensorflow.html

• https://www.geeksforgeeks.org/introduction-to-graphs-data-structure-and-algorithm-tutorials/