How Graph Neural Networks learn through message parsing
 Kanishk Munot
Kanishk Munot
In part one of our blog series, we explored the world of graphs and graph neural networks (GNNs). We learned that GNNs are a powerful tool for machine learning tasks involving graphs, like social networks and molecule structures. But how exactly do GNNs learn from these complex structures? This is where message passing comes in, and in this blog, we'll take a closer look at this critical concept.
Message Passing: Sharing Information in a Graph
Imagine a group project where students need to collaborate and share information. Message passing in GNNs works in a similar way. Each node in a graph acts like a student, and the edges represent communication channels. Nodes exchange information with their neighbors, learning from each other's data and updating their own understanding of the graph.
From Images to Graphs: Convolution Gets an Upgrade
We're familiar with convolutions in image processing, where learnable filters slide across an image to extract features. GNNs take this concept and adapt it to graphs. Instead of a grid-like structure, message passing focuses on the neighborhoods around each node. Nodes "talk" to their neighbors, gathering valuable information about the local structure of the graph.
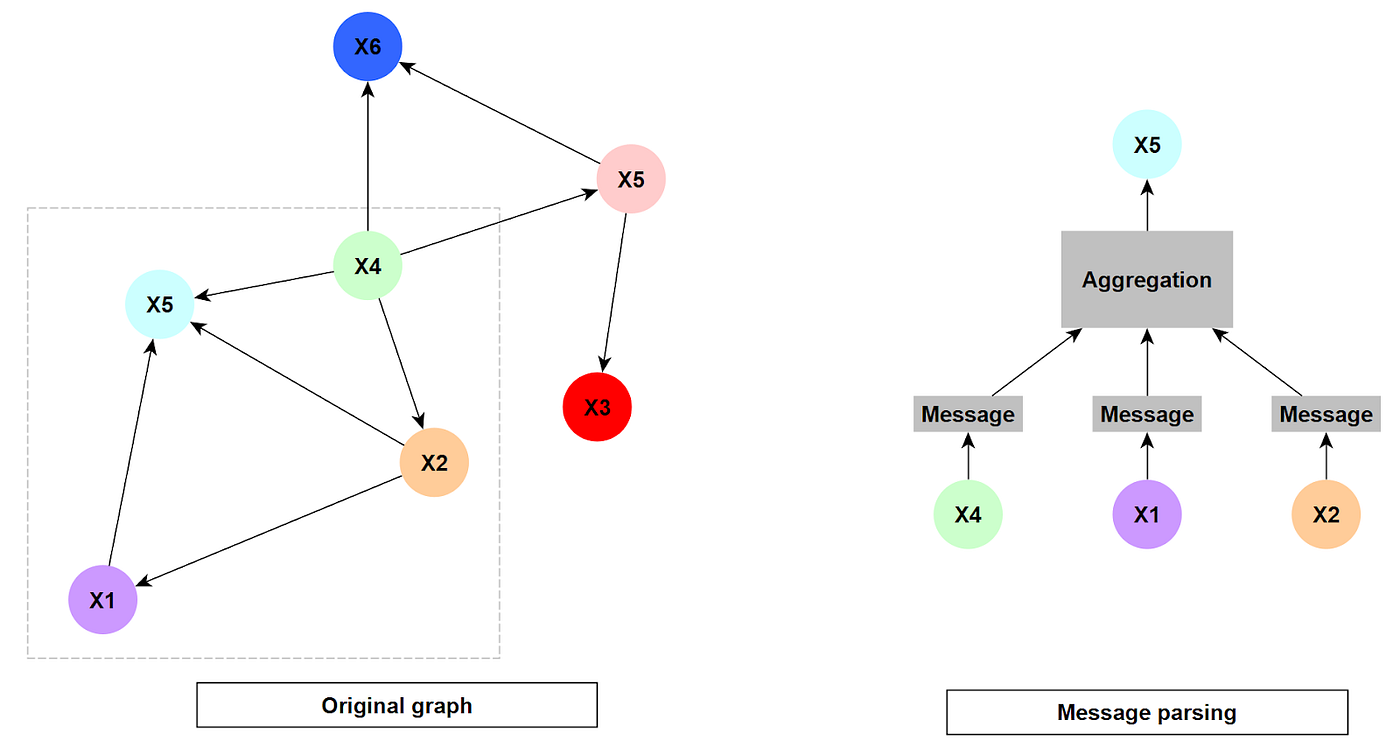
Message Passing Example
Think of a social network. A node might represent a user, and edges connect friends. During message passing, a user (node) receives information about their friends' interests, posts, and connections. This information is then used to update the user's own profile, potentially influencing their recommendations or content suggestions.
Message Passing in Action: Layers and Oversmoothing
GNNs often use multiple message passing layers. In each layer, nodes exchange information and update their states. This allows information to propagate through the graph, enabling nodes to learn not just from their immediate neighbors but also from more distant parts of the network. However, there's a catch: too many layers can lead to oversmoothing. Imagine a project where information gets passed around so much that everyone ends up with the same generic understanding. Similarly, with too many message passing layers, node embeddings (compressed representations of a node's information) can become indistinguishable.
The Math Behind the Magic: Aggregation and Update
To understand message passing mathematically, we need to consider two key operations: aggregation and update. Aggregation combines the information received from neighboring nodes. Think of it as summarizing the key points from your project group discussions. The update operation then merges this aggregated information with the node's current state. This combined knowledge becomes the node's updated understanding of the graph.
Generalizing the convolution operator to irregular domains is typically expressed as a neighborhood aggregation or message passing scheme. With \(\mathbf{x}^{(k-1)}_i \in \mathbb{R}^F\) denoting node features of node \(i\) in layer \((k-1)\) and \(\mathbf{e}_{j,i} \in \mathbb{R}^D\) denoting (optional) edge features from node \(j\) to node \(i\), message passing graph neural networks can be described as :
\( \mathbf{x}_i^{(k)} = \gamma^{(k)} \left( \mathbf{x}_i^{(k-1)}, \bigoplus_{j \in \mathcal{N}(i)} \, \phi^{(k)}\left(\mathbf{x}_i^{(k-1)}, \mathbf{x}_j^{(k-1)},\mathbf{e}_{j,i}\right) \right),\)
where \(\bigoplus\) denotes a differentiable, permutation invariant function, e.g., sum, mean or max, and \(\gamma\) and \(\phi\) denote differentiable functions such as MLPs (Multi Layer Perceptrons).
Note: The equation has been directly taken from this post
Conclusion: Message Passing - The Engine of GNNs
By understanding message passing, we gain a deeper appreciation for how GNNs function. This core concept allows nodes to learn from each other and build a comprehensive understanding of the graph structure. As we explore different message passing variants in future posts, we'll see how GNNs can be tailored to tackle a wide range of machine learning tasks that involve complex, interconnected data.
Important links:
• https://towardsdatascience.com/introduction-to-message-passing-neural-networks-e670dc103a87
• https://www.sciencedirect.com/science/article/pii/S2666651021000012
Subscribe to my newsletter
Read articles from Kanishk Munot directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by