Introduction

When I scrolled through my Instagram feed, I saw several videos of a Flipper Zero cracking PIN locks with the brute-force method. Others were showing some shell-ish code on a smartphone. One of those videos presented two old iPhones connected with a cable to each other. Then one of the devices executed a script which cracked the five digit pin after a few seconds. What really caught my attention was not the fast execution time of a few seconds, no, it rather was the fact that the devices were connected with different coloured cables (one was black, the other was white). Unfortunately, the creator did not care about this "small" mistake.

What is brute-force?

Brute-force refers to a problem-solving paradigm which systematically checks each candidate if it meets a certain criteria. It is the most general and inefficient searching methods to use, as the time complexity is proportional to the amount of candidates.

Example 1

Let us assume userdata to be a list of 10.000.000 user accounts with each having personal information, such as email and user-id. For this example we assume additionally following things:

1. userdata is chaotic

2. Each entry in userdata has a position and user-id. The position is the place where one entry is stored and the user-id is a unique integer generated at the user creation

We want to find the email of Joe with the user id 42. If the set was ordered we could just go at place 42, as Joe is at the place 42 and get his email. The brute-force algorithm is fairly simple, as we start at the beginning and iterate through the data until we find a match.

As we cannot tell where our user with the number 42 is located, we can either be lucky and hope that by accident Joe is right at the beginning or we have a bad day and joe is the last element of our long list.

Brute-force is simply speaking an algorithm which systematically iterates through data to find a certain element

Why is brute-force bad?

Our model list userdata has 10.000.000 entries. If Joe was element 999.999, we would need to go through 999.999 elements to find him. Hence, the amount of elements is proportional to the time.

The time complexity will be thus:

Where n is the number of elements

What has this to do with PINs?

The FlipperZero Videos utilised the same approach of cracking a pin. They all tried 5-10 combinations and "successfully" found the right combination.

Let us go a bit deeper and prove why brute-force is a bad choice.

Pin Generation

Before applying brute-force algorithms, we need to generate random PINs. Those PINs will be used as an automatic input for the brute-force function which will be discussed later.

Requirements:

• Variable PIN length

• PIN is a python tuple, because integer variables cannot start with one or more leading zero. A PIN like 0423 would be transformed to 423. Thus, we will use for each PIN a tuple where each element is a digit.

First, we will need to do some importing and installing in our venv with python -m pip install <name>.

# Import statements for later :) 
import time 
import tqdm 
import matplotlib.pyplot as plt 
import pandas as pd 
import numpy as np 
import random
from pprint import pprint as pp # We will use prettyprint to have cleaner print statements

Next we will code our PIN generator function:

def generate_random_pin(length):    
    """Generates a random pin as a tuple with a certain length"""        
    pin = []    
    for _ in range(length):        
        pin.append(random.randrange(0,9))    
    return tuple(pin)

One of the main functionalities of my code is that you can experiment with different pin lengths. This will be useful later if we improve brute-force and do some testing. I prefer tuples, since tuples cannot be modified once created, as we will never modify the PIN. It also gives us the security that the integrity of the PIN is guaranteed.

pin = generate_random_pin(4)
pp(pin)

When executing, the four digit pin will be randomly generated. From now on, we will assume that pin is the pin of our target device

Following code will check if our pin is a tuple and if the pin has only numbers between 0 and 9 of the type int. Since it is best-practice to introduce methods once a code needs to be executed at least twice, I designed this routine for later use.

def pin_checker(pin:tuple):    
    """Checks the validity of a pin and returns the pin if the pin is valid"""    
    if len(pin) == 0: # Empty pins should not exist        
        raise ValueError("Pin cannot be empty!")    
    for j in pin:        
        if type(j) != int: # If the pin is not an interger, throw error            
            raise TypeError("Please only provide Integers. \n\n Wrong character: "  + '"' +str(j) +'"' + " \n\nData type: " + str(type(j)))        
        if j < 0 or j >= 10: # if the number is not decimal, throw an error            
            raise ValueError("PIN Numbers can only be between 0 and 10 of the type Integer!")        
        return pin

Statistics on brute-force

Many people on Social Media may agree that cracking a 4 digit PIN is no rocket science, since it is only 4 digits long.

Indeed, we will need no rocket science to proof that a 4 digit pin is pretty secure in real life under certain circumstances. Before calculating the combinations and the probability of cracking a four digit personal identification number, we assume following things to be true:

1. The time-complexity of brute-force is O(n).

2. The Personal Identification Number is within the decimal system

3. Our target PIN utilises any decimal number

4. There are no restrictions on consecutive patterns like 9999 , 4242, 1234 etc.

5. Our device locks after 5 wrong attempts

6. An attempt is the act of entering the pin in the system.

Combinations of a PIN

Knowing the combinations of a PIN or password are incredibly important to know, since one wants to calculate the possibility of a cracked password, as well as the time complexity behind that.

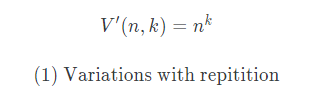
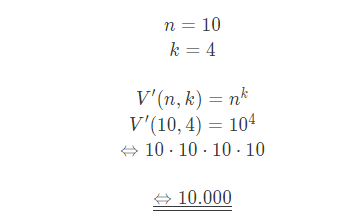
Resulting in 10.000 possible ways to arrange the numbers 0-9, we can clearly see that it is already very unlikely that one can unlock the phone in the first 5 attempts. If you have 5 digits, our variations will increase by the factor 10 (!)

Conclusion 1: It looks kind of bad for us...

In the worst case, we need 10.000 attempts to crack a PIN. This is much.

Possibility of cracking the pin within 5 times:

Imagine, we start with 10.000 variations. Our code begins at 0000 and goes all the way up to 10.000.

Once the first pin is entered, the amount of variations decreases by one. Meaning we have to deal only with 9999 variations

To calculate the possibility for 5 attempts and 10.000 variations, we need to create our own equation.

One in every 2000 devices can be cracked within 5 attempts. This is incredibly low and shows that it is rather unusual to crack a phone within 5 attempts. After the 5th attempt your device is most likely locked (like in apple or Samsung afaik).

System information

Every code that I provide was properly tested and executed on my home lab. Since brute-force needs high computational power, I decided to run this code in a bare metal environment where not many other processes can interfere with my code. Any duration given in this report refers to my home lab environment.

My home lab hardware*:

• MSI cubi5 Barebone PC

• Intel Core i7 12th Gen., 10c/12t

• 32 GiB DDR4 SODIMM RAM

• 1 TiB NVMe Storage, WD_BLACK SN850X

My software:

• Proxmox PVE for virtualisation

• LXC Container with JupyterHub (12GiB RAM, 8 Cores, 128 GiB SSD)

In order to avoid any performance issues, I stopped all LXC containers except of the Jupyter Server. This setup could handle 10 digits within a reasonably acceptable time.

If you have enough time and a similar setup, 10 digits can be handled well.

Remember: This runs inside a LXC container and NOT on Windows.

I haven't tested any of this on Windows or Mac setups but there should be no issues when using "normal" pin sizes. Usually a four digit pin should be handled well enough on most of the machines.

My advice:

• Stick to reasonable PIN sizes (4 is what is used most of the times)

• Only experiment with different sizes if you are sure your machine is powerful enough

• Try Google Colab or similar for testing purposes

• If your PC cannot handle 4 digit PINs, just read along :)

Everything I do is well-documented so that there is no need to run the script.

Brute-Forcing

Our crack_pin function is responsible for the cracking of PINs. Essentially, this script takes a pin of any length as input, converts it to a string for easier comparison and length check and finally returns a dictionary with the statistics around the brute-forcing. Needless to say it is recommended to provide PINs with low pin sizes. I tried 10 and it took some time to run on my setup.

def crack_pin(target_pin:tuple):    
    # Starts timer to measure the duration    
    time_started = time.time()    

    for j in target_pin:        
        if j < 0 or j >= 10 or type(j) != int:            
            raise ValueError("PIN Numbers can only be between 0 and 10 and of the type Integer!")

    target_pin_str = ''.join(map(str, target_pin)) #Convert tuple to string for easier comparison    
    pin_length = len(target_pin_str) 
    guess = 0 
    result = []

    for _ in range(10**len(target_pin)):                
        # Generate the current guess as a string, padded with zeros if necessary        
        guess_str = str(guess).zfill(pin_length)                
        if guess_str == target_pin_str:
            for i in guess_str:                
                result.append(int(i))
        guess+=1
    return {"attempts":guess, "pin": tuple(result), "max_iterations": 10**len(target_pin), "execution_time_in_s": time.time() - time_started}

Combining our crack_pin function with our generate_random_pin function from earlier, we can both generate and crack our generated pin.

pin = generate_random_pin(4)
pp(pin) # prettyprint is way better to use. It just formats the outputs nicer. Alternatively, use the print() command
bf_results = crack_pin(pin)
pp(bf_results)

Wrapping up

In part one we have successfully covered the basics of the science behind brute-force and have written a fundamental program which allows us to brute-force pins.

In part two we will optimise our brute-force code and make it more realistic.

Can we even improve our probabilities?
What about time complexity?

Stick around for part two

* This is my personal home setup. I mentioned this for transparency and for reference, as the hardware and software is integral to what the outcome is. I am not affiliated with any brand nor I receive any payment in any form.