Unraveling the Fibonacci Mystery

In this blog lets try and understand how we can solve the 509. Fibonacci Number using recursion with code in python and golang.

Problem statement

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

$$F(0) = 0, F(1) = 1$$

This in general translates to:

F(n)=F(n−1)+F(n−2)for n > 1.

Given n, calculate F(n).

Examples

Example 1:

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Example 2:

Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Example 3:

Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

Constraints

0 <= n <= 30

Intuition

The fibonacci is a classic problem that can be solved using recursion. In the recursion blog we understood how to use recursion. Lets understand how we can solve this problem using the following steps:

• Identify actual problem: find fibonacci(n)

• Identify sub-problem: in order to find fibonacci(n) we will have to find fibonacci(n-1),fibonacci(n-2).....fibonacci(1) . So, fibonacci(n-1),fibonacci(n-2) ,etc will be the sub-problems.

• Trust that the base function works: we trust that the function fibonacci works for all sub-problems and will give correct answer.

Link actual and sub-problem: as it is already specified in the problem statement, actual and sub-problems are linked like this:

$$fib(n)=fib(n-1)+fib(n-2)$$

• Identify base condition: Since we can't find fibonacci of -1 as per constraints, we can say that:

    if n<=1:
        return n
  

  This will make sure our recursion does not go beyond fibonacci(0).

Solution

Code in python

class Solution:
    def fib(self, n: int) -> int:
        # base case
        if n<=1:
            return n
        # recursive case
        return self.fib(n-1)+self.fib(n-2)

Code in Go

func fib(n int) int {
    // base case
    if n<=1{
        return n
    }
    // recursive case
    return fib(n-1)+fib(n-2)
}

Time and space complexity

Time Complexity:

$$O(2^n)$$

this is because for each recursive function call we make two other recursive calls.

Space complexity:

If you observe closely, although we are not employing any data structure, due to recursion, the compiler allocates space on the heap for each recursive call. Consequently, the space complexity is determined by:

$$O(n)$$

Recursive call stack

Here's the recursive call stack for fibonacci(5)

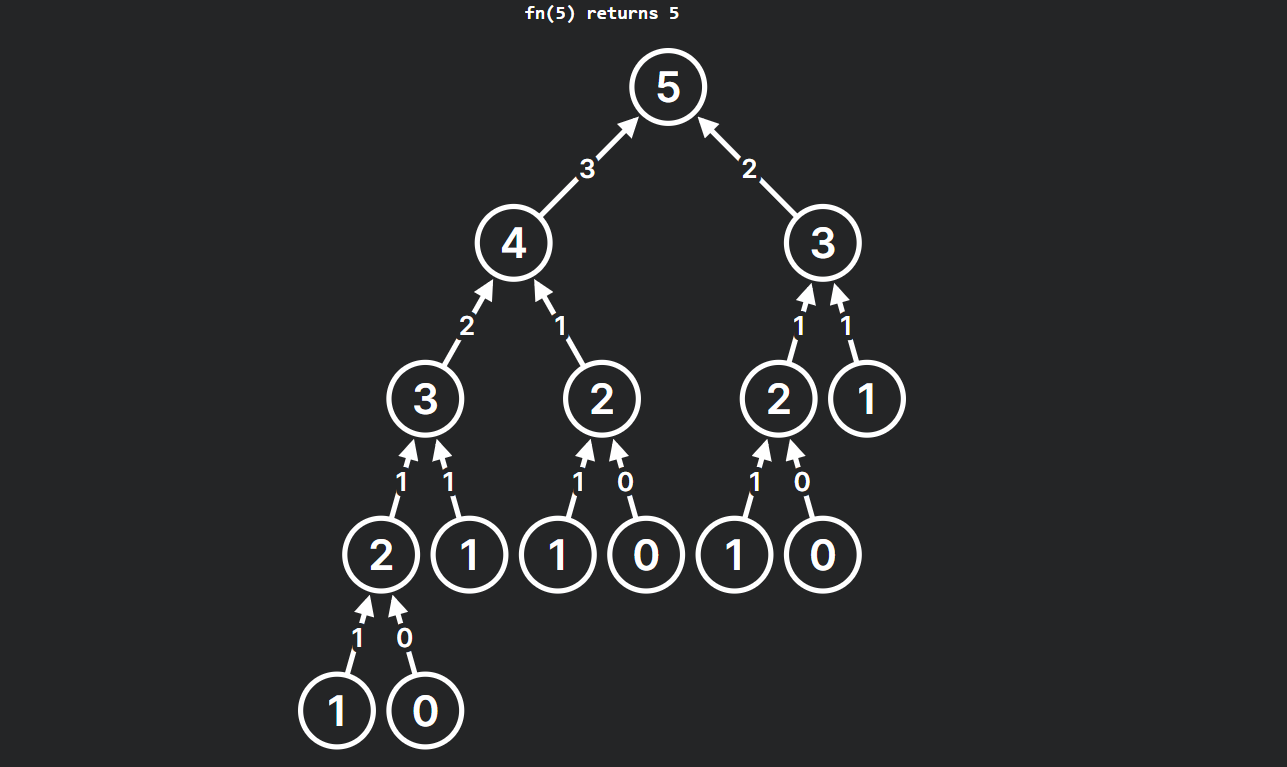
Conclusion

Now that you've explored both Python and Golang solutions for finding the Fibonacci sequence, you have a powerful toolkit at your disposal! Remember, recursion can be a great approach for many problems, but consider iterative solutions for larger values of n due to potential stack overflow issues with recursion.

The Fibonacci sequence is just a stepping stone. The concepts of recursion and iterative solutions are applicable to various problems in computer science. So, keep practicing, explore different problems, and unleash the power of recursion (or iteration) in your programming endeavors!