Example of Ad Hoc problem in DSA questions : Many approaches, some better than others ;

The Prologue

I was trying to get back into learning more about Data Structures and Algorithms, a topic that I thoroughly enjoyed in the past - both the ups and the downs. So I started working on a question that I left at almost completed status 2 months ago. The code that I wrote then was ugly and somewhat lengthy ( unnecessarily ), so I started having a dig at it again with a fresher mind. So I started reading the question and doing it all over from scratch again.

Objective of this blog post:-

• Understanding a class of problems called Ad Hoc problems

• Through the example of a suitable question

• Intuition behind the solution

• 2 approaches to the same problem,one better than the other

Ad Hoc problems

Ad hoc problems in Algorithms refer to those problems that lack a standardized or well-defined solution methodology. These problems often require creative and improvised approaches, leveraging many algorithmic techniques and heuristics tailored to that specific problem instance rather than relying on established algorithms or theories.

The Question

Codeforces has a lot of these ad hoc problem for beginners rated around 800 - 1100. We'll be looking at this particular one :-

Codeforces problem 1890A Doremy's Paint Part - 3

Constrains

Expected Output

Sample Test cases and Output

( You can copy paste the values and check if you're getting the correct answers )

5
2
8 9
3
1 1 2
4
1 1 4 5
5
2 3 3 3 3
4
100000 100000 100000 100000

Yes
Yes
No
No
Yes

Understanding the Question

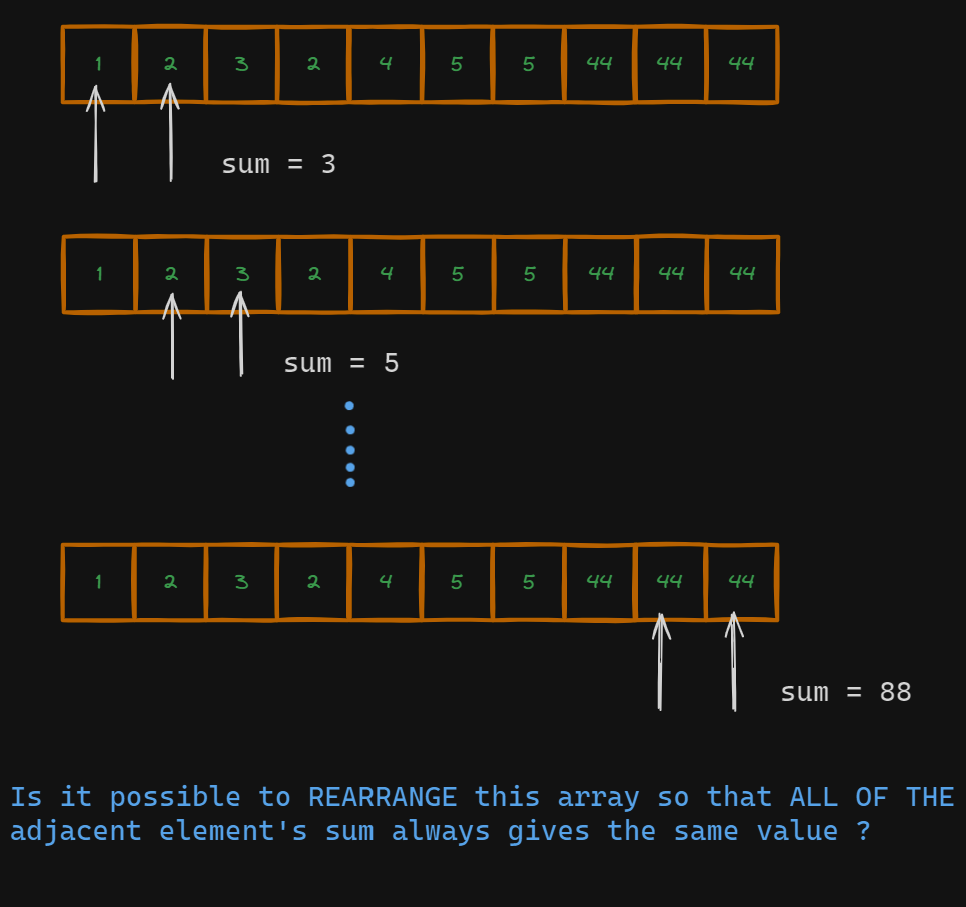
As straightforward as that.

Naive Idea :- Brute Force

Algorithm :-

1. Construct all possible arrangements of array

2. See if the adjacent elements sums to the same value

Theoretically to construct all possible arrangements, it'll be O( n! ) !!!!;

But you could argue that we'd be able to detect if there is a sum mismatch within few iterations and the ammortised cost might degenerate to some reasonable polynomial time, and I'd say " It's still really bad, i think." or "Can you prove it ?"

Logic - I

( I came up with it when I was burnt out ; So the logic isn't the best is pretty bad, but we'll make it better; TRUST ME ON THAT or abandon ship and come up with new approach later )

I'll explain why this always works and the key intuition for arriving at it, in the next section. The purpose of the below algorithm is only to show that many working and valid solution to ad hoc problems are sub optimal, and how we can come up with something better.

Algorithm :-

1. Check if n = length( array_given) is even or odd

2. If n is even

   1. count the number of times you see first element

   2. count the number of times you see another distinct element

   3. if at all you see an element different from the previously seen distinct elements, then the array is not good

   4. if counters follows the following pattern it is good

      1. either of the counts == n ( all n elements are same ) => Array can be permuted to be good

      2. Both of the counts are equally n/2 => array can be permuted to be good

   5. If the counters does not follow them, then they can't be made good.

3. if n is odd

   1. count the number of times you see first element

   2. count the number of times you see another distinct element

   3. if at all you see an element different from the previously seen distinct elements, then the array is not good

   4. if counters follows the following pattern it is good

      1. either of the counts == n ( all n elements are same ) => Array can be permuted to be good

      2. One count is (n+1)/2 - 1 and other count is (n+1)/2 => array can be permuted to be good

   5. If the counters does not follow them, then they can't be made good.

Now that I gave a cringe attack to all reading, allow me to go even further and show the ugly code I worked on for a good one hour. I'll explain later why this code is so bad.

Example Implementation for Logic - I

int a[100];
void old_solution(){
    int t,n,x,y; cin >> t;
    // x is the first element
    // y is the first element that is different from x

    while(t--){
        cin >> n; 
        int cnt1 = 0, cnt2 = 0;
        // if n == even
        if(n%2==0){
            for(int i=0;i<n;i++) cin >> a[i] ;

            int flag = 0, fn = 0;
            // cnt1 count of first elem
            x=a[0]; cnt1++; 
            for( int i=1; i<n; i++){
                if(a[i]==x)cnt1++;
                else{
                    if(!flag){ y=a[i];cnt2++;flag=1;} // first time seeing this 
                    else{
                        if(a[i] == y)cnt2++;
                        // see an element different from x and y
                        else { fn = 1;break; }
                }}
            }
            cout << cnt1 << cnt2 << "\n" ;
            if(fn){cout << "NO\n" ;}
            else{
                if(cnt1 == n || (cnt1 == n/2 && cnt2 == n/2) )cout << "YES\n" ;
                else cout << "NO\n";
            }
        }else{
            for(int i=0;i<n;i++) cin >> a[i] ;
             int flag = 0, fn = 0;

            // cnt1 count of first elem
            x = a[0]; cnt1++; 
            for( int i=1; i<n; i++){
                if(a[i]==x)cnt1++;
                else{
                    if(!flag){y=a[i];cnt2++;flag=1;} // first time seeing this 
                    else{
                        if(a[i] == y)cnt2++;
                        // see an element different from x and y
                        else { fn = 1;break; }
                }}
            }
            if(fn)cout << "NO\n" ;
            else{
                if(cnt1 == n || (cnt1 == (n+1)/2 && cnt2 == (n+1)/2 + 1) || (cnt1 == (n+1)/2 + 1 && cnt2 == (n+1)/2) )cout << "YES\n" ;
                else cout << "NO\n";
                }
        }
    }
}

Logic - II

Now that I was out of DSA for a month and started approaching this with a fresh mind, I hopefully did better. It took 30 minutes to implement, with the annoying errors and edge cases that I forgot to take care about.

Key Intuition

If we look at any good array :-

$$b_0+b_1=b_1+b_2\Rightarrow b_0=b_2$$

$$\\b_1+b_2=b_2+b_3\Rightarrow b_1=b_3$$

But we also know,

$$\\b_2+b_3=b_3+b_4\Rightarrow b_2=b_4$$

$$\\b_3+b_4=b_4+b_5\Rightarrow b_3=b_5$$

So combining the 2, we get :-

$$b_0 = b_2 = b_4 \cdot\cdot\cdot = b_{2k}$$

$$b_1 = b_3 = b_5 = \cdot\cdot\cdot = b_{2k + 1}$$

By Principle of Induction it can be induced from the first system it's self that there can only be at most 2 distinct elements in the array. The mathematical proof isn't much but I leave that to the CS grads 🙂;

So to visualize :-

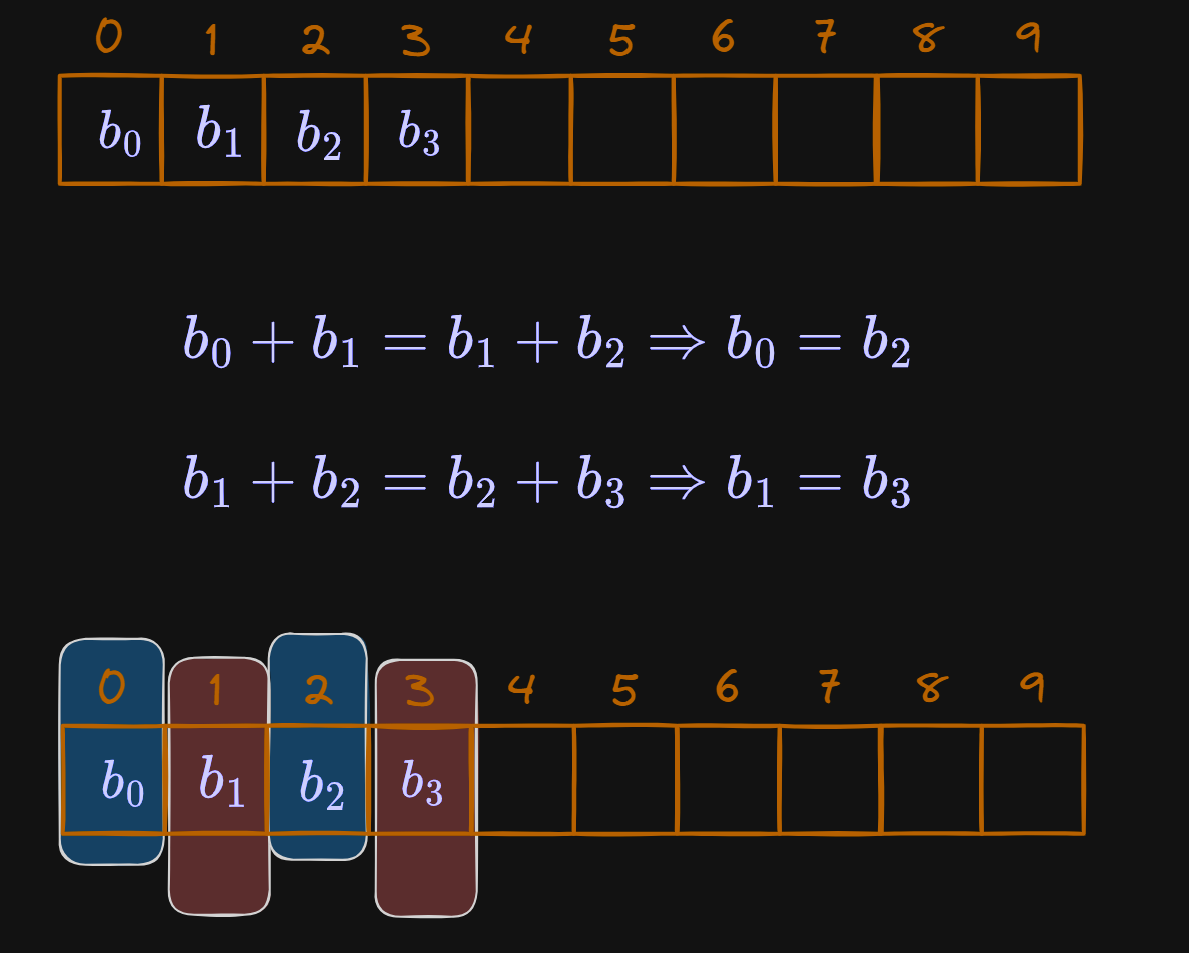
So the Principle of Induction visualized would something like :-

same elements are in same colour.

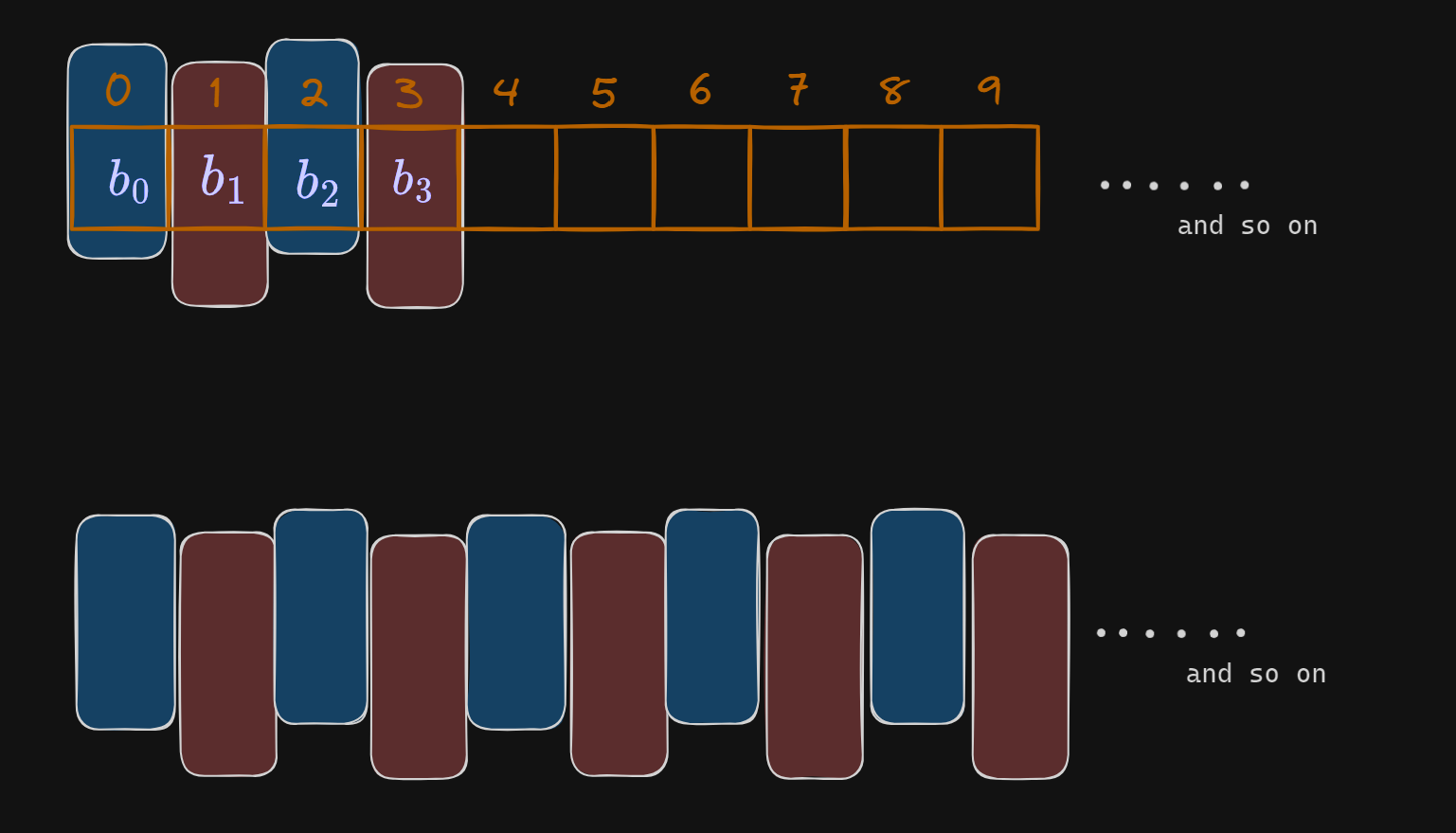
So this gives us the most important intuition for this question :-

There can only be 2 DISTINCT elements AT MOST in the array. Only then can we make an arrangement where all the adjacent elements sums to the same value.

Algorithm

1. Check if the number of distinct characters are less than or equal to 2.

   ( If the number of distinct characters are greater than 2 => NOT POSSIBLE ; )

   ( If the entire array was of same elements => IT'S POSSIBLE ; )

2. Check if the difference between count[ 1st element ] - count[ different element ] is at most 1. ( if it is => POSSIBLE ; If it's not => NOT POSSIBLE ; )

   THAT'S IT !!

Example Implementation for Logic - II

int arr[100];
void simple_solution(){

    // 1. check if distinct elements are 1 or 2
    // 2. check if c1-c2 is 0 or 1
    //  ONLY THEN  can the array be made good

    int t,n;
    cin >> t;
    while(t--){

        int seen1,seen2,started=0; int c1=0,c2=0; int no_flag=0;

        cin >> n;
        for(int i=0;i<n;i++){
            cin >> arr[i]; 
            if( started ){ 
                if( started==1 && arr[i] != seen1 ) { seen2=arr[i]; started++; }
                else{
                    // no flag triggered only when we see an element 
                    // different from seen1 and seen2
                    if( arr[i] != seen1 && arr[i] != seen2 ) { no_flag = 1; /* break; */ } 
                    if(arr[i]==seen1)c1++; else c2++ ; 
                } 
            } 
            else{ seen1 = arr[i] ;started++ ; }  
        }

        if( no_flag ){ cout << "NO\n"; continue; }
        if( started == 1 ){ cout<<"YES\n"; continue; }

        if(abs(c1-c2)<=1){ cout<<"YES\n"; }
        else { cout << "NO\n";}
    }
}

Why was Logic - I worse ?

Biggest reason

There was no need to have 2 different cases, since the central idea anyway independent of weather the size of array is even or odd .

I got the key intuitions of at most only 2 distinct elements for logic - I, but the framing the logic was unnecessarily tedious.

Code was still needlessly long

ODD CASE

• If counters follows the following pattern, it is good

  1. case where all elements are same

  2. One count is (n+1)/2 - 1 and other count is (n+1)/2 => array can be permuted to be good

     => difference in counts = 1

EVEN CASE

• if counters follows the following pattern, it is good

  1. case where all elements are same

  2. Both of the counts are equally n/2 => array can be permuted to be good

     => difference in counts = 0

These two rules could have been tested for their DIFFERENCES which would avoid lines like :-

if(cnt1 == n || (cnt1 == (n+1)/2 && cnt2 == (n+1)/2 + 1) || (cnt1 == (n+1)/2 + 1 && cnt2 == (n+1)/2) )cout << "YES\n" ;

Better code :-

if(cnt1 == n || abs(cnt1-cnt2) <= 1 ) cout << "YES\n" ;

In my defence though, normally I don't make THIS dumb mistakes, I make DUMBER , but during that time I was trying to develop the skill of splitting a problem into smaller sub problems and then learning to use dynamic programming to recursively tackle all the sub problems. And I didn't really think enough to see a better way. Once I got the intuition of there being only at most 2 elements in the array, I was in auto pilot mode, which explains those absurdly long lines.

Important Learnings from both Mistakes and Successes

1. We didn't have to ARRANGE the array to know IF it was possible.

2. Don't forget to reset the value of counters and flags for each test case.

3. Even if you know the answer before codeforces finished giving you the inputs, IT WILL STILL SHOVE IT DOWN YOUR THROAT.

   • If you look carefully :-

   •            else{
                   // no flag triggered only when we see an element 
                   // different from seen1 and seen2
                    if( arr[i] != seen1 && arr[i] != seen2 ) { no_flag = 1; /* break; */ } 
                    if(arr[i]==seen1)c1++; else c2++ ; 
               }
     

   • The break is commented out. We know as soon as we see a third distinct element in the array we can say the answer is NO. But at least in codeforces, it will still feed you inputs and therefore you need to take those inputs anyway. That is why I am using flag variable to detect if ever a third distinct element was seen => no_flag and still accepting the elements after I toggle the no_flag

4. Don't be shy to use vectors for counting 2 elements. The code gets simpler.

5. If you're burnt out, touch grass for a while. BREATHE. Live. Otherwise you'll solve problems but you won't get better.

6. Even if you get the LOGIC quickly after reading the question, don't get in your head, you can still RUIN the implementation.

Closing statements

• Many of the lower rated problems in Codeforces often are ad hoc problems. Many of them are exercises for developing an ability to develop LOGIC into IMPLEMENTATION in CODE .

  • https://www.tle-eliminators.com/cp-sheet <--- Very good list of codeforces problems to start out in developing coding skills to implement LOGIC

• Finally :-

Inspirations from a Japanese coder I admire - Kotatsugame ; He is really good with these " converting logic into BETTER code " apart from being a god tier coder with humble beginnings; On inspecting his way of writing code carefully, I get a a lot of inspirations and ideas.

( I heard subscribing to his channel and watching him code helps you to clear the DSA round in placements. )

Thank you for reading,

CPPTry_Hard__ ;