Distribution of data in NoSQL Databases - Part 1

Introduction

Amazon Dynamo and Cassandra whitepapers are the blueprint for NoSQL wide column databases.

These databases solve many problems which aren't intended to be solved in relational databases. One of the predominant feature is Horizontal Scalability. It is achieved via the efficient Distribution of data.

If you know consistent hashing already, feel free to close this article.

Predominant solution for this problem in relational world is sharding of data where the client application manages the data across respective shards. As the number of shard grows, maintenance complexity will grow in any systems.

Let's see how the Distribution of data happens in detail like how to solve the feature request from scratch.

---

Distribution of data

The ability to handle the increase in volume of data is the basic criteria for the database to be scalable.

Hence, the architecture of these database are distributed.

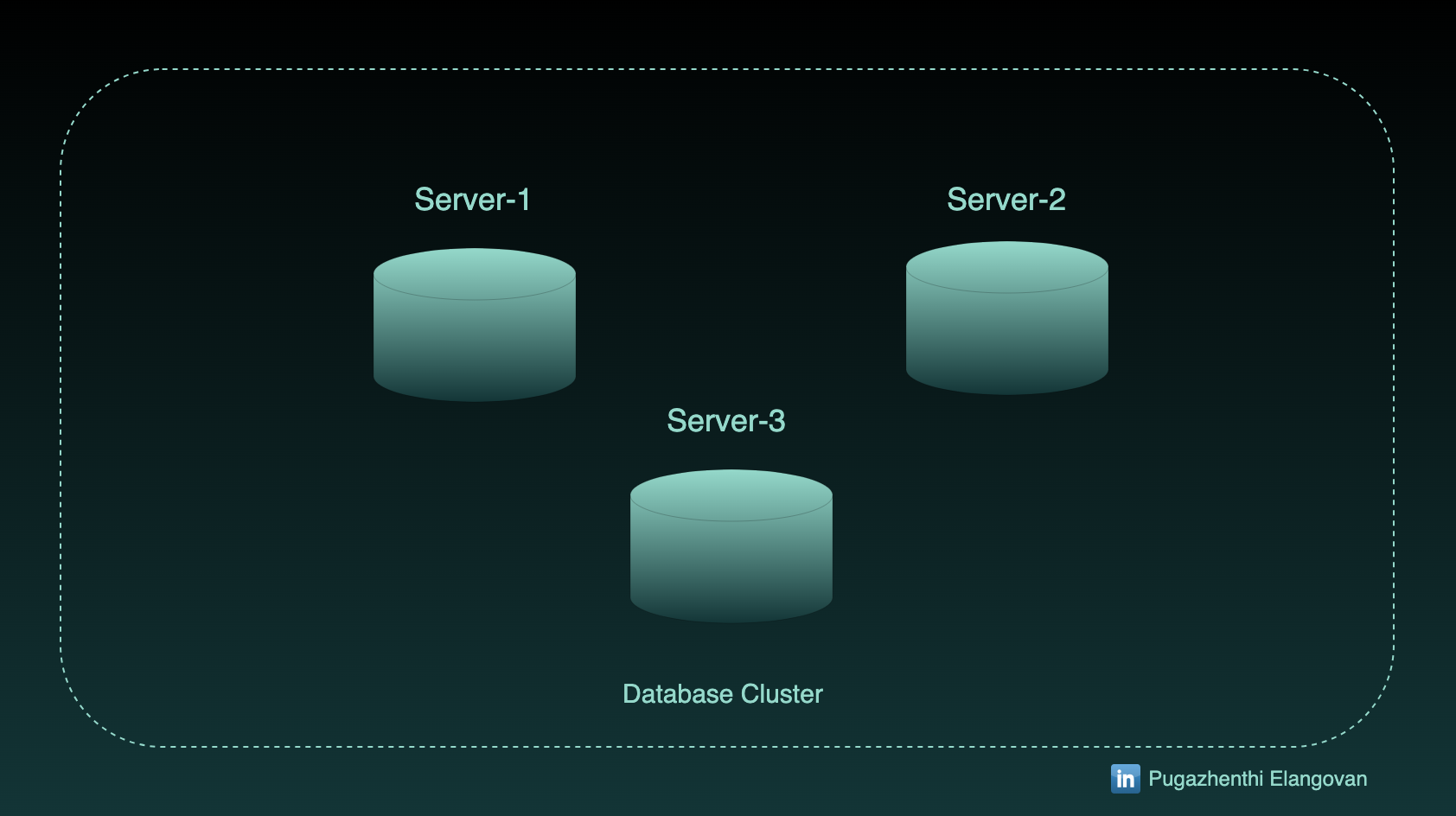
How do they identify the node of the particular smallest unit of data, row (column family / record)?

-> When you insert/query the record, the database should figure out the node in which the data must reside.

Hashing using server count

Let's start. How we solve it using simple solutions.?

Hashing is the technique been used to solve this problem in memory data structures.

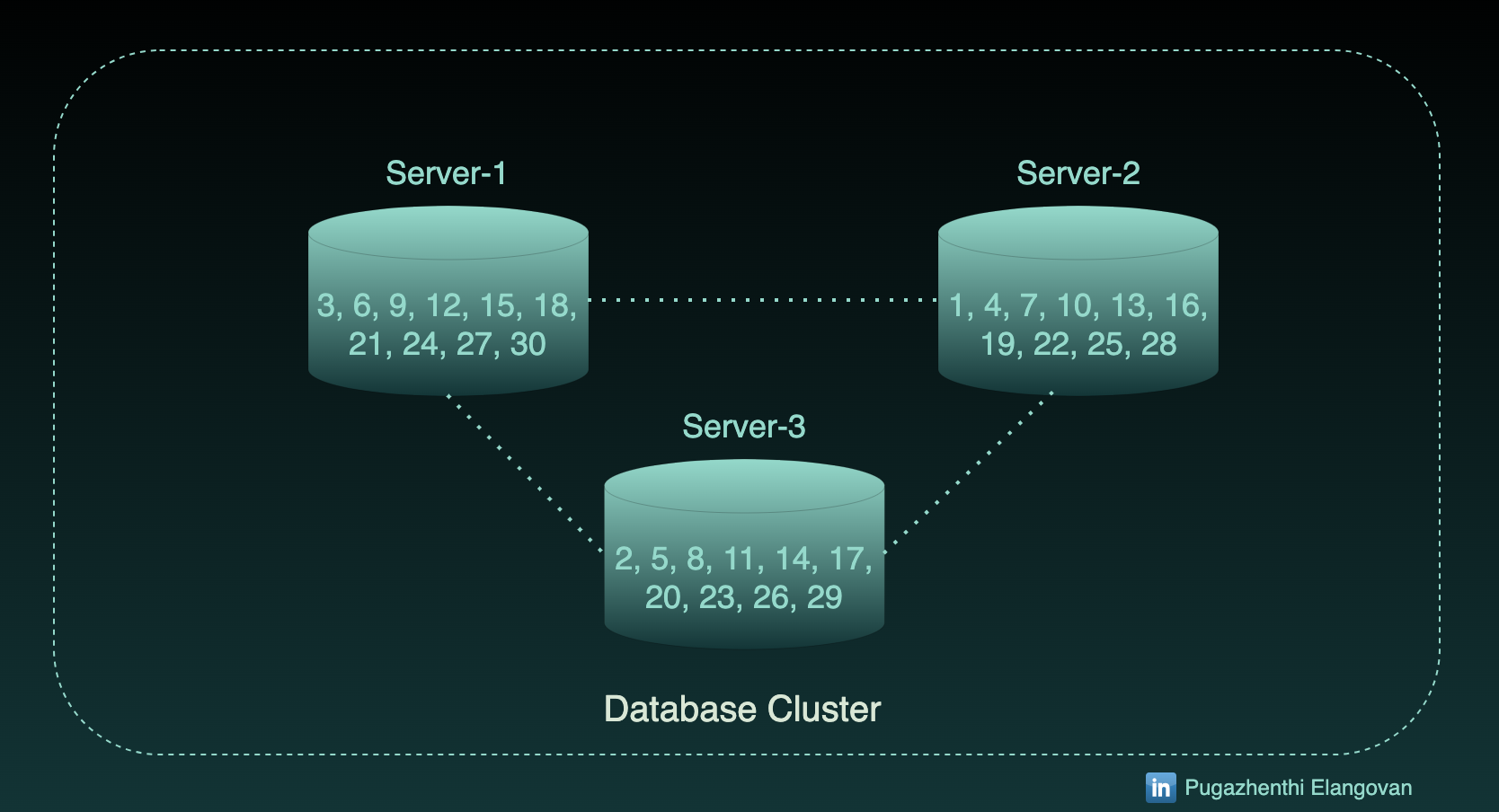
Assume I have 3 servers named 1, 2 and 3, I will go for (Partition key % number of server) + 1 as the hash function to start with.

f(partition_key) % n

It is straightforward. Complexity is O(1).

Say I have the record with partition key 15 to insert, that particular record will go to 1st Server (15 % 3 + 1).

In this manner, let me assign 30 records into the database.

Adding a server

I have to scale out now. Assume, I have added 1 more server.

If the find query is fired for Partition id 15, it will go to Server-3 ((15 % 4) + 1) where the record is not present.

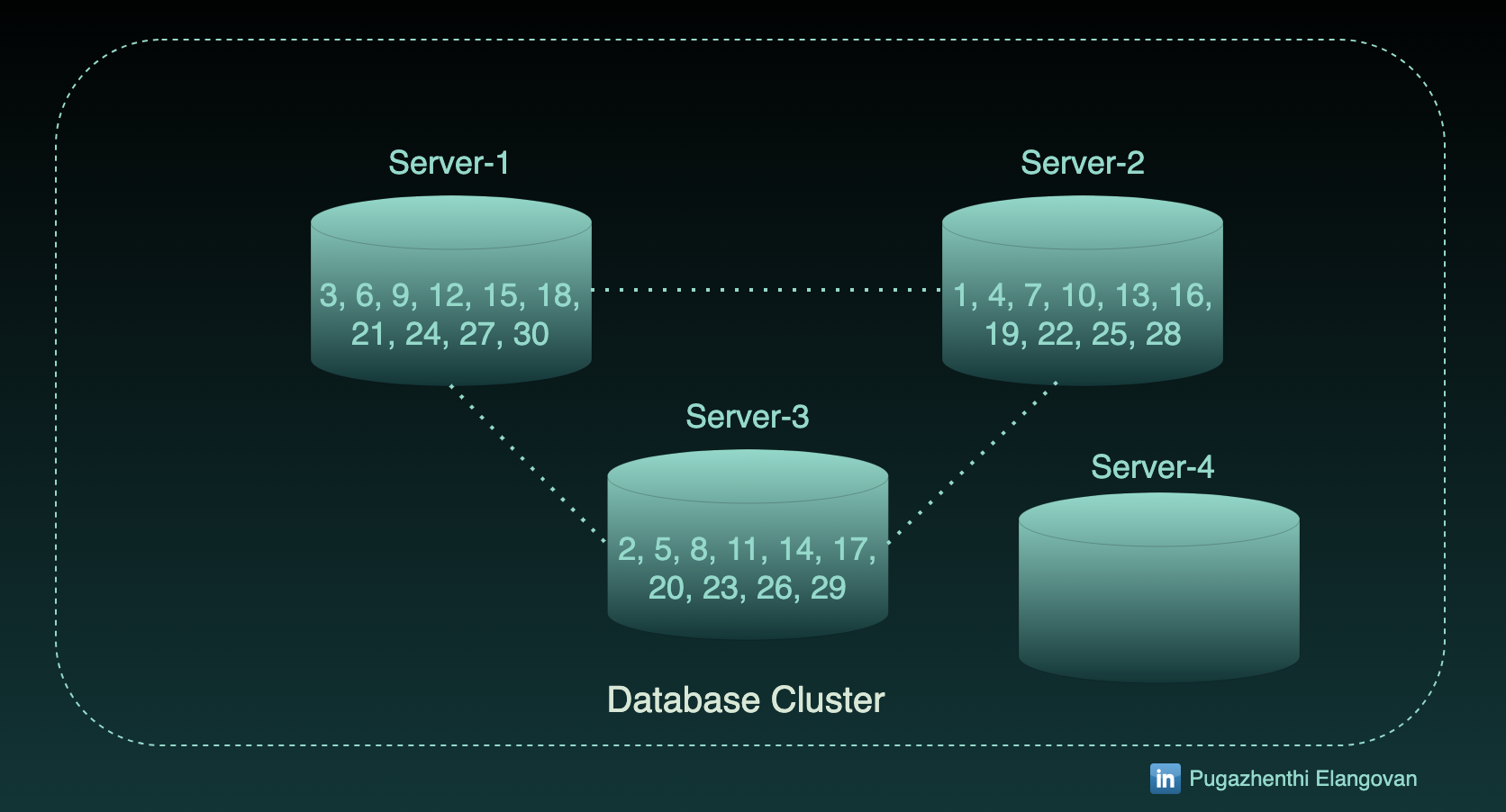
In fact, the Partition 15 resides in Server-1.

At the point where we mark the new server live, 15 has to there in Server-3. Before that point-in-time, Server-1 should be the source for partition 15. This has to happen for all the existing data.

Rehashing existing data

Rehashing is nothing but applying the new server count in the modulo function for all the existing records and to move them appropriately in the Database cluster. It has to happen for every partition for all nodes.

Before marking the new server is ready, I have to replicate the existing records into appropriate servers.

As a result of this, we have to replicate these records into existing servers (Server-1, Server-2 and Server-3) and ingest set of records in Server-4.

Complexity of data movement

Once Server-4 is joined to the cluster and ready to serve data, we can delete the older records in the existing servers.

Most of the existing records across all the existing servers has to be migrated when we introduce new server to the cluster.

• 27 records out of 30 has to be moved across servers.

• Moving 90 % percentage of data in the database for adding a new server it way costly.

• Each server should have larger free storage specific for this data replication during the movement.

• In addition to this data movement, database has to serve live requests of the clients.

• Thus, the load on the cluster can potentially affect the reliability of the database.

Do we need the data movement at all ?

When we introduce the server, it is meant to be share the workload of the existing cluster. There is no point in adding the server if it doesn't share the workload. Thus, It is very obvious that we can't eliminate rehashing and the movement.

Yes, we need to move data. But, How much.?

In the above example, we introduced 7 records in server-4 as you see the image. 30/7 comes around 25 %. 25 percentage of total records has to be moved.

Can we derive it as the proper equation?

The number 7 can be calculated by division of total records / total servers.

Function will be

O(M/N)

where M is the total records and N is the count of the server.

Earlier, It was O(M) - all records.

Now, we can aim to reduce the percentage of data movement which inversely proportional to number of servers. This is just the goal we set to achieve, not the result. Lets solve together.

---

Consistent Hashing

Like all other problems in softwares, Our ancestors found a solution that can minimise the rehashing (or) migration of data when we add the workload.

Lets see it step by step on the same example.

Decouple and conquer

Decoupling the hash output and number of servers.

It removes the dependency of server count in hash function.

Strike down the function using server's count.

(Partition key % number of server)

New function for partition

Derive the hash function to provide the output of pre-determined range of values.

Now the hash function has no parameter which related to the cluster size. Thus, we have to fix the number of partitions we gonna support for the database upfront. It is independent of the volume of data and number of servers.

For example, In cassandra - this hash output range is 2 power -63 to 2 power 63.

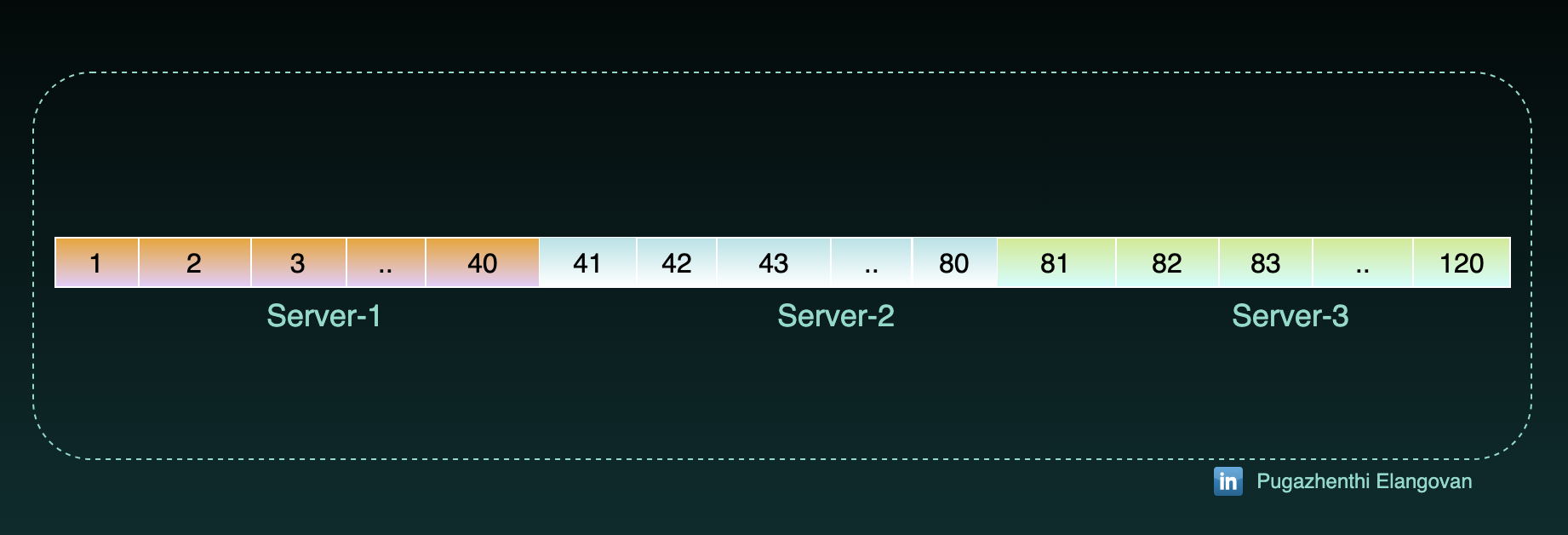
Let's decide we will have 120 partitions. Our hash output will be (1 to 120). Remember 120 is the partition range we fix. Number of servers is still 3.

These pre-determined values are called tokens.

Design:

To arrive at the function to provide only numbers 1 to 120.

Let it be simple as (f(partition_key) % 120) + 1

i.e., f(partition_key) % t where t is the number of tokens. Since it is the constant, function will be

f(partition_key)

Shall we add the record with partition function alone ?

We can't. We need another function for tokens to add the record.

Assign the portion of pre-determined range of values to each server.

Hash output values to servers while setting up the database.

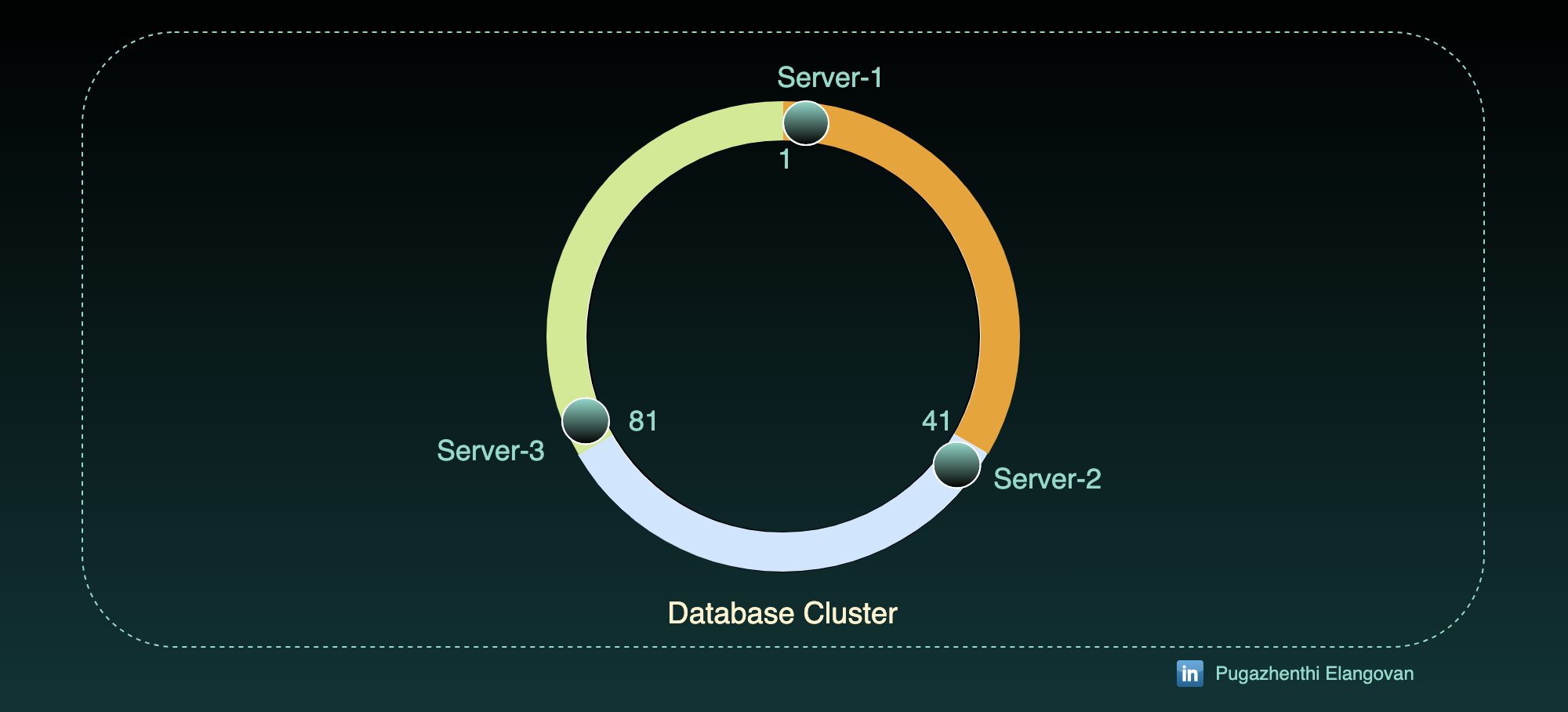
Server-1 : 1 to 40

Server-2 : 41 to 80

Server-3 : 81 to 120

Design:

Actual solution is to fix the tokens and assign server to the token and not vice versa. So,

• We will spread the tokens into ring structure from 0 to 360 degree.

• Assign node to the particular token.

Computation to get the server from token can be the function(token) .

Hence, the overall cost to add/remove an item can be

f(partition) + f(token)

• Complexity of the partition hash function will be O(1) as we seen in earlier case.

Token function

• Token function is dependent on the count of servers. If we map the server to all 120 token, the cost to find the server will be cheap O(1). In real world, token range will so high. The hash range output range is 2 power -63 to 2 power 63.

• So, we will store only the starting number of the range to the server. Thats why we put Server image only on 1, 41 and 81.

• To find the server in the sorted ring of tokens, we have to find the next stop point(angle) where we have mapped the server.

• In short, finding the number in the sorted array. Yes. Binary search has to be performed on the server's data. Complexity of token function is O(log N) where N is the count of the server.

So, the overall complexity will be O(log N) is to add/remove the record.

Great. Shall we assign 30 values like what we done earlier. ?

Set up the existing records (1 to 30) that we seen in earlier examples.

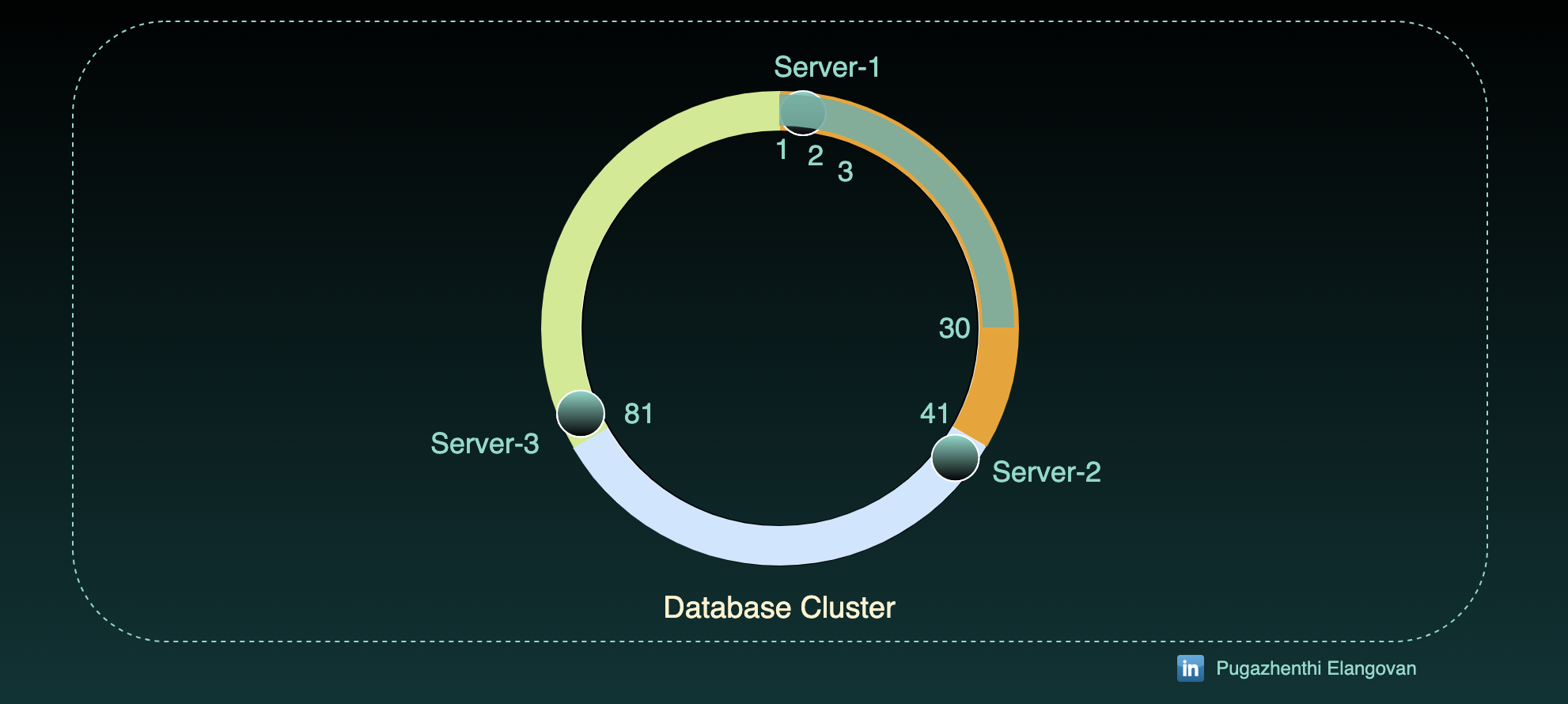
We get the same 1 to 30 the output of partition function x % 120 = x, where 0< x <120.

So, all the 30 records goes into server-1.

Add new node:

Add a new node Server-4 to the existing database cluster at 101.

As result of that,

• Server-4 will take the range of 101 to 120 from Server-3.

Since we didn't have any records in 101-120 tokens, there will be no rearrangement of data.

Let's introduce Server-5 at 21.

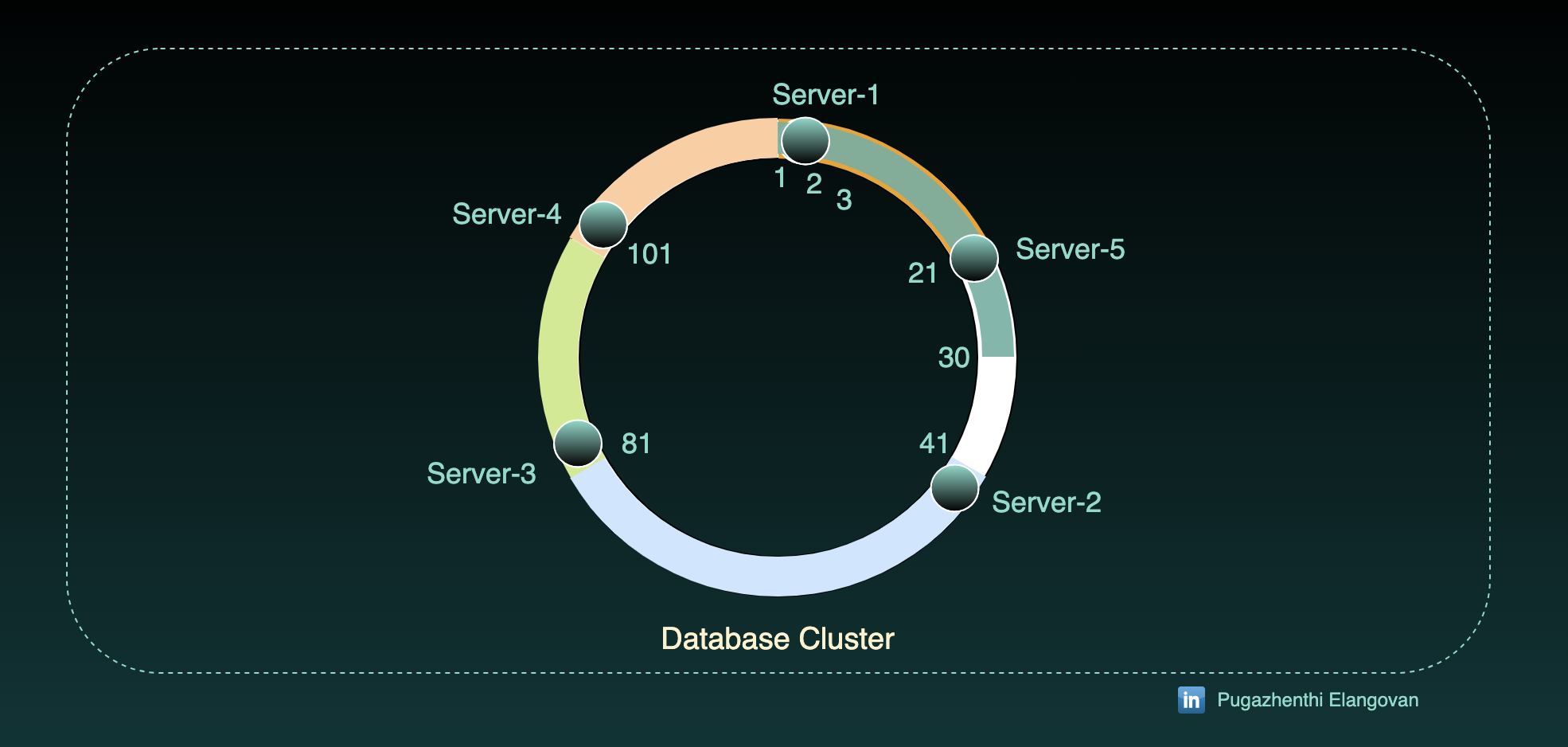
Token starting 21 to 40 will be assigned to Server-5 and so records at 21 to 30 will be moved to Server-5.

Number of records have to be moved will be the order of total tokens / servers count.

Complexity will be number of records to be moved + Complexity of read and write.

O(M/N) + O(log N)

is the complexity to move/re-arrange the data when we add/remove the server.

Conclusion

This decoupling of input data (partition) from the system information (server count) and ring structure token assignment for server mapping together called as consistent hashing. This is being used in almost every distributed system out there.

For the convenience to explain, we haven't talked about the

• Variant of the consistent hashing where we put the same servers in multiple degrees(places) of the ring.

• Ownership of token alignments to servers.

• Ownership of data movement.

• Replication of data.

We will cover the same in upcoming articles.

References

• https://en.wikipedia.org/wiki/Consistent_hashing

• https://www.cs.cornell.edu/projects/ladis2009/papers/lakshman-ladis2009.pdf

• https://www.allthingsdistributed.com/files/amazon-dynamo-sosp2007.pdf

• https://web.stanford.edu/class/cs168/l/l1.pdf

• https://arpitbhayani.me/blogs/consistent-hashing/

Thanks for Reading.

If you liked this post, follow me on LinkedIn.