Essential Guide to Queues: What They Are and How They Work
 Aditya Vaasudev B
Aditya Vaasudev B
Introduction
Whether you're at a railway reservation counter, waiting in line at the movie theater, or submitting print jobs to a network printer, forming a queue is the universal solution to bring order to chaos. By patiently awaiting your turn, you increase the likelihood of receiving better service. Additionally, queues help in maintaining fairness and reducing conflicts among customers. Moreover, queues facilitate a sense of orderliness and civility in public spaces, contributing to a smoother and more pleasant experience for everyone involved.
Applications of queues
Applications of queues as a data structure are even more common than those of stacks. When performing tasks on a computer, it is often necessary to wait your turn before accessing a device or process. Within a computer system, there may be queues of tasks waiting for the printer, disk storage, or CPU in a time-sharing system. Within a single program, there may be multiple requests that need to be kept in a queue, or one task may create other tasks that must be handled in turn by keeping them in a queue.
Queues in Data Structures
Queue is a linear data structure that permits insertion of new element at one end and deletion of an element at the other end. The end at which the deletion of an element take place is called front, and the end at which insertion of a new element can take place is called rear.
Consider a queue of people waiting at a bus stop. Each new person who arrives takes their place at the end of the line, and when the bus comes, the people at the front of the line board first. The first person in the line is the first person to leave.
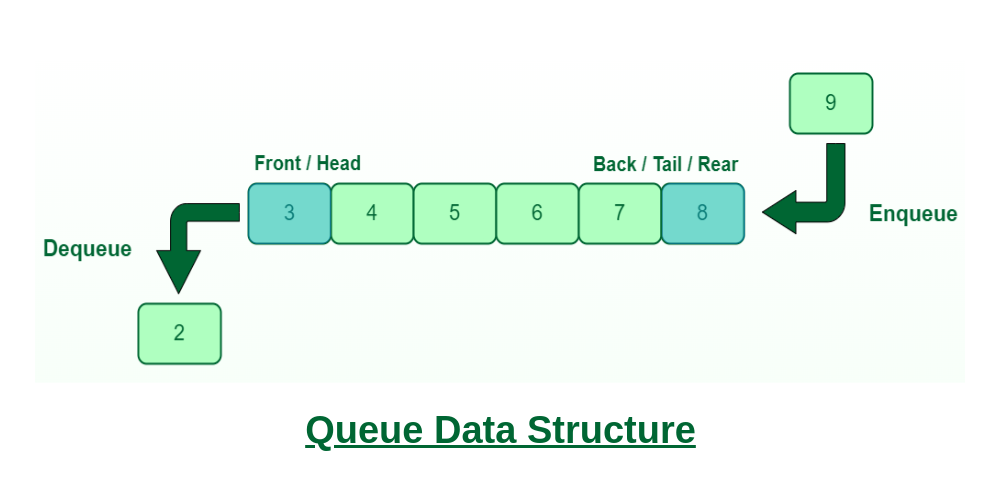
The deletion or insertion of elements can take place only at the front or rear end of the list respectively.
The first element that gets added into the queue is the first one to get removed from the list.
Hence, a queue is also referred to as a first-in-first-out (FIFO) list.
Operations on queue
| Operation | Description |
| enqueue | used for inserting an element to the rear of the queue |
| dequeue | used to remove and return the element at the front of the queue |
| peek | it returns the element at the front of the queue without removing it |
| isEmpty() | it checks if the queue is empty |
| isFull() | it checks if the queue is full |
Enqueue() :
If the queue is full, it prints an error message.
Otherwise, it increments the
rearindex and adds the value to thequeuearray.If the queue was empty before adding the value, the
frontindex is set to 0.
void enqueue(int value)
{
if (isFull())
printf("\nQueue is Full!!");
else
{
if (front == -1)
front = 0;
rear++;
queue[rear] = value;
printf("Inserted -> %d", value);
}
}
Dequeue() :
If the queue is empty, it prints an error message.
Otherwise, it prints the value at the
frontindex and increments thefrontindex.If the
frontindex becomes greater than therearindex after removing an element, both indices are set to -1 to indicate that the queue is empty.
void dequeue()
{
if (isEmpty())
printf("\nQueue is empty!!");
else
{
printf("Deleted value = %d", queue[front]);
front++;
if (front > rear)
{
front = rear = -1;
}
}
}
Peek() :
This function prints the front element of the queue without removing it.
If the queue is empty, it prints an error message.
void peek()
{
if (isEmpty())
printf("Queue is empty");
else
printf("Front element is %d", queue[front]);
}
isEmpty() :
This function checks if the queue is empty by comparing the
frontandrearindices.If they are equal, the queue is empty and the function returns 1.
Otherwise, it returns 0.
int isEmpty()
{
if (front == rear)
return 1;
else
return 0;
}
isFull() :
This function checks if the queue is full by comparing the
rearindex with the maximum size of the queue.If they are equal, the queue is full and the function returns 1.
Otherwise, it returns 0.
int isFull()
{
if (rear == MAX - 1)
return 1;
else
return 0;
}
Code
#include <stdio.h>
#define MAX 5
int queue[MAX];
int front = -1;
int rear = -1;
int isEmpty()
{
if (front == rear)
return 1;
else
return 0;
}
int isFull()
{
if (rear == MAX - 1)
return 1;
else
return 0;
}
void enqueue(int value)
{
if (isFull())
printf("\nQueue is Full!!\n");
else
{
if (front == -1)
front = 0;
rear++;
queue[rear] = value;
printf("Inserted -> %d\n", value);
}
}
void dequeue()
{
if (isEmpty())
printf("\nQueue is empty!!\n");
else
{
printf("Deleted value = %d\n", queue[front]);
front++;
if (front > rear)
{
front = rear = -1;
}
}
}
void peek()
{
if (isEmpty())
printf("Queue is empty");
else
printf("Front element is %d\n", queue[front]);
}
void display() {
if(isEmpty()) {
printf("Queue is Empty!!!");
} else {
printf("\nQueue elements are: ");
for (int i = front; i <= rear; i++) {
printf("%d ", queue[i]);
}
}
printf("\n");
}
int main()
{
dequeue(); // Queue is empty!!
enqueue(1); // Inserted -> 1
enqueue(2); // Inserted -> 2
enqueue(3); // Inserted -> 3
enqueue(4); // Inserted -> 4
enqueue(5); // Inserted -> 5
enqueue(6); // Queue is Full!!
peek(); // Front element is 1
display(); // Queue elements are: 1 2 3 4 5
dequeue(); // Deleted value = 1
dequeue(); // Deleted value = 2
dequeue(); // Deleted value = 3
display(); // Queue elements are: 4 5
return 0;
}
Thank you! I am glad you made it to the end of this article. I hope you got to learn something :)
Subscribe to my newsletter
Read articles from Aditya Vaasudev B directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
