the problem with skewed datasets

A skewed dataset is a dataset where the outputs are not evenly split. In other words, if our dataset has 10 training examples, 8 of them have an expected output y-hat of 1 whereas only 2 of them have an expected output of 0. In this case, the error metrics we’ve discussed before, such as the fraction of the dataset that was misclassified, may not be a good indicator of the performance of the model. Thus, we need to use a different metric to gauge the model’s accuracy.

A popular pair of error metrics used in this situation is called precision/recall. We must first start by creating a confusion matrix, which looks like the following:

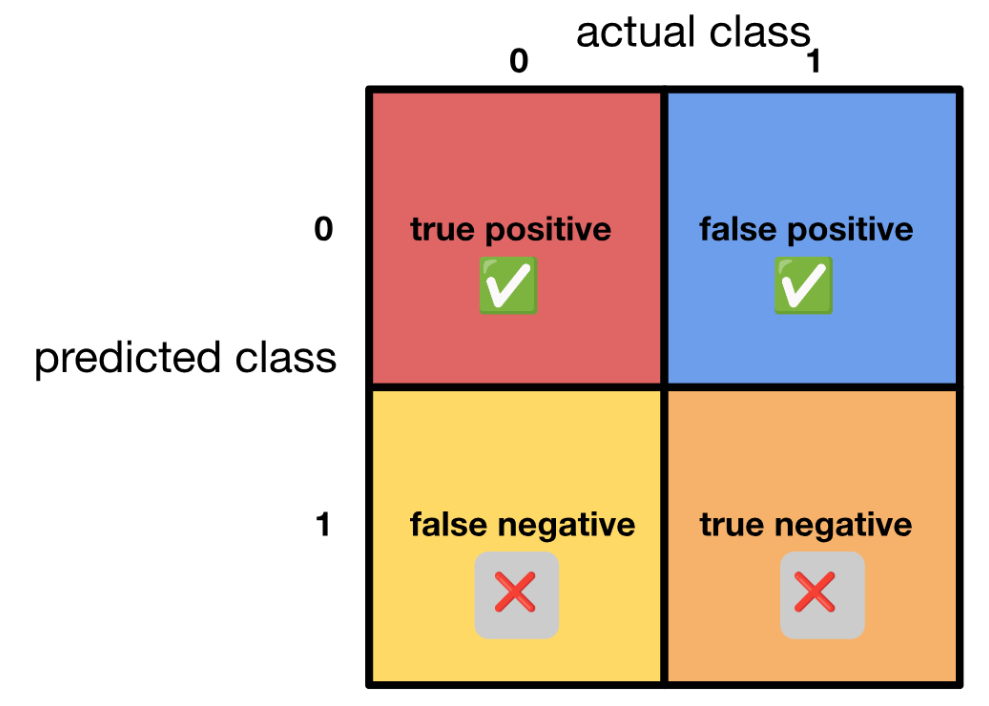
Given the above confusion matrix, if y = 1 is the presence of a rare class we want to be able to detect with our model,

precision = # true positives/# predicted positives

i.e.,

precision = # true positives/(# true positives + # false positives)

Precision is the fraction of the predicted positives that were correct.

Furthermore,

recall = # true positives/# actual positives

i.e.,

precision = # true positives/(# true positives + # false negatives)

Recall is the fraction of the actual positives that were predicted correctly.

If either precision or recall are very low, it is an indicator that your model is not useful. Ideally, we would want our model to have both high precision and high recall. However, in most cases, there will be a tradeoff between precision and recall.

(1) If you want higher precision, you can raise the threshold (decision boundary) that decides whether the output will be 1 or 0. For example, earlier when we were discussing logistic regression, we set the threshold to 0.5, saying that anything above or equal to 0.5 will be classified as 1 and anything under will be classified as 0. If we increase this threshold to say, 0.7, we increase precision because when the model classifies something as 1, we are more sure that it is 1. So, in other words, when the model yields a positive, it is more likely to actually be a positive. However, this increased precision comes at the cost of recall because now we are also leaving out the cases where we weren’t as sure that the example was a 1, so we automatically misclassified it as a 0 (in other words, the number of false negatives increases). This decreases the recall value.

(2) If you want higher recall, lower the threshold. This has the opposite effect of increasing recall at the cost of precision (there will be more false positives). The number of positives predicted will increase overall, but not all of those positive predictions will be correct (some of them should actually be negative).

Which path to take depends on the context and what the neural network is going to be used for. If our neural network is being used to determine which strawberries are rotten vs. fresh, it is probably not a huge problem if we have a couple of false negatives occur; as long as the strawberry is not immensely rotten (which the neural network will detect since the confidence level will be high), we can generally ignore the false negatives since they won’t have too much of a bad impact. However, if our neural network is being used for cancer detection, for example, false negatives are orders of magnitude more dangerous than false positives, which can be later corrected by doctors. Thus, in this case, lowering the threshold may be a wiser decision.

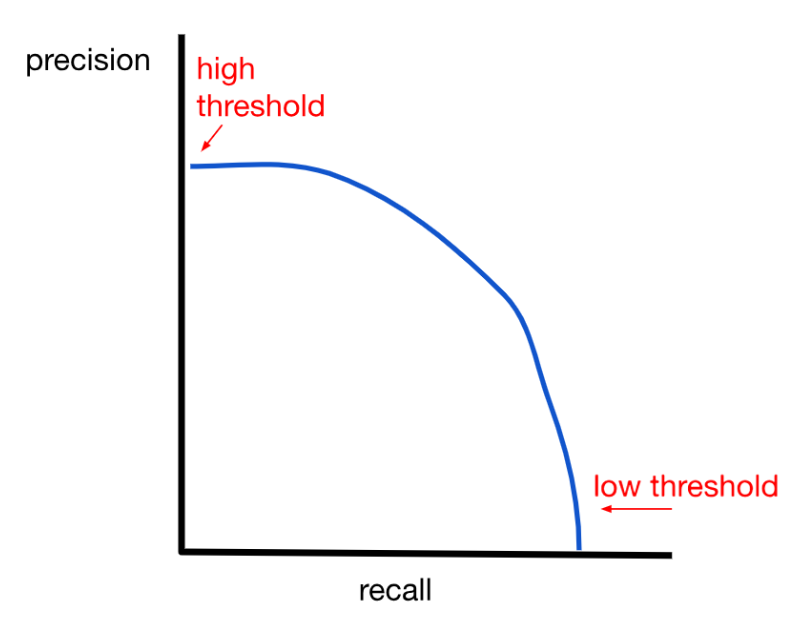
To pick the best trade-off between precision and recall, we can use another metric called the F1 score. The F1 score is useful because it combines the precision and recall scores into one number, allowing us to better compare different models against each other.

F1 score = 2(precision*recall)/(precision + recall)

The higher the F1 score, the better the model. Note that this above equation is also known as the harmonic mean of precision (P) and recall (R).