Stack Data Structure
 Back2Lobby
Back2LobbyWe covered array and linked lists in previous articles. Now we got a much simpler data structure "Stack". It represents a simple LIFO (The last-in, first-out) list which only allows you to extract/read items one by one starting from the last inserted item. So, in order to read the last item (inserted first), you have to pull out all the items.
Real world use case of this data structure could be a video game where some books are placed on top of each other. Which allows only extracting one item (top one) at a time. Even though other data structures can be used but one can also use stack which is a much simpler and perfect for this use case.
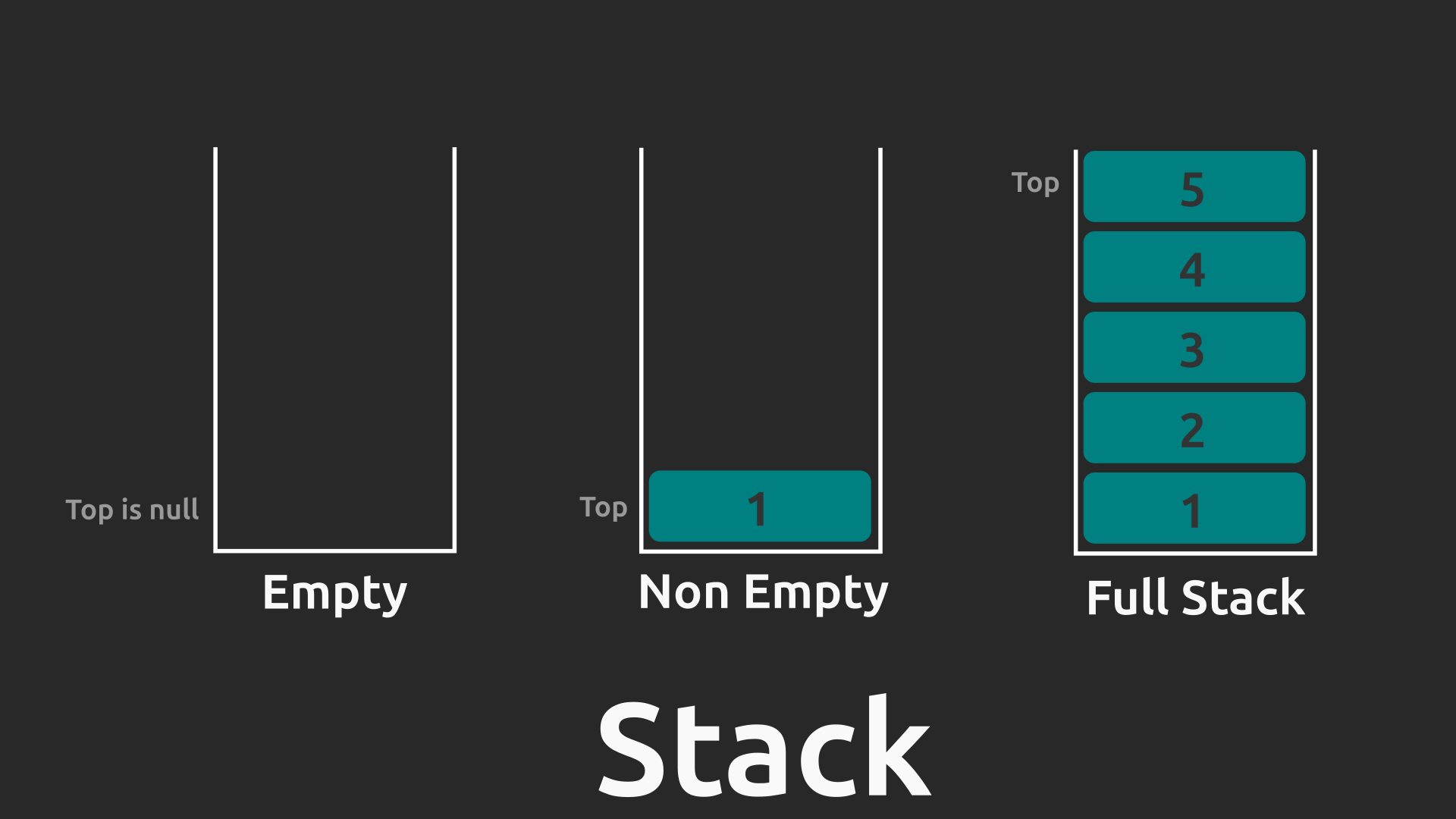
This stack implementation allows limited capacity for storing items for learning purposes also because of the way C++ works. But for a stack with dynamic capacity, one can use linked list based stack implementation. However, we will go through array based implementation.
Let's start our implementation by defining a struct for the stack.
const int MAX_SIZE = 3;
struct Stack {
private:
int top = -1;
int items[MAX_SIZE];
}
Alright, so we got a Stack struct which contains an array items of specified size. We have another property top which contains the index of top item. Where -1 indicates its empty and pointing to nothing.
Talking about the implementation of the struct methods, we need basic operations like push, pop, peek for our stack. Starting with push method:
void push(int value) {
if (isFull()) {
cout << "\n STACK FULL \n";
return;
}
items[top + 1] = value;
top++;
}
It’s simply checking if there is space for another item in the stack or not. If yes, add it in the items array and increase the index pointed in the top property. While isFull is simply a utility method which checks stack capacity based on items array size and top index.
bool isFull() { return top == MAX_SIZE - 1; }
Implementation of pop method is pretty similar too.
void pop() {
if (isEmpty()) {
cout << "\n STACK IS EMPTY \n";
return;
} else {
top--;
}
}
We are simply changing the index stored in top. One little drawback I see with this approach is the popped item in the array stays there on popping until the next item is pushed. When we pop an item it simply changes the top index of stack but the item stays in the items array. But when we push another item after that, it overwrites at that unnecessary item.
The isEmpty method here is another utility method used to determine if stack is empty.
bool isEmpty() { return top <= -1; }
Now, we can push and pop but we need a method to get the item at top of stack. Here we go:
int peek() {
if (isEmpty()) {
cout << "\n STACK IS EMPTY \n";
return 0;
} else {
return items[top];
}
}
This method returns if there is an item in the stack otherwise simply return 0 with a message saying that the stack is empty.
Here is full code along with tests.
// ignore/remove the 2 lines below if you don't want any tests
#define DOCTEST_CONFIG_IMPLEMENT_WITH_MAIN
#include "doctest.h"
using namespace std;
const int MAX_SIZE = 3;
struct Stack {
private:
int top = -1;
int items[MAX_SIZE];
public:
void push(int value) {
if (isFull()) {
cout << "\n STACK FULL \n";
return;
}
items[top + 1] = value;
top++;
}
void pop() {
if (isEmpty()) {
cout << "\n STACK IS EMPTY \n";
return;
} else {
top--;
}
}
int peek() {
if (isEmpty()) {
cout << "\n STACK IS EMPTY \n";
return 0;
} else {
return items[top];
}
}
bool isEmpty() { return top <= -1; }
bool isFull() { return top == MAX_SIZE - 1; }
};
// TESTS
TEST_CASE("push method works correctly") {
Stack *stack = new Stack();
stack->push(34);
CHECK(stack->peek() == 34);
stack->push(25);
CHECK(stack->peek() == 25);
}
TEST_CASE("pop method works correctly") {
Stack *stack = new Stack();
stack->push(34);
stack->push(25);
stack->pop();
CHECK(stack->peek() == 34);
}
Time Complexity
All the operations including push, pop and peek in stack have time complexity of O(1) because it's a straightforward process there are no loops involved. No matter how big the stack gets, we can always say that these operations will take constant time.
Subscribe to my newsletter
Read articles from Back2Lobby directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
