Essential Math & Concepts for LLM Inference
 Venkat Raman
Venkat Raman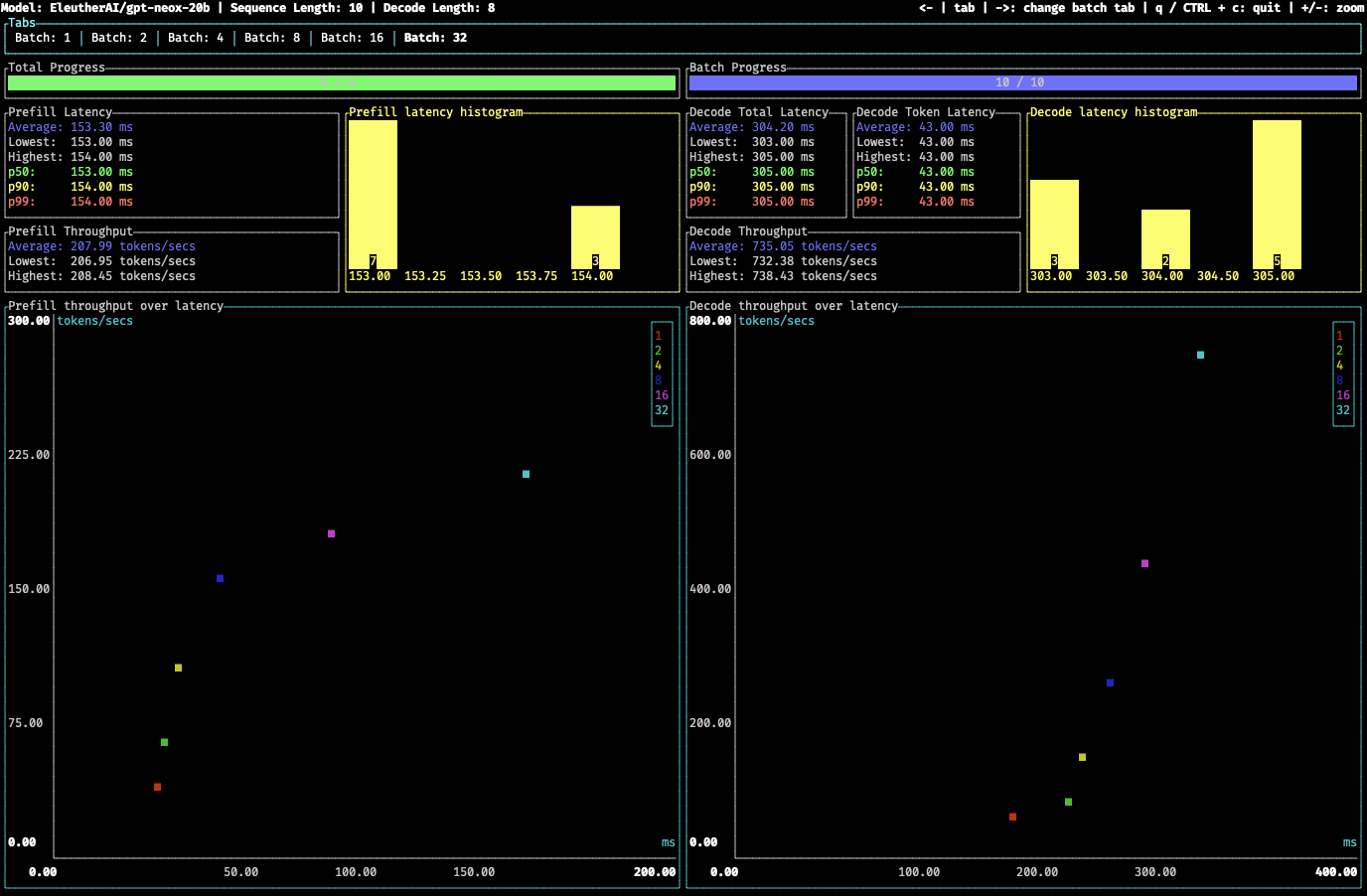
(Image Credit: HF TGI Benchmark)
Introduction
As enterprises and tech enthusiasts increasingly integrate LLM applications into their daily workflows, the demand for TFLOPS is ever increasing. Apple, Microsoft, Google, and Samsung have already introduced products that boast formidable TFLOPs dedicated to powering LLMs. LLMs have rapidly become more than tools; they serve as digital companions, akin to a digital intern or a 'rubber duck' for problem-solving. As we move forward, we’ll see an increase in both local and cloud-based LLMs. In contrast to the unfulfilled promises of Web3, LLMs are emerging as the real deal, bringing tangible advancements and utilities.
The LLM inference tasks require a lot of computing power and work in parallel, pushing modern GPUs to their limits. I see this being similar to early days of computing via time-sharing. Although techniques such as Paged Attention optimize LLM inference by mirroring the functionality of modern CPU MMUs, there are several hardware and model optimizations still needed. From my own experience over the last 2.5 years, the pace of progress in research related to LLM training and inference optimization is truly remarkable, with breakthroughs emerging every six months. I think these are the essential math & concepts for engineers working in LLM inference space as we are stepping into this new era.
The Essentials
Last Updated: 2024-05-31
Number of parameters in a GPT-style model
P ~= 12 * n_layers * d_model^2
n_layers - No of layers in the neural network
d_model - Dimensionality of the embeddings or the size of the hidden layers within the model
12 - Architecture specific average parameter count across sub-layers excluding attention heads
## Llama 7B - n_layers = 32 - d_model = 4096 P ≈ 12 * n_layers * d_model^2 P ≈ 12 * 32 * 4096^2 P ≈ 6442450944 ≈ 6.44 billion parameters ## Llama 13B - n_layers = 40 - d_model = 5120 P ≈ 12 * n_layers * d_model^2 P ≈ 12 * 40 * 5120^2 P ≈ 12537472000 ≈ 12.54 billion parameters
Model data types
| Data Type | Bytes per Parameter |
|-----------|----------------------|
| FP32 | 4 bytes |
| FP16 | 2 bytes |
| BF16 | 2 bytes |
| INT8 | 1 byte |
| INT4 | 0.5 bytes |
GPU Memory requirements
Model weights
Model weights memory (bytes) ~= P * p_a
P - No of model parameters
p_a - No of bytes per parameter
# Llama 2 - FP16
## Llama 7B
Memory (bytes) ≈ 7 * 10^9 * 2 ≈ 14 billion
≈ 14 billion bytes / 10^9 ≈ 14 GB
## Llama 13B
Memory (bytes) ≈ 13 * 10^9 * 2 ≈ 26 billion
≈ 26 billion bytes / 10^9 ≈ 26 GB
# Llama.cpp - INT4
## Llama.cpp 7B
Memory (bytes) ≈ 7 * 10^9 * 0.5 ≈ 3.5 billion
≈ 3.5 billion bytes / 10^9 ≈ 3.5 GB
## Llama.cpp 13B
Memory (bytes) ≈ 13 * 10^9 * 0.5 ≈ 6.5 billion
≈ 6.5 billion bytes / 10^9 ≈ 6.5 GB
KV cache
Here are some excellent resources to understand details about KV cache:
KV cache memory (bytes) ~= B * (2 * n_layers * n_heads * d_head * t_seq_len * p_a)
B - Batch size (No of sequences processed simultaneously). Essential for efficient compute and memory utilization, throughput, latency and time to first token
2 - For both K & V caches
n_layers - No of layers in the neural network, kv cache is per layer
n_heads - No of attention heads per layer
d_head - Dimension of each attention head
t_seq_len - total sequence length (No of input and output tokens)
p_a - No of bytes per parameter
# Llama 2 - FP16, B=1, t_seq_len=2048
## Llama 7B - n_layers = 32, n_heads = 32, d_head = 128 (4096 / 32)
Memory (bytes) ≈ 1 * (2 * 32 * 32 * 128 * 2048 * 2)
≈ 1,073,741,824 bytes
≈ 1.07 billion
≈ 1.07 billion bytes / 10^9 ≈ 1.07 GB
## Llama 13B - n_layers = 40, n_heads = 40, d_head = 128 (5120 / 40)
Memory (bytes) ≈ 1 * (2 * 40 * 40 * 128 * 2048 * 2)
≈ 1,342,177,280 bytes
≈ 1.34 billion
≈ 1.34 billion bytes / 10^9 ≈ 1.34 GB
# Llama.cpp - INT4, B=1, t_seq_len=2048
## Llama.cpp 7B - n_layers = 32, n_heads = 32, d_head = 128 (4096 / 32)
Memory (bytes) ≈ 1 * (2 * 32 * 32 * 128 * 2048 * 0.5)
≈ 268,435,456 bytes
≈ 268 million
≈ 0.27 billion bytes / 10^9 ≈ 0.27 GB
## Llama.cpp 13B - n_layers = 40, n_heads = 40, d_head = 128 (5120 / 40)
Memory (bytes) ≈ 1 * (2 * 40 * 40 * 128 * 2048 * 0.5)
≈ 335,544,320 bytes
≈ 336 million
≈ 0.34 billion bytes / 10^9 ≈ 0.34 GB
Activation
Activation memory refers to the memory required to store intermediate activations or outputs during the forward and backward passes of a neural network.
Activation memory (bytes) ~= B * t_seq_len * E * C
B - Batch size
t_seq_len - total sequence length (No of input and output tokens)
E - embedding dimension or hidden size of the model
C - Constant factor that depends on the specific model architecture and implementation details
# Llama 2, Llama.cpp - 7 & 13 B; B=1, t_seq_len=2048
Memory (GB) ≈ 0.3 & 0.5 GB
Total
Total Memory (bytes) = Model weights + KV cache + Activation + Overhead
- Overhead - Platform or framework specific overhead
Model weights and kv cache account for ~90% of total GPU memory requirements during inference.
Memory per Token
For quick back of the envelope calculations, calculating - memory for kv cache, activation & overhead is an overkill. I find this more useful:
Total Memory (bytes) ~= Model weights + (No of Tokens * Memory per Token)
No of Tokens - Batch size * total sequence length
Memory per Token - A constant (~1MB for a 13B model)
Metrics
Latency
s/token
lower latency means quick & efficient processing
optimizing this means better user experience, but not necessarily maximizing resource utilization
Throughput
queries/s or tokens/s
adjusting batch size affects throughput
higher throughput means maximizing memory bandwidth utilization & MFU (model FLOPS utilization)
higher throughput also means slightly higher latency when compared to B=1
works well for offline batch requests as increased latency is tolerable while processing several queries at a time by increasing batch size
have to find a balance between min latency and max utilization for online requests and this ideal batch size for max seq length must be identified
Time to first token
Since generation tasks result in 100s or even thousands of tokens, users waiting until generation is complete is not a good experience
lower value means improved user experience
Response streaming enables reduced time to first token
Generation involves prefill + decode phase.
During prefill, kv cache is ready with input tokens and the first output token is generated
During decode, subsequent completion tokens are generated
Since TTFT decreases overall query latency significantly, batch size can be increased even in online inference requests thus increasing GPU utilization & also improving user experience
Utilization
In NVIDIA A10 GPU:
24GB GDDR6 HBM of bandwidth 600GB/s
Peak 125 FP16 TFLOP/s by Tensor Cores
Peak FLOP per Byte for MatMul = peak FP16 FLOP per sec / bandwidth in bytes per sec = 208
In NVIDIA A100 SXM GPU:
80GB HBM2e of bandwidth 2.39 TB/s
Peak 312 FP16 TFLOP/s by Tensor Cores
Peak FLOP per Byte for MatMul = peak FP16 FLOP per sec / bandwidth in bytes per sec = 130
# A10
Bandwidth = 600 * 10^9 bytes/second
Peak FP16 FLOP/s = 125 * 10^12 FLOP/s
Peak FLOP per Byte = (125 * 10^12 FLOP/s) / (600 * 10^9 bytes/s)
= (125 / 600) * 10^3
= 208.33
# A100
Bandwidth = 2.39 * 10^12 bytes/second
Peak FP16 FLOP/s = 312 * 10^12 FLOP/s
Peak FLOP per Byte = (312 * 10^12 FLOP/s) / (2.39 * 10^12 bytes/s)
= (312 / 2.39)
= 130.54
It means for every byte of date moved, 208 FLOP operations must happen to achieve peak processing. If not, the model / algorithm running on A10 is spending more time moving data rather than on computations. i.e., memory bandwidth bound
Also notice the next generation A100, with very high HBM, FLOP/Byte is significantly lower thus improving model performance
From kipply's excellent transformer arithmetic article, we know that it takes 2*P FLOPS to generate a single token during inference
Total model memory ~= model weights + kv cache size
Let's take Llama 7B FP16 as an example.
# A10 - Llama 7B Total FLOPs & Inference time
## Llama 2 7B - FP16, B=1, t_seq_len=2048
Total FLOPS ≈ 2 * 7 * 10^9 * 1 * 2048
≈ 14 * 2048 * 10^9 FLOPS
≈ 28.672 * 10^12 FLOPS
A10 Inference time ≈ (28.672 * 10^12) / (125 * 10^12 per sec)
≈ 0.229 seconds
-------------------------------------------------------------------
## Llama 2 7B - FP16, B=8, t_seq_len=2048
Total FLOPS ≈ 2 * 7 * 10^9 * 8 * 2048
≈ 14 * 2048 * 8 * 10^9 FLOPS
≈ 229.376 * 10^12 FLOPS
A10 Inference time ≈ (229.376 * 10^12) / (125 * 10^12)
≈ 1.835 seconds
-------------------------------------------------------------------
## Llama 7B - FP16, B=1, t_seq_len=4096
Total FLOPS ≈ 2 * 7 * 10^9 * 1 * 4096
≈ 14 * 4096 * 10^9 FLOPS
≈ 57.344 * 10^12 FLOPS
A10 Inference time ≈ (57.344 * 10^12) / (125 * 10^12)
≈ 0.4587 seconds
-------------------------------------------------------------------
## Llama 7B - FP16, B=4, t_seq_len=4096
Total FLOPS ≈ 2 * 7 * 10^9 * 4 * 4096
≈ 14 * 4096 * 4 * 10^9 FLOPS
≈ 229.376 * 10^12 FLOPS
A10 Inference time ≈ (229.376 * 10^12) / (125 * 10^12)
≈ 1.835 seconds
The above calculations show that increase in batch size and/or total_seq_len linearly increases FLOPS. This will affect inference latency. So finding ideal batch size for t_seq_len as per underlying hardware is important. This is also evident in HF TGI's awesome benchmark tool.
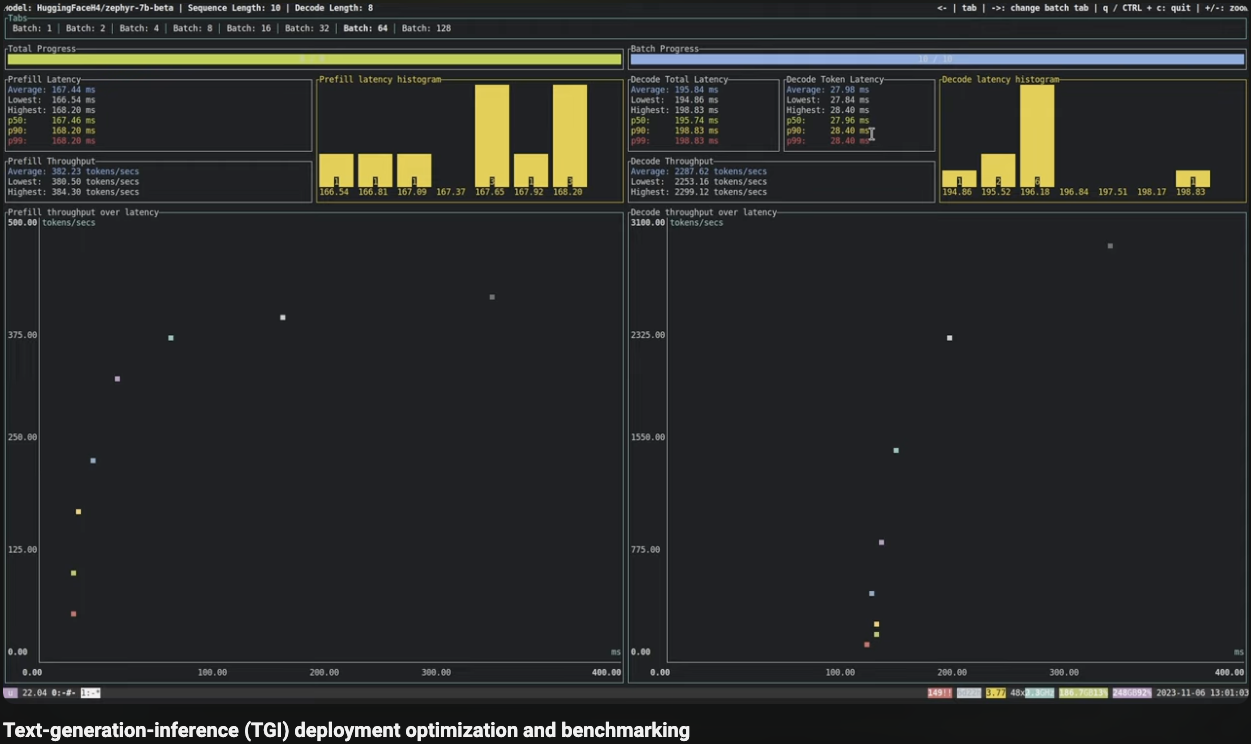
(Image Credit: HF TGI Benchmark)
From baseten's excellent transformer inference article
# Total memory movement during a standard single headed attention calculation
total_memory_movement_in_bytes = 8N^2 + 8Nd bytes
N - is the sequence length of the LLM,
d is the dimension of a single attention head.
Total memory movement in decode phase
≈ n_layers * n_heads * (8N^2 + 8Nd bytes)
# Total FLOPS during a standard single headed attention calculation
total_compute_in_floating_point_ops = 4(N^2)d + 3N^2 FLOPS
Total FLOPS during decode phase
≈ n_layers * n_heads * 4(N^2)d + 3N^2 FLOPS
# A10 - Llama 7B Memory, arithmetic intensity & data movement
## Llama 2 7B - FP16, B=1, t_seq_len=2048, n_layers=32, n_heads=32
Total model memory ≈ model weights + kv cache size
≈ 14 GB + 1.07 GB ≈ 15.07 GB
-----------------------------------------------------------------------
Arithmetic intensity of standard single headed attention:
Memory movement (Bytes) = 8N^2 + 8Nd bytes
= 8 × (2048^2) + 8 × 2048 × 128
= 8 × 4194304 + 8 × 2048 × 128
= 33554432 + 2097152
= 35651584 bytes
≈ 35.65 MB
FLOPS = 4(N^2)d + 3N^2
= 4 × 128 × 4194304 + 3 × 4194304
= 2147483648 + 12582912
= 2159066560 operations
≈ 2159 MFLOPS (Mega Flops)
Peak FLOP per Byte for
Llama2 single headed attention
= peak FP16 FLOP per sec / bandwidth in bytes per sec = 208
= 2159 MFLOPS / 35.65 MB
≈ 60
------------------------------------------------------------------------
Memory data movement time
≈ ((Prefill + Decode + Output) data movement ) / bandwidth
≈ ((14 GB + (32 * 32 * 35.65 MB)+ 1.07 GB)) / 600 GB/s
≈ ((14 GB + 1283 GB + 1 GB)) / 600 GB/s
≈ 2.16 seconds
(n_head, n_layer calculations happen in parallel)
From above calculations, we can see that:
decode phase dominates FLOPS and data movement time.
Peak FLOP/Byte of Llama2 single headed attention calculation 60 is significantly lesser than Peak FLOP/Byte for MatMul 208 the theoretical peak for A10
# Batch size to fully utilize memory bandwidth of 600GB/s
## For t_seq_len=2048
B ≈ 548 (i.e., 14 GB + (548 * 1.07 GB) ≈ 600.36 GB)
## For t_seq_len=4096
B ≈ 273 (i.e., 14 GB + (273 * 2.14 GB) ≈ 600 GB)
These are not possible because available HBM is 24GB and reading from slower storage (SSD) will result in high compute intensity. We saw that the max possible batch sizes are 8 and 4 respectively for t_seq_len of 2048 & 4096.

Side note: Model inference algorithmic complexity is high in prefill phase and is low in decode phase. Most of the time in LLM inference is spent in decode phase (generation). NVIDIA H200 hardware is more optimized for this.
Insights from Model Latency & Understanding Hardware Utilization on Modern GPUs
latency_model = max(latency_compute, latency_memory)
Since decode phase dominates FLOPS & HBM bandwidth, transformer inference is almost always bandwidth limited (memory bound). i.e., compute is underutilized. Increasing batch size will improve this. With significantly large enough batch size, we can get to compute bound regime. But such large batch sizes are not practical.
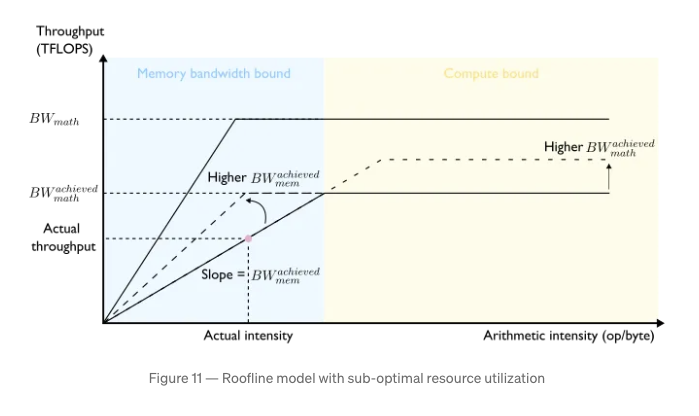
Improvements in model algorithms like Flash Attention result in efficient memory bandwidth utilization and also FLOPS utilization.
(Image credit: Pierre Lienhart's LLM Inference Series: 5. Dissecting model performance)
Outro
Prior to getting into level details of Transformer Inference, my assumption was model architecture, implementation algorithm, etc., are all well optimized. It's not the case and there is significant research and improvement being done here (Flash Attention, Paged Attention, Quantization, GQA, SWA, Continuous batching, etc.,). If we think about it, CPUs have been optimized for several decades for general purpose compute.
NVIDIA GPUs were designed for graphics processing with simple instruction set and not for Transformer processing. Now because of the success of LLMs, NVIDIA GPU hardware design is being optimized for Transformer processing. Apple's M3 & M4 NPU chips have hardware level MMU capabilities (Dynamic Caching). NVIDIA A100 doesn't have this and that's why PagedAttention (similar to how OS paging works with CPU MMU) had to be implemented.
References
LLAMA 2 7B model weight tensor shapes https://blog.gopenai.com/what-are-the-llama-model-weights-e83a58cef1be
GPU Poor Calculator https://github.com/RahulSChand/gpu_poor/tree/main
Efficiently Scaling Transformer Inference https://arxiv.org/pdf/2211.05102
https://www.baseten.co/blog/llm-transformer-inference-guide/
https://www.baseten.co/blog/nvidia-a10-vs-a10g-for-ml-model-inference/
https://medium.com/@plienhar/llm-inference-series-3-kv-caching-unveiled-048152e461c8
https://medium.com/@plienhar/llm-inference-series-4-kv-caching-a-deeper-look-4ba9a77746c8
https://medium.com/@plienhar/llm-inference-series-5-dissecting-model-performance-6144aa93168f
Mistral CTO on LLM Inference- https://youtu.be/mYRqvB1_gRk?si=xugY8qU5_FQLlN58
https://www.anyscale.com/blog/continuous-batching-llm-inference
NVIDIA A10 - https://www.nvidia.com/content/dam/en-zz/Solutions/Data-Center/a10/pdf/a10-datasheet.pdf
NVIDIA A100 - https://www.nvidia.com/content/dam/en-zz/Solutions/Data-Center/a100/pdf/nvidia-a100-datasheet-us-nvidia-1758950-r4-web.pdf
HF TGI benchmark graph - https://youtu.be/jlMAX2Oaht0?si=xpBm8YgkXeiT7t6E
https://www.semianalysis.com/p/nvidia-blackwell-perf-tco-analysis
https://www.semianalysis.com/p/on-device-ai-double-edged-sword
Subscribe to my newsletter
Read articles from Venkat Raman directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Venkat Raman
Venkat Raman
🧑💻 Staff Engineer – Distributed Systems, Machine Learning |📍Berlin 🇩🇪 | 📚 https://venkat.eu | 💬 https://twitter.com/Venkat2811