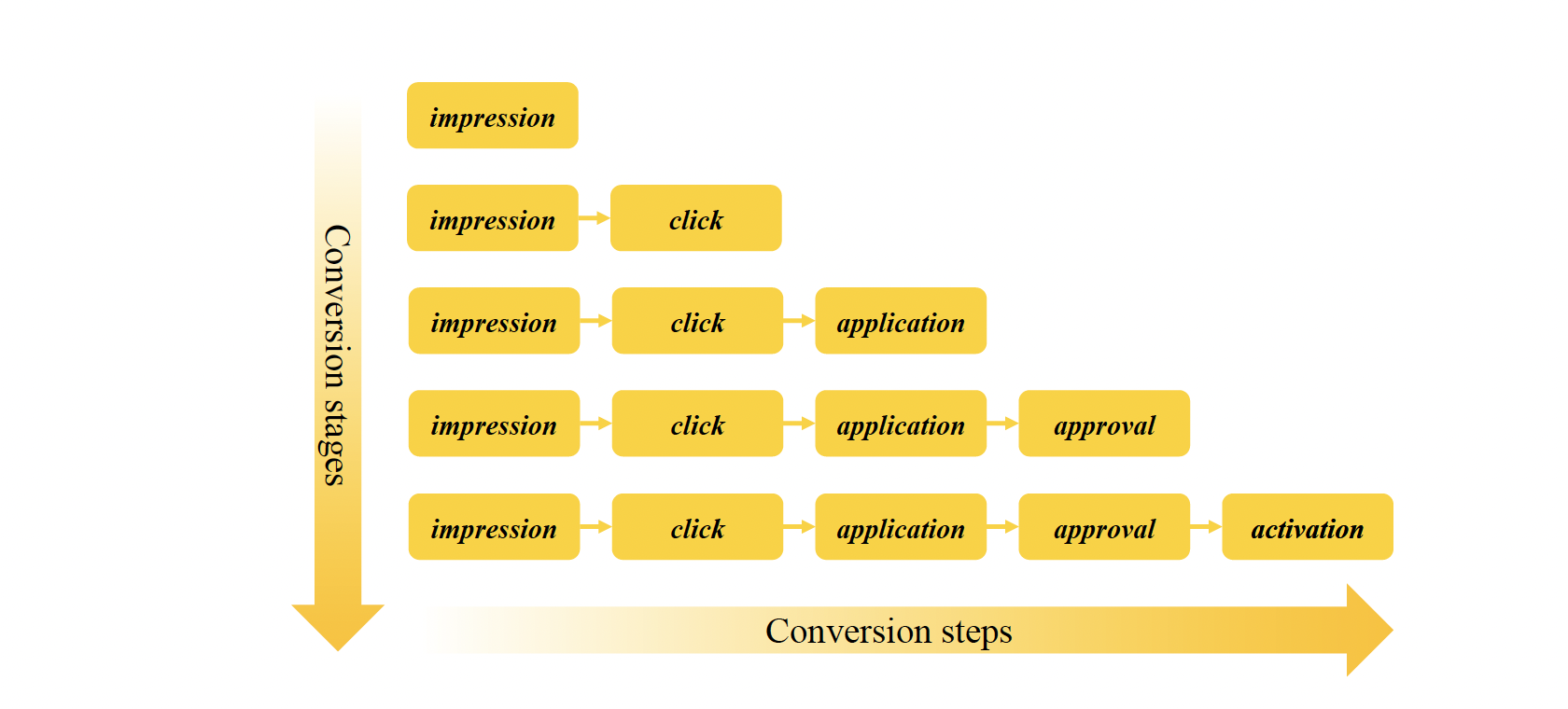
In this post I summarise the ideas in the paper "Modeling the Sequential Dependence among Audience Multi-step Conversions with Multi-task Learning in Targeted Display Advertising". You can find the full paper here.

Recap

In the previous post, we discussed how post-click behaviors can be used to add more supervision to ESMM modeling technique, further alleviating the data sparsity (DS) issue faced in post-click conversion rate (CVR) prediction. To achieve this,

1. user sequential behavior graph is created

2. actions post-click and pre-purchase are divided into Deterministic Actions (DAction) which are strongly correlated with purchase and Other Actions (OAction) to simplify the graph

3. finally, ESM2 model is trained for CTR (impression => click), CTAVR (impression => click => DAction) and CTCVR (impression => click => D(O)Action) => purchase) tasks which are defined over the entire space.

For more detailed summary, you can read ESMM et al. - Part 3.

---

Motivation Behind AITM

Customer acquisition in domains such as financial advertising (e.g. credit card advertising) have long multi-step conversion path (impression => click => application => approval => activation), as shown in the figure below, compared to e-commerce (impression => click => purchase).

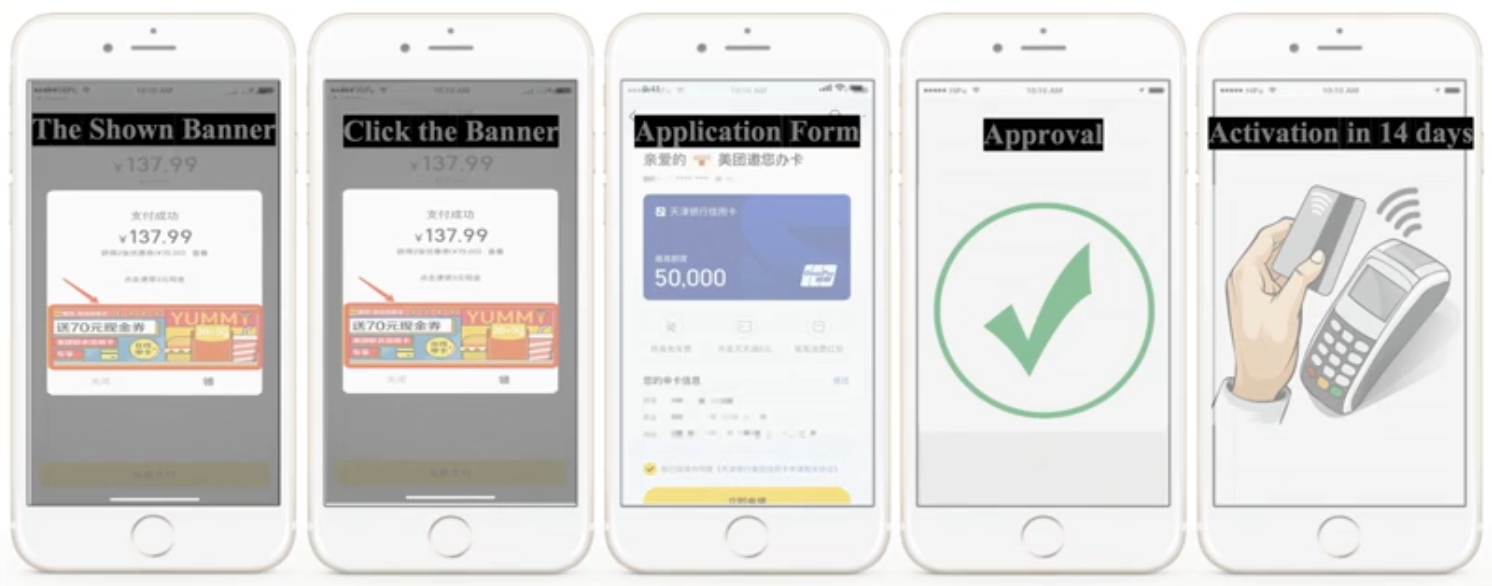
To model long-path sequential dependence is challenging for a number of reasons such as,

• Positive feedback at each subsequent step is sparser leading to increased class imbalance at later stages

• Rich transfer of information from the previous step which has more positive labels is critical to alleviate class imbalance of the subsequent steps

• For scenarios such as banner ads which take traffic away from other user conversion opportunities, if the sequentially dependent end-to-end conversion relation is not learned well, it could mean loss of business, i.e. we need to ensure

$$𝑦_1 \geq 𝑦_2 \geq \cdots \geq 𝑦_𝑇,\ (𝑦_𝑡 \in \{0, 1\},\ 𝑡 = 1, 2, \ldots ,𝑇)$$

Gap in Prior Methods

"In industry and academia, multi-task learning is a typical solution to improve the end-to-end conversion in the audience multi-step conversion task. Recently, considerable efforts have been done to model task relationships in multi-task learning."

In context of sequential task dependence modeling, I recommend you to read the literature review on multi-task learning (MTL) from the paper as well. Here I summarize it in brief.

Expert-Bottom Pattern

As shown in part (a) of the figure below, "The main idea of the Expert-Bottom pattern is to control how Expert modules are shared across all tasks at the bottom of the multi-task model, and the Tower modules at the top handle each task separately."

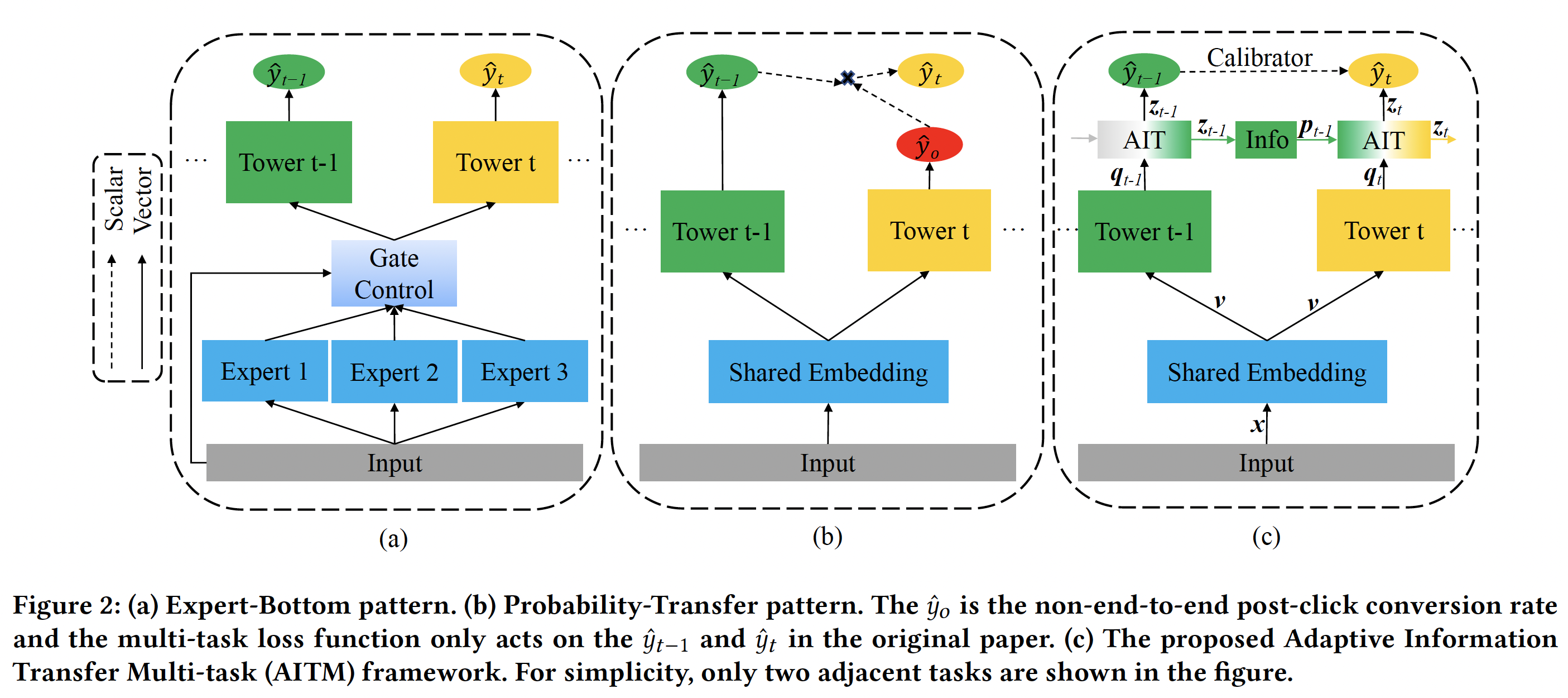
However, often richer representations are learned at the Tower modules at the top but these representations are not shared between the tasks to improve each other. This is a drawback of the expert-bottom pattern architectures.

Probability-Transfer Pattern

As shown in part (b) of the figure above, the current architectures enable sequential dependence learning via simple scalar probability multiplication. Learned representations which contain richer information are not transferred to the tasks. This limits the amount of information shared between the tasks.

Also, prior methods focus on non-end-to-end post-click conversion (e.g. p(purchase | click)) which do not fully address the challenges with end-to-end long multi-step conversions.

MTL Ranking System in Meituan App

"Meituan is a Chinese shopping platform for locally found consumer products and retail services including entertainment, dining, delivery, travel and other services." - Wikipedia

The MTL ranking system models four tasks click, application, approval and activation. Among them, the approval and activation are the main tasks, and the click and application are the auxiliary tasks.

Trade-off Between Businesses

Since a number of businesses are on-boarded on Meituan, to which business traffic should be diverted to depends on

• weight: an aggregate importance derived from the value of the business, value of the audience, value of audience to the business, and

• y_hat: the predicted conversion probability

as a result the final score is defined as,

$$score = weight * \hat{y}$$

and them the traffic is diverted to the business with the highest score. In practice this could mean e.g. whether the banner should show ad for a co-branded credit card or an offer for movie tickets.

Trade-off Between Objectives

The other interesting bit in the ranking system is shown in the figure below,

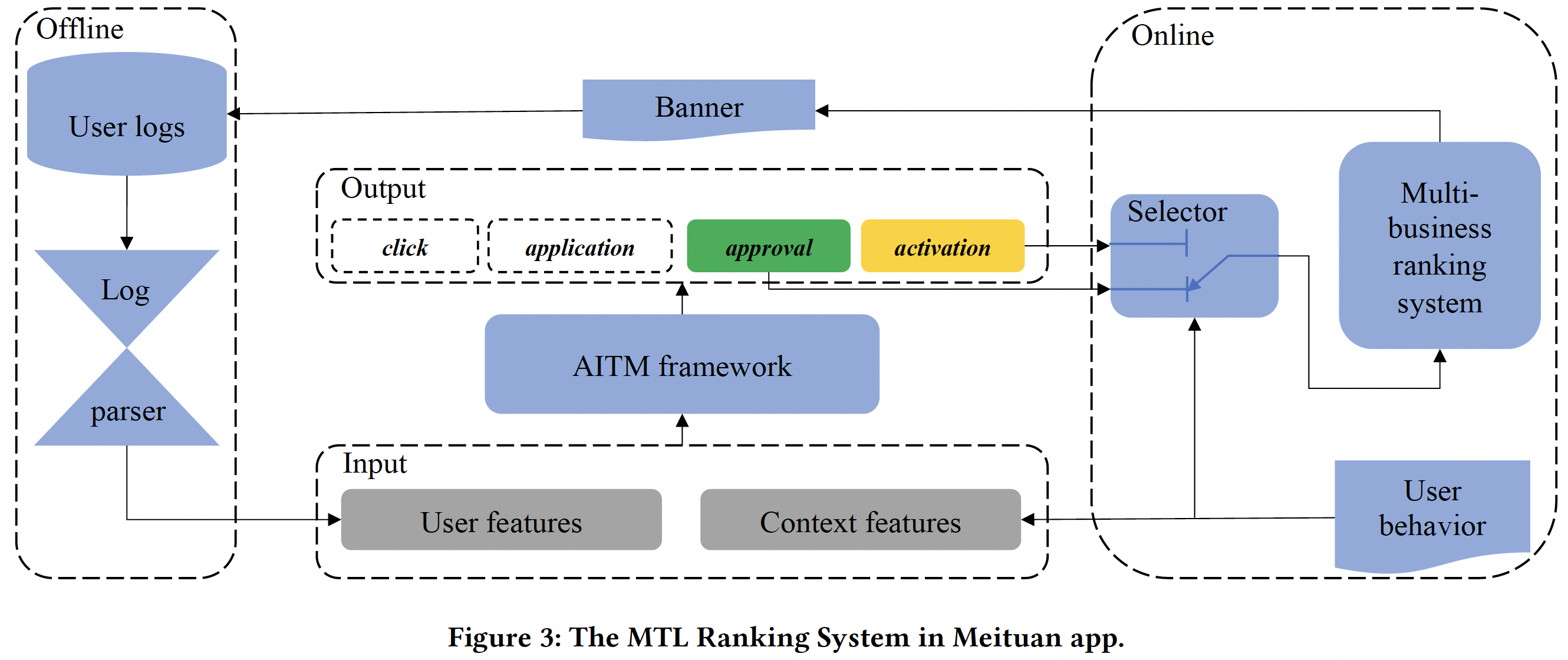
Notice the component Selector. Different businesses/clients have different objectives and selector helps in choosing the right trade-off between the corresponding ranking objectives. E.g. "Start-up banks often want to issue more credit cards to quickly occupy the market, while mature banks want to increase the activation rate to achieve rapid profits", therefore start-ups may want to focus only on approval rate prediction while mature banks may want to focus only on activation rate prediction.

Approach

Problem Formulation

The goal is to predict end-to-end conversion probability at each conversion step t given the input features x , i.e.

$$\hat{y}_t = p(y_1=1, y_2=1, \ldots, y_t=1|x)$$

Adaptive Information Transfer Multi-task (AITM) Framework

Data flow through the model is as follows,

$$\begin{gather*} \pmb{v} = [v_i;v_2;\ldots;v_{|\pmb{x}|}] \\ \\ \pmb{q_t} = f_t({\pmb{v}}) \\ \\ \pmb{z_1} = \pmb{q_1} \\ \\ \pmb{z}t = AIT(\pmb{p}{t-1}, \pmb{q}t) \\ \\ \pmb{p}{t-1} = g_{t-1}(\pmb{z}_{t-1}) \\ \\ \hat{y}_t = sigmoid(MLP(\pmb{z}_t)) \end{gather*}$$

where \(v_i\) is embedding of feature \(x_i \in x\).

New lets discuss the individual components.

Shared Embedding Module

The input x to AITM architecture is encoded to embedding v through a Shared Embedding Module. Here v is the concatenation of embedding of individual features in x.

$$\pmb{v} = [v_i;v_2;\ldots;v_{|\pmb{x}|}]$$

Shared Embedding Module helps address the data sparsity issue for the tasks with high class imbalance by sharing the embedding parameters with tasks with richer labels.

Task Tower Module

Input embedding v is fed to task specific modules. Details of task towers are not discussed in the paper but its hinted that they can be anything from simple MLPs to advanced models like NFM, DeepFM etc.

$$\pmb{q_t} = f_t({\pmb{v}})$$

where f(.) represents the task tower function.

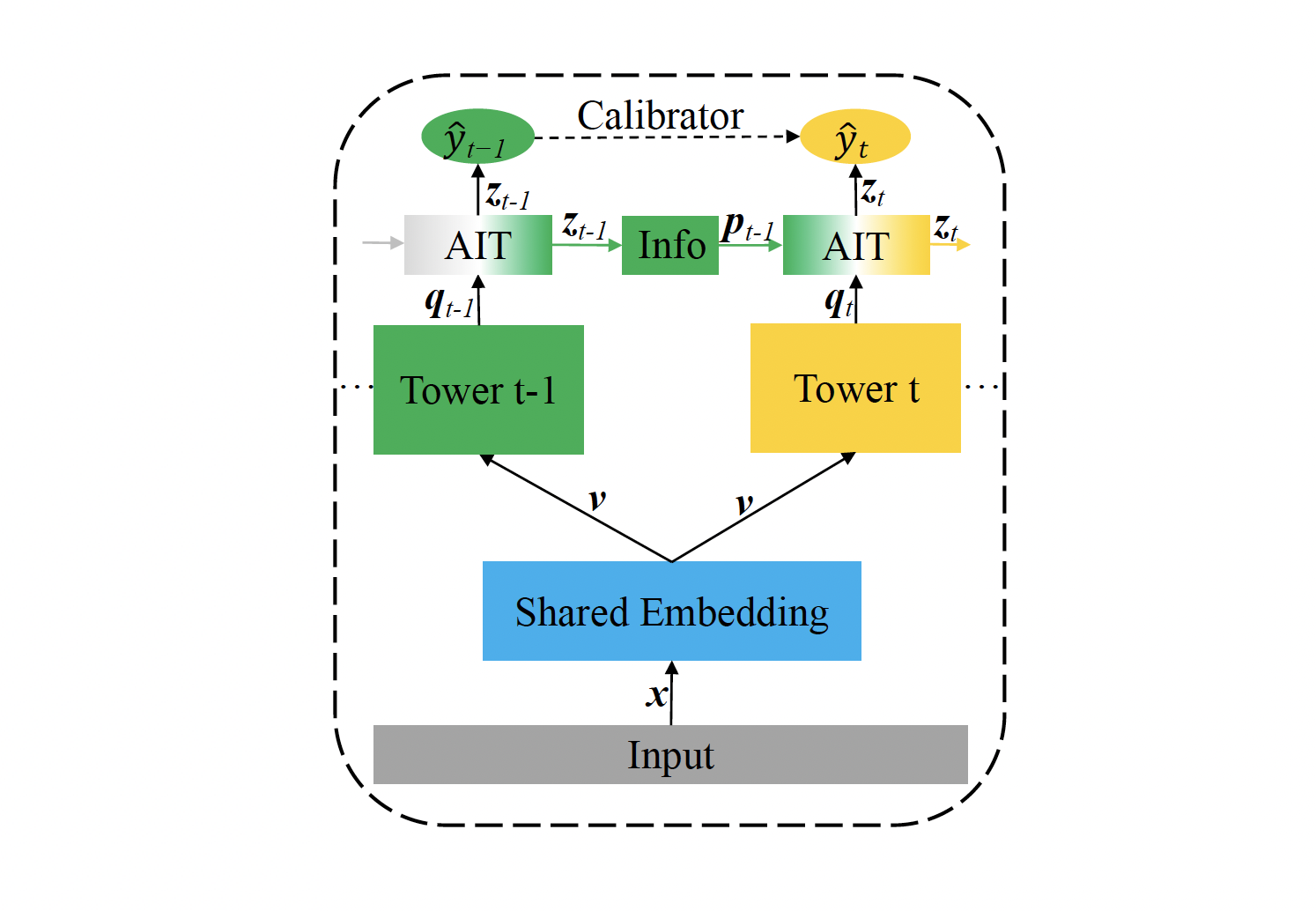
AIT Module

Output embedding of task tower q and transformed embedding from previous task tower p are given as input to the AIT module. This module then applies self attention over the two input embeddings and the resulting embedding is used to estimate the task probability.

$$\begin{gather*} \pmb{z_1} = \pmb{q_1} \\ \\ \pmb{p}{t-1} = g{t-1}(\pmb{z}_{t-1}) \\ \\ \pmb{z}t = AIT(\pmb{p}{t-1}, \pmb{q}_t) \\ \\ \end{gather*}$$

Notice that the rich representation learned at the previous task tower (t-1) is passed as information to the subsequent task (t) instead of just a scalar probability value.

Task Probability Prediction

Finally task probability is estimated as

$$\begin{gather*} \hat{y}_t = sigmoid(MLP(\pmb{z}_t)) \end{gather*}$$

Loss

Cross-entropy loss is used for individual conversion step prediction and a behavior loss calibrator is defined to enforce the sequential conversion dependence

$$𝑦_1 \geq 𝑦_2 \geq \cdots \geq 𝑦_𝑇$$

i.e. each subsequent end-to-end conversion step probability is lower than the last step probability.

Task Loss

$$\mathcal{L}_{ce}(\theta) = -\frac{1}{N} \sum{t=1}^{T}\sum_{(\pmb{x},y_t) \in D}^{N} ((y_tlog(\hat{y}_t) + (1-y_t)log(1-\hat{y}_t))$$

Behavioral Expectation Calibrator

$$\mathcal{L}_{lc}(\theta) = -\frac{1}{N} \sum{t=2}^{T}\sum_{\pmb{x} \in D}^{N} max(\hat{y}t - \hat{y}{t-1}, 0)$$

Final Loss

$$\mathcal{L}(\theta)= \mathcal{L}_{ce}(\theta)+ \alpha\mathcal{L}_{lc}(\theta)$$

Evaluation Metric

AUC is used to measure model performance for offline results and increase in conversion rate is used as a metric for online performance.

Result Discussion

Baselines

LightGBM, MLP, ESMM, OMoE (single gate MoE), MMoE, and PLE (Progressive Layered Extraction) models are used as baselines.

Offline Results

Improvement over LightGBM are reported in gains column in the result below.

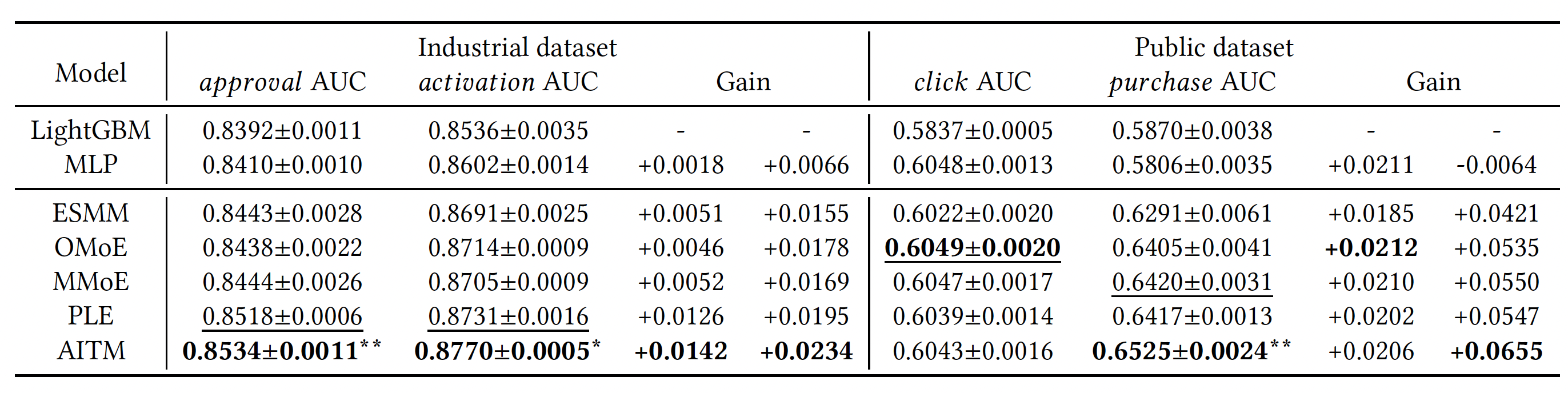
Industrial dataset means the Meituan dataset. The public dataset used is the Ali-CCP (Alibaba Click and Conversion Prediction) dataset.

Online Results

Gain in activation and conversion rates in the online experiment are shown below.

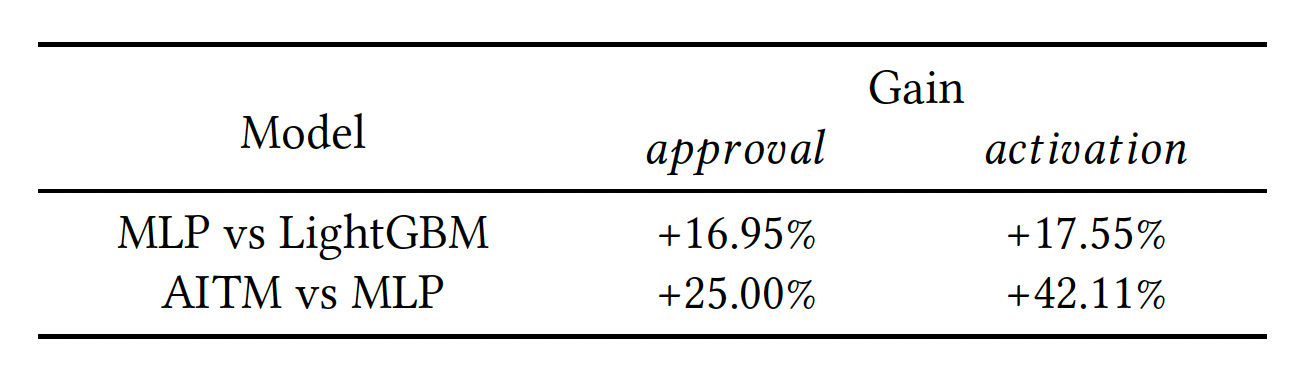
Notice that in offline, the AUC improvement of AITM over LightGBM was only 1.69% (0.0142 over 0.8392) for approval task and 2.74% (0.0234 over 0.8536) for activation task but the improvement in online experiment are huge!

Questions/Observations

1. How is the ranking done in online is not clearly stated, whether approval or activation task probability was used or a weighed sum of both?

2. Activation negatives were down sampled to 1% overall proportion during model training.

3. The TP999, TP9999 of the real-time prediction is less than 20ms, 30ms, which is impressive!

The paper also have very insightful analysis on how are the embeddings separated at the top of the tower and what kind of information transfer is observed. I recommend you to read it directly from the paper.