Graphing Linear Functions: A Comprehensive Guide

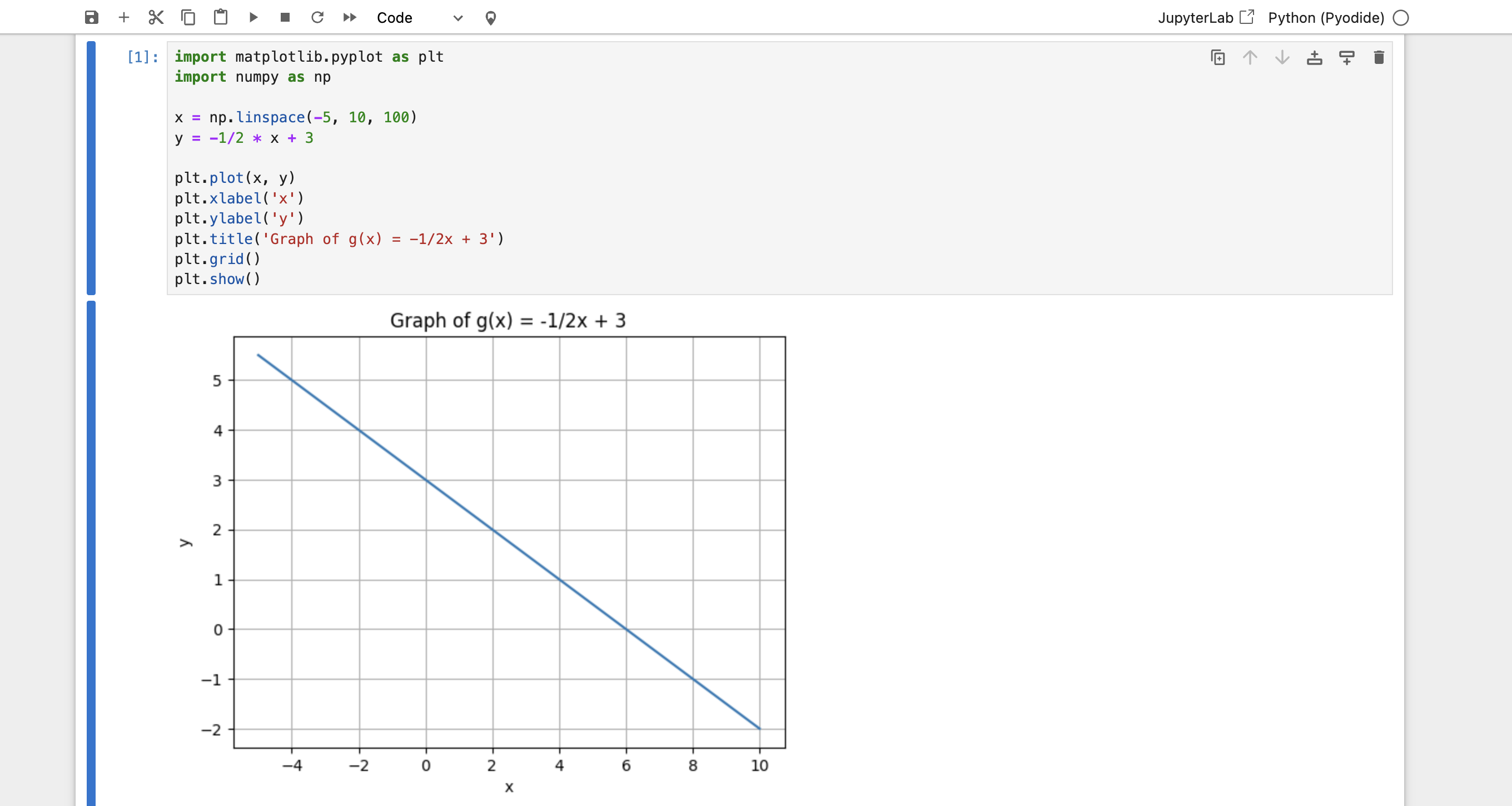
Introduction

Linear functions are a fundamental concept in mathematics, and graphing them is an essential skill for any student or professional. In this article, we will explore the graph of the linear function g(x) = -1/2x + 3, describing its key characteristics, slope, y-intercept, and what these characteristics indicate about the graph. We will also discuss the importance of graphing linear functions and provide a step-by-step guide on how to graph them.

Graphing Linear Functions

Graphing linear functions is a crucial skill in mathematics, as it allows us to visualize the relationship between variables. A linear function is a function in which the highest power of the variable(s) is 1. The graph of a linear function is a straight line, and it can be graphed using various methods, including plotting points, using the y-intercept and slope, and using transformations of the identity function.

The Graph of g(x) = -1/2x + 3

The graph of g(x) = -1/2x + 3 is a straight line that opens downward, indicating a negative slope. The line crosses the y-axis at the point (0, 3), which is the y-intercept. The graph also crosses the x-axis at the point (6, 0), which can be found by setting y = 0 and solving for x.

Slope: -1/2

The slope of the graph, -1/2, indicates that for every 1 unit increase in x, the value of y decreases by 1/2 unit. This negative slope means that the graph slopes downward from left to right, indicating an inverse relationship between x and y. The slope also tells us that the graph is relatively flat, with a gentle decline.

Y-Intercept: 3

The y-intercept of 3 indicates that the graph crosses the y-axis at the point (0, 3). This means that when x is 0, y is 3. The y-intercept is an important feature of the graph, as it provides a reference point for understanding the relationship between x and y.

Key Characteristics

• The graph is a straight line, indicating a linear relationship between x and y.

• The graph opens downward, indicating a negative slope.

• The graph crosses the y-axis at the point (0, 3), which is the y-intercept.

• The graph crosses the x-axis at the point (6, 0), which can be found by setting y = 0 and solving for x.

Visualizing the Graph with Python

To visualize the graph of g(x) = -1/2x + 3, we can use Python and the Matplotlib library. Here's an example code snippet:

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 10, 100)
y = -1/2 * x + 3

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Graph of g(x) = -1/2x + 3')
plt.grid()
plt.show()

This code generates a graph of the function g(x) = -1/2x + 3, which can be used to visualize the relationship between x and y.

Real-World Applications

The graph of g(x) = -1/2x + 3 has numerous real-world applications. For example, it could represent the cost of producing a certain product, where x is the number of units produced and y is the total cost. The negative slope would indicate that the cost decreases as the number of units produced increases. The y-intercept would represent the fixed cost of production, which is $3 in this case.

Graphing Linear Functions Using the Y-Intercept and Slope

Another way to graph linear functions is by using specific characteristics of the function rather than plotting points. The first characteristic is its y-intercept, which is the point at which the input value is zero. To find the y-intercept, we can set x = 0 in the equation.

The other characteristic of the linear function is its slope, which is a measure of its steepness. Recall that the slope is the rate of change of the function. The slope of a function is equal to the ratio of the change in outputs to the change in inputs. Another way to think about the slope is by dividing the vertical difference, or rise, by the horizontal difference, or run.

Let’s consider the following function:

f(x) = 1/2x + 1

The slope is 1/2. Because the slope is positive, we know the graph will slant upward from left to right. The y-intercept is1, so the graph will cross the y-axis at the point (0, 1).

To graph the function, we can start at the y-intercept and move up 1 unit and to the right 2 units. We can repeat this process until we have enough points to graph the line.

Graphing Linear Functions Using Transformations of the Identity Function

Another way to graph linear functions is by using transformations of the identity function. The identity function is the simplest linear function, with a slope of 1 and a y-intercept of 0.

To graph a linear function using transformations of the identity function, we can start by graphing the identity function and then applying the transformations.

Let’s consider the following function:

f(x) = 2x + 3

The slope is 2, and the y-intercept is 3. To graph the function, we can start by graphing the identity function, which has a slope of 1 and a y-intercept of 0.

Next, we can apply a vertical stretch by a factor of 2. This means that we will double the distance between each point on the graph.

Finally, we can shift the graph up by 3 units to account for the y-intercept.

Conclusion

In conclusion, graphing linear functions is an essential skill in mathematics, as it allows us to visualize the relationship between variables. The graph of g(x) = -1/2x + 3 is a straight line that opens downward, indicating a negative slope. The line crosses the y-axis at the point (0, 3), which is the y-intercept. The graph also crosses the x-axis at the point (6, 0), which can be found by setting y = 0 and solving for x. The slope of the graph is -1/2, indicating that for every 1 unit increase in x, the value of y decreases by 1/2 unit. The y-intercept is 3, indicating that when x is 0, y is 3. By understanding these key characteristics, we can gain valuable insights into the behaviour of the function. Whether in mathematics, science, or real-world applications, graphing linear functions is an essential tool for making informed decisions and predictions.

Thank you for reading this article about graphing the linear function g(x) = -1/2x + 3 and describing its key characteristics. We hope that this article has helped deepen your understanding of linear functions and their graphs.