May I have your attention please
 Nilay Gaitonde
Nilay Gaitonde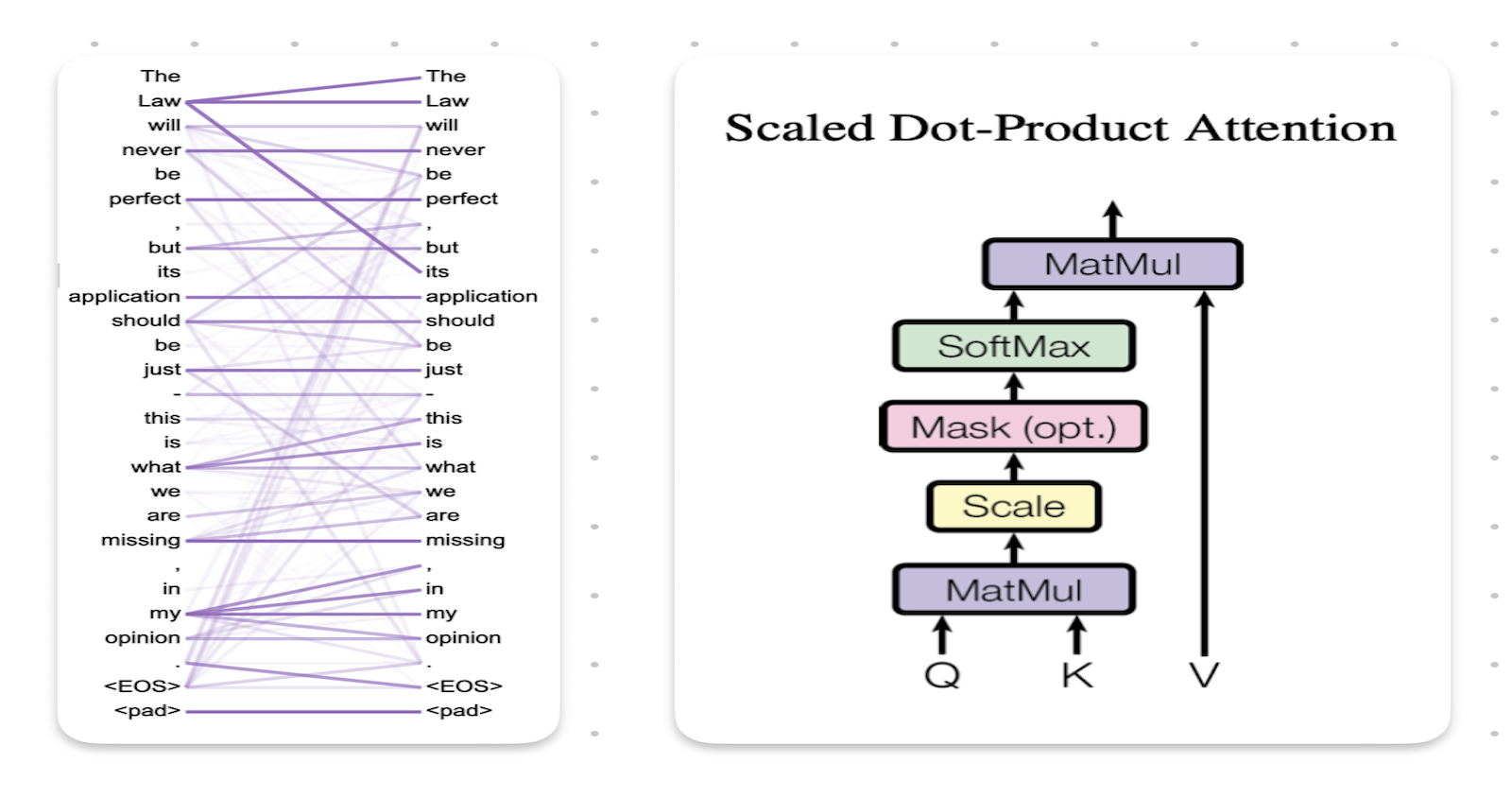
In 2017, researchers at Google released a landmark paper introducing a mechanism called "Transformer". The central idea behind Transformers was the Attention mechanism. The paper introduces a modification of the Bahdanau et al. attention mechanism called scaled dot product attention.
Motivation behind the attention mechanism
The attention mechanism was introduced in a 2014 paper called "Neural Machine Translation by Jointly Learning to Align and Translate" (Bahdanau et al.). The key idea of this paper was to use the attention mechanism to allow the encoder-decoder architecture to have variable length inputs instead of having encoding vectors with fixed length. Here the model learns to attend to different parts of the source sentence at each step of the output sequence generation.
What is attention?
The primary purpose of Attention mechanisms is to help the model focus on the important parts in large strings of text. This is really useful for NLP tasks where the input sequences can be long and we need to capture dependencies between values that are far away from each other in the sentence.
For example: "The student who got the highest grade in the class was awarded a scholarship by the principal". In this sentence there is a long range dependency between "the student" and "was awarded a scholarship". To correctly understand who was awarded the scholarship, the model needs to go back a few words in the sentence to the mention of "the student".
The main idea behind the aforementioned transformer paper, the attention mechanism proposed by Vaswani et al. is that the encoding representations can ask "queries" & get "answers" for these queries. In practice an attention layer is usually preceded by embedding layers.
Brief recap of embedding layers
The Embedding layer essentially learns a unique, dense "weight" vector representation for each token. A unique feature of this representation is that we can easily analyse the similarity of two tokens based on their embeddings.
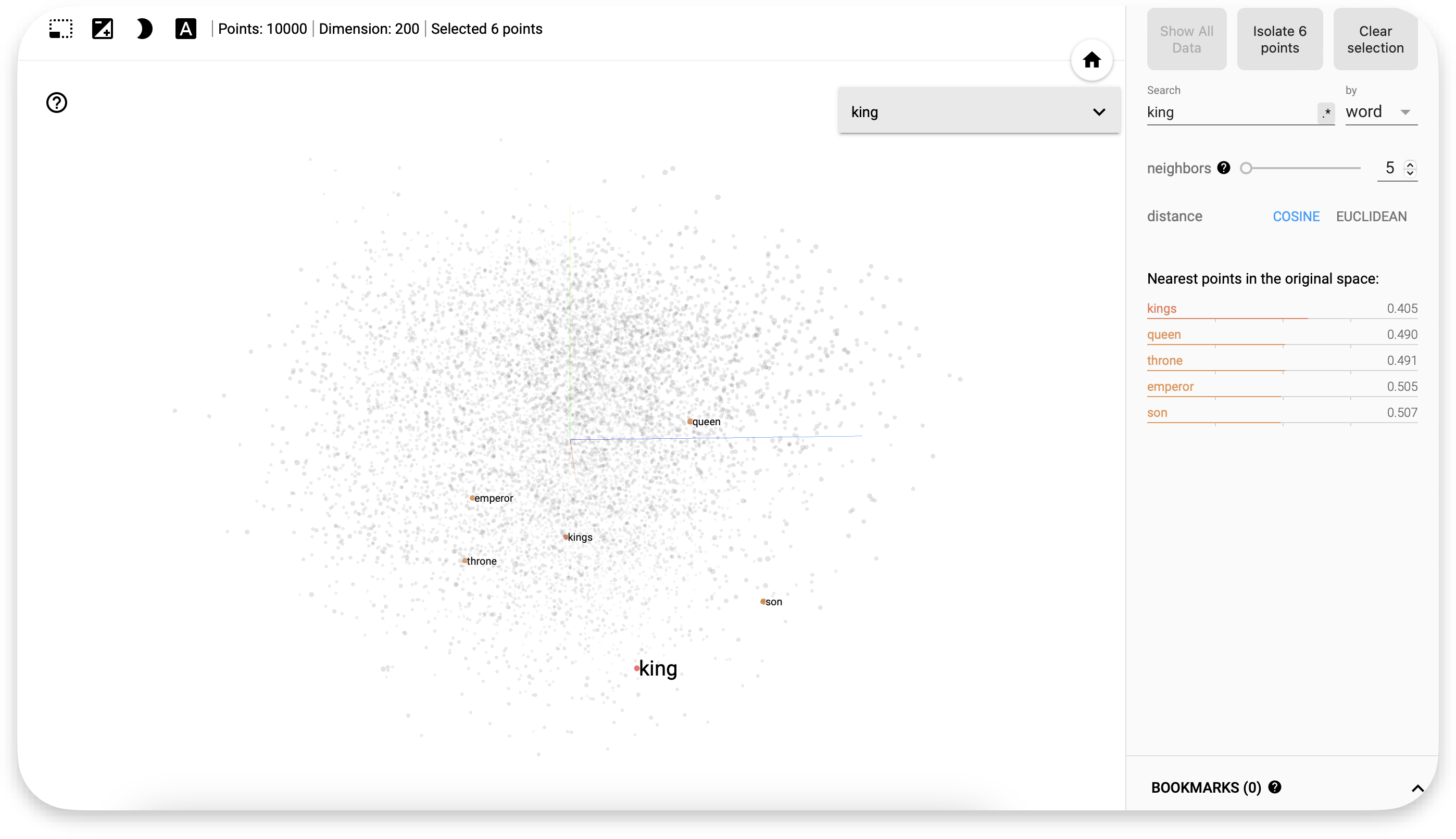
We can see that for the embedding of king the closest words (kings, queen, throne, emporer and son) are all closely related to king. You can try the same for any word at https://projector.tensorflow.org. A properly trained embedding layer must also be able to understand more complex relations.
For eg: The popular American show "The Simpsons" follows the Simpsons, a family consisting of Homer Simpson, Marge Simpson, Bart Simpson and Lisa Simpson. Bart and Lisa Simpson are siblings. A well trained embedding should be able to understand this correlation and should be able to tell us the answer for the following relation woman : ? :: man : bart

Before putting the embedding vectors into the Attention block we also encode their positions into the embeddings.
If you remember we said that the attention mechanism works by asking "queries" to the embedding vectors and expecting answers, so how would we make a set of encoded representations "talk" to each other? Everything in Deep Learning is based on weights and matrices, hence our goal with this attention mechanism is to use various weight vectors to calculate the probabilities.
Let's recall our example:
The student who got the highest grade in the class was awarded a scholarship by the principal
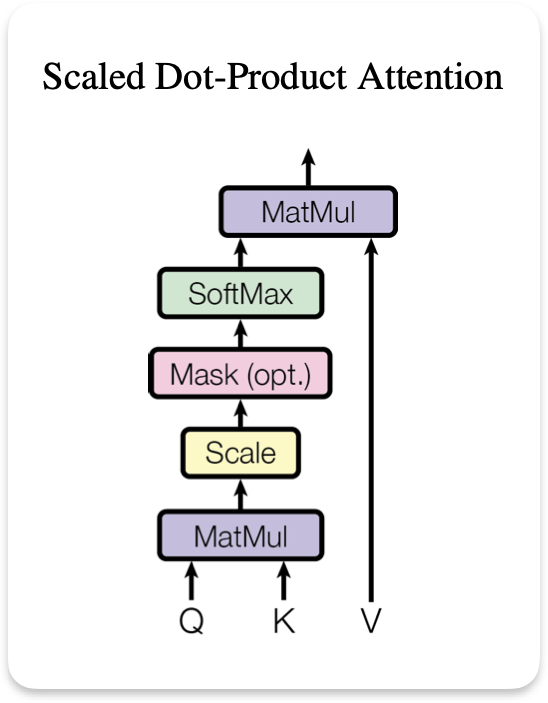
Let’s try to understand the attention architecture one block at a time, once you’ve understood the building blocks the full code is mentioned below. In the attention architecture we make use of 3 matrices: a key, query and a value matrix. The key and query matrix are learnable parameters of dimensions dk and the value matrix is of dimension dv. Thus the key and query matrices will be matrices of shape (embedding_dim, dk). Let us, for this example, assume embedding_dim = 10 and dk\=dv\=4, this means that the matrices will be of shape (10,4). What we want from these matrices is to give us weights that explain how closely related two tokens are.
For each word (assuming one token is one word) in a sequence let the word ask a “query” to the other words for example let each noun ask the rest of the words if an adjective is placed before it. The only noun that will answer that has an adjective placed before it is grade (with the adjective being highest), thus the attention score for this query must be very high. We can calculate these attention scores for each part of the input sequence by multiplying our key and value matrix. Let us try to understand this concept in code:
import torch
from torch import nn
import torch.nn.functional as F
# 1. Initialise key and query matrix
keys = nn.Linear(10,4)
queries = nn.Linear(10,4)
# 2. Generate key and query matrix for input sequence. Let x be an input sequence of size
# (5,10)
keys_value = keys(x)
#input is of shape (5,10) * keys of shape (10,4) -> keys_value matrix of shape (5,4)
queries_value = queries(x)
#input is of shape (5,10) * queries of shape (10,4) -> queries_value matrix of shape (5,4)
attention_scores = queries_value @ keys_value.T/(K.shape[-1]**0.5)
#queries_value of shape (5,4) * keys_value of shape (4,5) -> attention score matrix (5,5)
The attention score is a (5,5) matrix which shows some arbitrary numbers that don’t mean anything yet while we want to show is how well each token answers another token’s query i.e. for [i,j]th score, the ith token answers the jth token’s query with that much certainty. So with this logic the token for [“highest”, “grade”] will be high. We transform the matrix by applying the Softmax activation function. Applying Softmax on the attention_score will give us a matrix which will give us the proper probabilities.

You can see the change in the weights before and after applying Softmax.
attention_weights = F.softmax(attention_scores)
In the "Attention Is All You Need" paper Viswas et al. use scaled dot product to find these attention scores:
attention_scores = queries_value @ keys_value.T / (K.shape[-1]**0.5)
attention_weights = F.softmax(attention_scores)
Whykeys_value.T?
The shape of queries_values, keys_value is (5,4) and (5,4) respectively. Trying to matrix multiply this will give an error since for two matrices A[p,q] and B[r,s] to be multiplied q must be equal to r. Hence we multiply queries_value with the transpose of keys_value.
We now have a set of weights that represent how closely related two tokens are, but now we need to actually apply these weights on the input data. To do this we use a values_vector that is initiated and implemented in a similar way to keys_value and queries_value
values = nn.Linear(10,4)
values_vector = values(x)
output = attention_weights @ values_vector
The value vectors act as the "information carriers" from the input sequence, and the attention weights modulate how much of each value vector should contribute to the final output representation.
Masking
Masking is used in attention mechanisms to ensure that the tokens don't learn from future data. A common way to do this is to make all the elements above the diagonal in the matrix -∞ so that after Softmax it becomes 0. While this masking logic is important for certain tasks like language modelling, it can be restrictive and limiting for more complex use cases like machine translation and open-ended generation, where attending to future context is often crucial for producing contextually relevant outputs. You can read more about masking here or see a video here
The entire attention block
class Attention(nn.Module):
def __init__(self,head_size, n_embed):
super().__init__()
self.keys = nn.Linear(n_embed,head_size)
self.queries = nn.Linear(n_embed,head_size)
self.values = nn.Linear(n_embed,head_size)
def __call__(self,X):
K = self.keys(X)
Q = self.queries(X)
V = self.values(X)
e = Q @ K.transpose(1,2) / (K.shape[-1]**0.5)
attention_scores = e.masked_fill((torch.tril(torch.ones(X.shape[1], X.shape[1]))==0),-torch.inf)
attention_weights = F.softmax(attention_scores)
out = attention_weights @ V
return out
Conclusion
In this blog i've tried to explain how a basic attention block works. In practice, transformers usually use Multi-Head Attention. Multi-Head Attention is essentially just like a concatenation of a number of attention blocks together.
Attention is an extremely important part of Transformer models as it allows for the model to dynamically weigh and combine information from different parts of the input sequence and effectively modelling long-range dependencies and capturing intricate details.
I hope through this article you've understood about the basic working of an attention mechanism, specifically the scaled dot product attention mechanism. I have also implemented the attention mechanism from scratch to perform sentiment analysis. The code for that can be found here and for any queries you can send me a mail
Subscribe to my newsletter
Read articles from Nilay Gaitonde directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
