Binary Tree Maximum Path Sum (Hard)

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

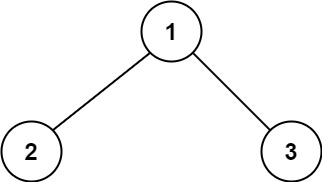
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

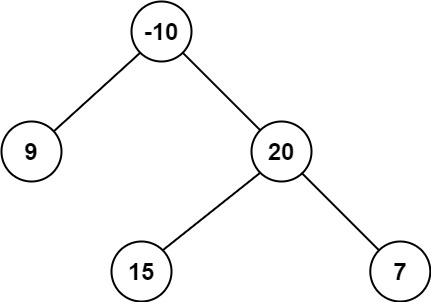
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

1) Explain the problem

We need to find the maximum path sum in a binary tree. A path can start and end at any nodes in the tree, and it must be a sequence of connected nodes. The goal is to find the path with the highest sum of node values.

2) Short easy to remember solution/approach

Use depth-first search (DFS) to traverse the tree. For each node, calculate the maximum path sum passing through the node, including the node itself. Keep track of the global maximum path sum encountered during the traversal.

3) Solution in Javascript with code commenting

class TreeNode {
    constructor(val, left = null, right = null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

function maxPathSum(root) {
    let maxSum = -Infinity;

    function dfs(node) {
        if (!node) return 0;

        // Calculate the maximum path sum for the left and right subtrees
        let leftMax = Math.max(dfs(node.left), 0); // If negative, use 0
        let rightMax = Math.max(dfs(node.right), 0); // If negative, use 0

        // Calculate the maximum path sum passing through the current node
        let currentMax = node.val + leftMax + rightMax;

        // Update the global maximum path sum
        maxSum = Math.max(maxSum, currentMax);

        // Return the maximum path sum including the current node
        return node.val + Math.max(leftMax, rightMax);
    }

    dfs(root);
    return maxSum;
}

// Example usage:
let root = new TreeNode(-10);
root.left = new TreeNode(9);
root.right = new TreeNode(20);
root.right.left = new TreeNode(15);
root.right.right = new TreeNode(7);

console.log(maxPathSum(root)); // Output: 42

4) Explanation of the solution in an easy-to-understand way. Explain it like a 10yo.

Imagine you are walking through a forest and collecting apples from trees. Each tree has a number of apples (which could be negative if some trees are bad). You want to find the path where you collect the most apples. You can start and end at any tree, and you can only move to neighboring trees. You try different paths, and whenever you find a better path with more apples, you remember it. Finally, you know the best path with the most apples.

5) Code explanation in pointers

• Define a TreeNode class to represent each node in the tree.

• Create a maxPathSum function that:

  • Initializes a variable maxSum to keep track of the global maximum path sum.

  • Defines a helper function dfs to perform DFS:

    • If the node is null, return 0.

    • Recursively calculate the maximum path sums for the left and right subtrees, using 0 if a subtree's path sum is negative.

    • Calculate the maximum path sum passing through the current node.

    • Update the global maximum path sum.

    • Return the maximum path sum including the current node.

  • Start the DFS traversal from the root.

  • Return the global maximum path sum.

6) Complexities

• Time Complexity: (O(n)) - Each node is visited once.

• Space Complexity: (O(h)) - Where (h) is the height of the tree. This is due to the recursion stack used for DFS.