Understanding In-place Reversal of a Linked List

The In-place Reversal of a Linked List is a common technique for solving linked list problems. It involves reversing the linked list without using extra space, typically by manipulating the pointers of the nodes directly.

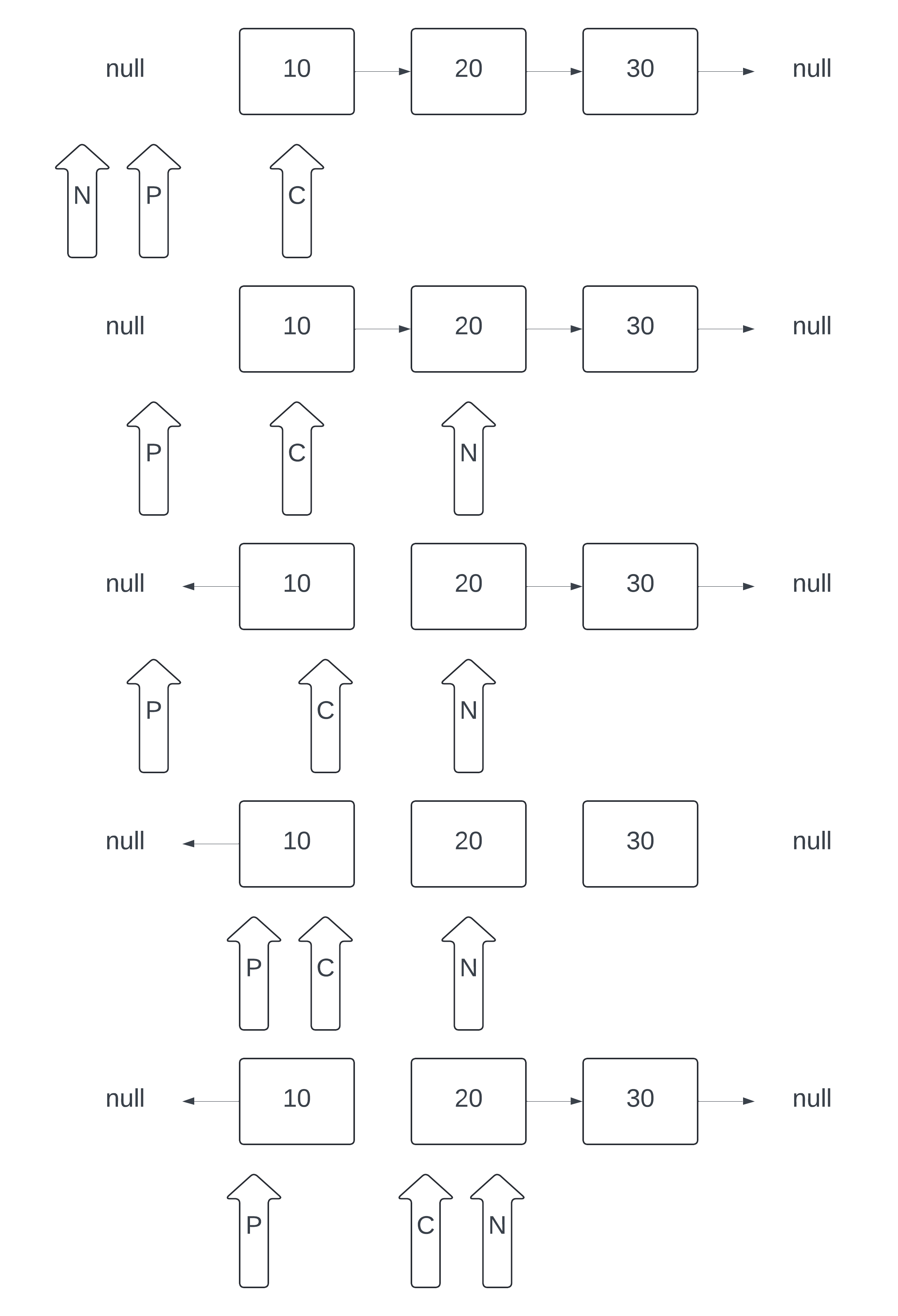
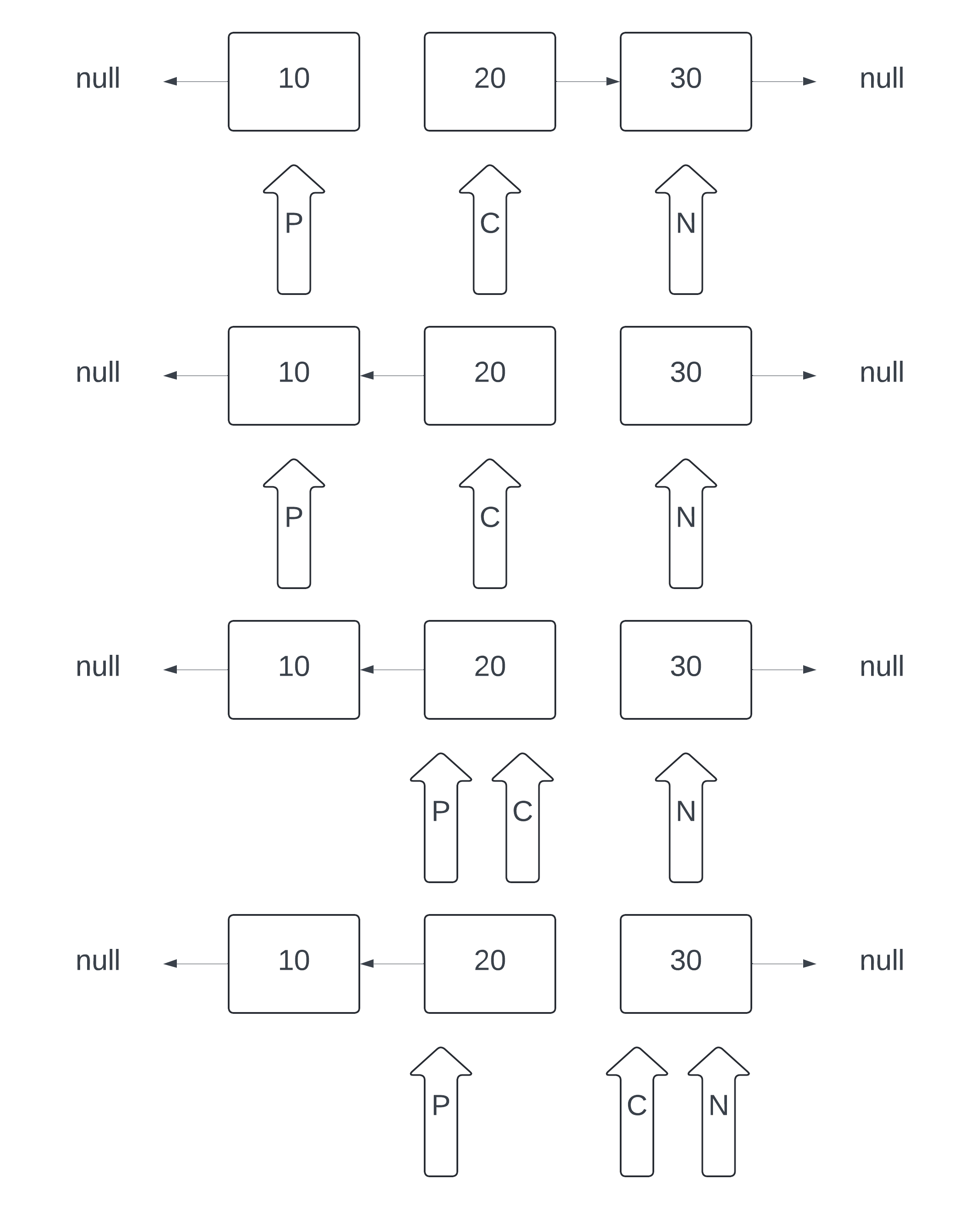
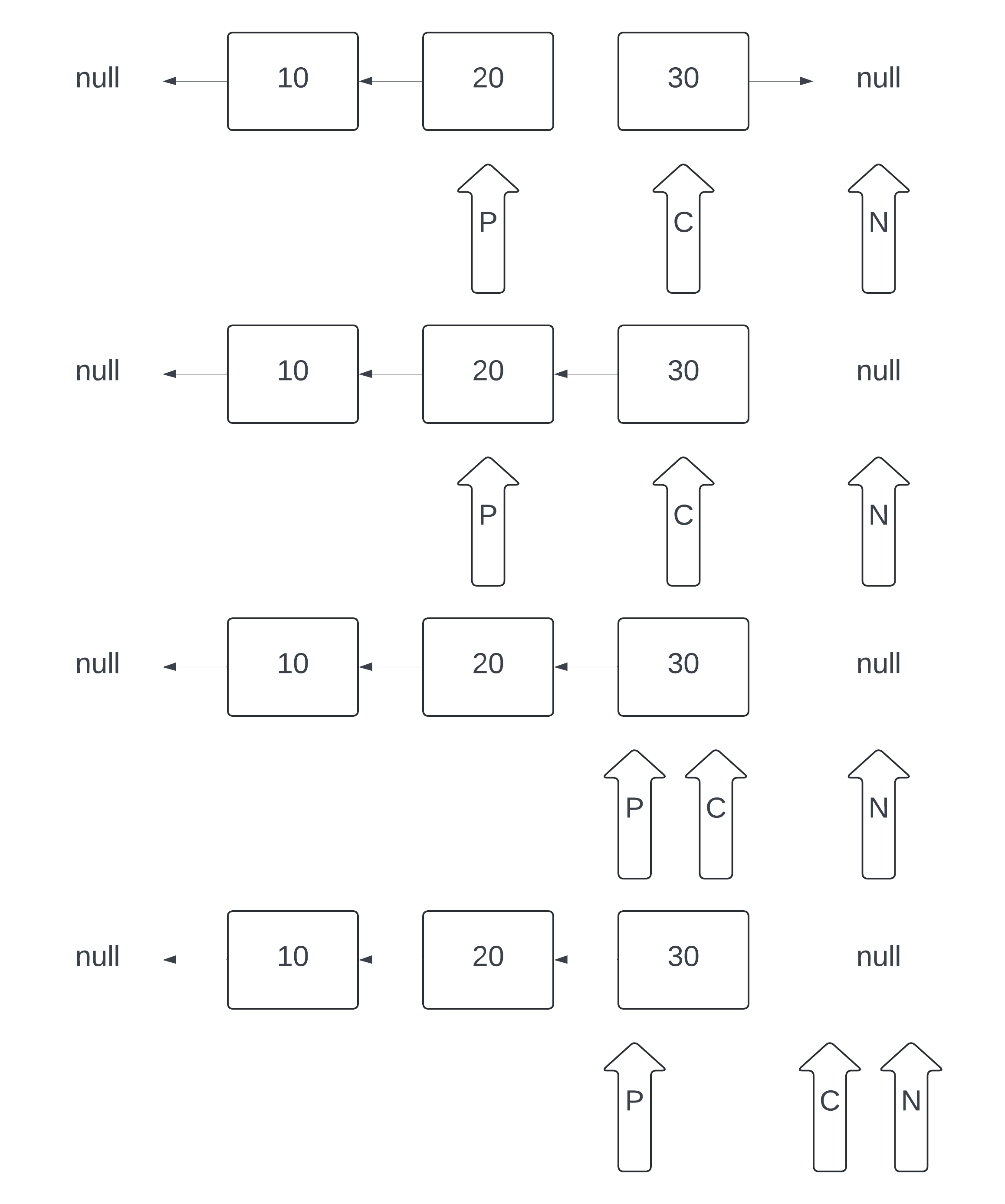
Process

1. Initialization: Start by initializing three pointers: prev, current, and next. Initially, prev is set to null, current is set to the head of the linked list, and next is set to null.

2. Traversal: Traverse the linked list using the current pointer. For each node, perform the following steps:

   • Store the next node in next (i.e., next = current.next).

   • Reverse the direction of the current node's pointer to point to prev (i.e., current.next = prev).

   • Move the prev pointer to the current node (i.e., prev = current).

   • Move the current pointer to the next node (i.e., current = next).

3. Termination: The process terminates when the current pointer reaches the end of the linked list (i.e., current becomes null). At this point, prev will be pointing to the new head of the reversed linked list.

When to Use

1. Reversing a Linked List: To reverse a linked list in-place is a common operation in many linked list problems.

2. Partial Reversal: To reverse a portion of a linked list, such as reversing a sublist or reversing every k nodes in a linked list.

How Does It Reduce Time Complexity?

1. Linear Time Complexity: The in-place reversal of a linked list has a time complexity of O(n), where n is the number of nodes in the linked list. This is because each node is visited exactly once.

2. Constant Space Complexity: The space complexity is O(1) since no additional space is used other than a few pointers.

Example problem for better understanding

Reverse Linked List

Thank you for reading!

You can support me by buying me a book.