Understanding the Topological Sort algorithm
 Vineeth Chivukula
Vineeth ChivukulaTopological Sort is a linear ordering of vertices in a directed acyclic graph (DAG) such that for every directed edge 𝑢→𝑣, vertex 𝑢 comes before 𝑣 in the ordering. This pattern is particularly useful in problems involving scheduling, dependency resolution, and various other applications where tasks or events have dependencies that must be respected.
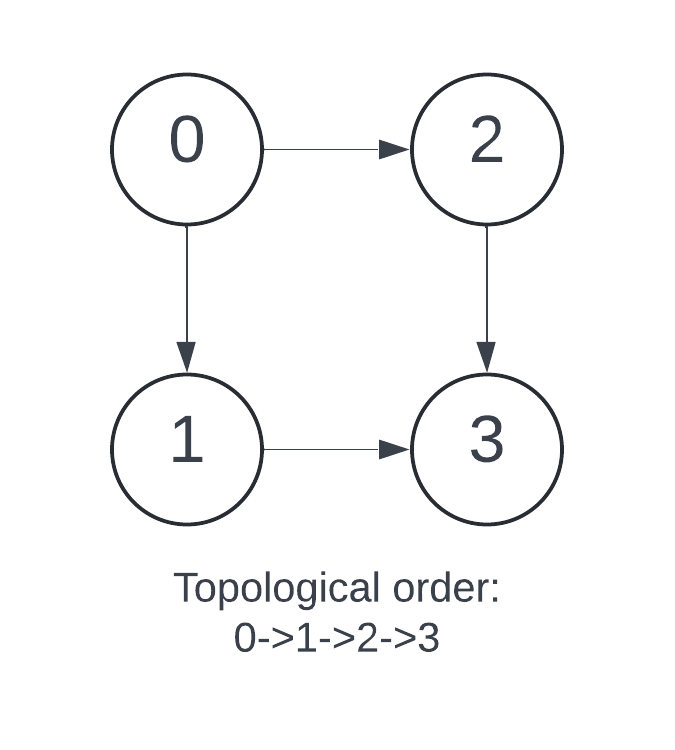
Process
Initialization: Create an array
inDegreeto count each vertex's incoming edges (in degrees). Create a list of listsgraphto represent the graph. Each index of the list corresponds to a vertex, and the value at that index is a list of its children.Build the Graph and Count in degrees: Add edges to the graph from the input. For each edge (A -> B):
Add B to the list of children for vertex A in the
graph.Increment the count in the
inDegreearray for vertex B (since it has an incoming edge from A).
Find Sources (Vertices with 0 In-degrees): Iterate through the
inDegreearray. Any vertex with an in-degree of 0 is a source. Store these sources in a Queue.Topological Sort: Start with the sources in the queue. For each source:
Remove it from the queue.
Add it to a sorted list
sortedOrder.Look at its children in the
graph.Decrease the in-degree of each child by 1.
If any child's in-degree becomes 0, add it to the sources queue.
Continue this process until the sources queue is empty.
Termination: The process terminates when the queue is empty. If the
sortedOrderlist contains all vertices, the sort is successful. If any vertices are left unprocessed, the graph contains a cycle, and a topological sort is impossible.
When to Use
Task Scheduling: To determine the order in which tasks should be performed when tasks have dependencies.
Dependency Resolution: To resolve dependencies between modules or packages in a software system.
Course Scheduling: To determine the order in which courses should be taken when courses have prerequisites.
Time Complexity
The topological sort algorithm has a time complexity of O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because each vertex and each edge is processed exactly once.
Implementation
import java.util.*;
public class TopologicalSort {
public static List<Integer> topologicalSort(int vertices, List<List<Integer>> edges) {
List<Integer> sortedOrder = new ArrayList<>();
if (vertices <= 0) {
return sortedOrder;
}
// 1. Initialize the graph
// count incoming edges
int[] inDegree = new int[vertices];
// adjacency list graph
List<List<Integer>> graph = new ArrayList<>();
for (int i = 0; i < vertices; i++) {
graph.add(new ArrayList<>());
}
// 2. Build the graph
for (List<Integer> edge : edges) {
int parent = edge.get(0);
int child = edge.get(1);
// put the child into its parent's list
graph.get(parent).add(child);
// increment child's inDegree
inDegree[child]++;
}
// 3. Find all sources/vertices with 0 inDegrees
Queue<Integer> sources = new LinkedList<>();
for (int i = 0; i < inDegree.length; i++) {
if (inDegree[i] == 0) {
sources.add(i);
}
}
// 4. For each source, add it to sortedOrder and decrement its children inDegree
// if a child becomes 0, add to source queue
while (!sources.isEmpty()) {
int vertex = sources.poll();
sortedOrder.add(vertex);
for (int child : graph.get(vertex)) {
// get the nodes children to decrement their inDegree
inDegree[child]--;
if (inDegree[child] == 0) {
sources.add(child);
}
}
}
// topological sort is not possible as the graph has a cycle
if (sortedOrder.size() != vertices) {
return new ArrayList<>();
}
return sortedOrder;
}
public static void main(String[] args) {
int vertices = 4;
List<List<Integer>> edges = new ArrayList<>();
edges.add(Arrays.asList(0, 1));
edges.add(Arrays.asList(0, 2));
edges.add(Arrays.asList(2, 3));
edges.add(Arrays.asList(1, 3));
List<Integer> sortedOrder = topologicalSort(vertices, edges);
if (sortedOrder.isEmpty()) {
System.out.println("Graph has a cycle, topological sorting is not possible.");
} else {
System.out.println("Topological Sort: " + sortedOrder);
}
}
}
Example problem for better understanding
Course Schedule
Thank you for reading!
You can support me by buying me a book.
Subscribe to my newsletter
Read articles from Vineeth Chivukula directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Vineeth Chivukula
Vineeth Chivukula
There's this guy who's mad about editing and programming. It's his jam, you know?