Introduction

While solving Engineering, Scientific, Mathematical Modeling Problems error can be arise due to several factors.

1. The error may be in the modeling technique

2. Errors may arise from mistakes in programs themselves or measurement of physical entities.

But in applications of numerical methods we encounter two type of errors -

1. Round-off Error

2. Truncation Error

Sources of Error - Round-off Error

What is a round off error?

In everyday life we're using mathematics and computer. Sometimes we have to use fractional numbers for example 1/3. A computer can only represent a number approximately. The example we take 1/3 can be represented in PC as 0.333333. Then the round-off error, in this case, is 1/3 − 0.333333 =0.00000033¯. Then there are other numbers that cannot be represented exactly.

What Problems can be created by round-off errors?

Round-off errors while storing numbers or while conducting arithmetic operations can propagate errors. Here is a real-life example of what happened when a small round-off error was responsible for a tragedy during the 1991 US-Iraq war.

Twenty-eight Americans were killed on February 25, 1991. An Iraqi Scud hit the Army barracks in Dhahran, Saudi Arabia. The Patriot defense system had failed to track and intercept the Scud. What was the cause of this failure?

The Patriot defense system consists of an electronic detection device called the Range Gate. It calculates the area in the air space where it should look for a Scud. To find out where it should aim next, it calculates the velocity of the Scud and the last time the radar detected the Scud. Time is saved in a register that has 2424 bits in length. Since the internal clock of the system is measured for every one-tenth of a second, 1/10 is expressed in a 2424 bit-register as 0.000110011001100110011000.00011001100110011001100. However, this is not an exact representation. In fact, it would need infinite numbers of bits to represent 1/10 exactly.

We can take a look to check how much it differs from the expected value:

To see that, we convert the binary number to decimal number-

The battery was on for 100 consecutive hours, hence causing an inaccuracy of

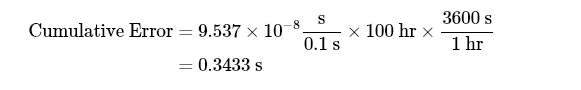
For the Patriot missile defense system, the target is considered out of range if the shift is more than than 137 m. The shift of larger than 137 m resulted in the Scud not being targeted and hence killing 28 Americans in the barracks of Saudi Arabia.

Effect of Carrying Significant Digits

The concept of significant digits (or significant figures) is crucial in scientific calculations to ensure accuracy and precision. Significant digits are the meaningful digits in a number, which contribute to its accuracy. When performing calculations, failing to carry enough significant digits can lead to significant errors in the final result. This effect can be illustrated with a real-life example involving financial transactions.

Real-Life Example: Financial Transactions

Imagine you are managing a large sum of money in an investment fund. Let’s say the total investment amount is $1,000,000, and you are tracking daily interest calculations.

1. Using Fixed Decimal Places:

   • Suppose the interest rate is 0.035% per day.

   • Calculating the daily interest: (1,000,000 \times 0.00035 = 350) dollars.

   • If you only use two decimal places for calculations, you might round intermediate results, say, to $350.00 for each day.

2. Cumulative Effect:

   • Over a year, the cumulative interest would be: (350 \times 365 = 127,750) dollars.

3. Using Sufficient Significant Digits:

   • Instead, if you carry more significant digits in your calculations, you would maintain higher precision.

   • For instance, if the actual daily interest calculated to more significant digits is $350.123456, you might not round off in intermediate steps.

   • Over a year, the cumulative interest calculated without prematurely rounding would be more accurate.

Demonstrating the Difference

Let’s illustrate with specific numbers:

1. Daily Interest Calculation:

   • Accurate daily interest: (1,000,000 \times 0.00035 = 350) dollars (simple case for illustration).

2. Accumulated Interest (With Rounding to Two Decimal Places):

   • Rounding daily: $350.00

   • Yearly cumulative (rounded daily): (350 \times 365 = 127,750) dollars.

3. Accumulated Interest (Without Rounding):

   • Precise daily interest: $350.123456

   • Yearly cumulative (precise daily): (350.123456 \times 365 \approx 127,544.062) dollars.

4. Difference:

   • The difference between rounded and unrounded cumulative interest is: (127,750 - 127,544.062 = 205.938) dollars.

Impact on Real Life

In the real world, especially in finance, engineering, and scientific research, small discrepancies can accumulate over time and lead to significant differences. For example:

• Finance: Small rounding errors in daily transactions can lead to large discrepancies in account balances over time.

• Engineering: Precision in measurements and calculations can affect the integrity and safety of structures.

• Science: Accurate significant digits ensure the reliability of experimental results and conclusions.

By understanding the importance of carrying sufficient significant digits in calculations, professionals can minimize errors and ensure accurate, reliable results in their work.

Truncation Error

Introduction

Truncation error is defined as the error caused by mathematical procedures. It refers to the difference between the actual value of the function and truncated value of the given function. The truncated value of the functions is the approximated value up to a given number of digits. For example, the speed of light in vacuum is 2.99792458 × 10⁸ ms^-1. The truncated value up to two decimal places is 2.99 × 10⁸. Hence the truncation error is the difference between 2.99792458 × 10⁸ and 2.99 × 10⁸, which is 0.00792458 × 10^8, or in scientific notation, it is 7.92458 × 10⁵.

For example, the Maclaurin series for e^xis given as

The series has an infinite number of terms but when we are using this series to calculate only a finite number of terms can be used. The truncation error -

Let's take another example-

Using the concept of the relative approximate error to illustrate through an example how truncation error can be controlled.

Solution:

Let us see how many terms need to be considered to calculate e1.2 within 1% pre-specified tolerance.

In the below table we tabulate the value of e^1.2, approximate error and absolute relative approximate error as a function of the number of terms of the series used, n.

The reported value of e1.2 is 3.3151 and is shown up to 5 significant digits. As a side note, the exact value, up to 5 significant digits, of e1.2 is 3.3201.

We can take Differentiation function and Integral function as an example to learn truncation error.

Differential Equation:

Since we are calculating f'(3) so x=3

after taking value of x we get

f'(x)=6

Next, while we take value of h

Given the step size of ℎ=0.2, we get

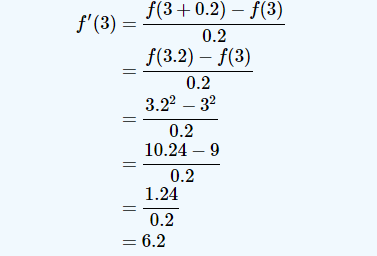
and the truncation error-

Truncation Error = Exact Value−Approximate

Value=6−6.2=−0.2

When solving differential equations numerically, we often use methods such as Euler's method or the Runge-Kutta method. These methods approximate the solution by taking finite steps.

• Example: Consider the differential equation (dy/dx = f(x, y)).

  • In Euler's method, the next value (y_{n+1}) is estimated using: (y_{n+1} = y_n + h f(x_n, y_n)), where (h) is the step size.

  • The truncation error in this method is proportional to the step size (h). Specifically, the error per step is (O(h^2)), and over (N) steps, the global truncation error is (O(h)).

Integral Equations

When evaluating integrals numerically, methods such as the trapezoidal rule or Simpson's rule are employed. These methods approximate the area under a curve by summing the areas of geometric shapes.

• Example: Consider the integral (\int_a^b f(x) , dx).

  • Using the trapezoidal rule, the integral is approximated as: (\int_a^b f(x) , dx \approx \frac{h}{2} \left[f(a) + 2 \sum_{i=1}^{N-1} f(x_i) + f(b)\right]), where (h) is the width of each subinterval.

  • The truncation error for the trapezoidal rule is (O(h^2)). Reducing the step size (h) decreases the error, but cannot eliminate it completely.

Importance of Understanding These Errors

Recognizing and understanding these sources of error is essential for improving the accuracy of numerical computations. By refining methods and choosing appropriate step sizes, we can minimize these errors and achieve more precise results.

In this article, I aim to shed light on how these errors manifest in numerical methods and provide insights into mitigating their effects. Whether you’re solving differential equations or evaluating integrals, being aware of round-off and truncation errors will enhance your computational techniques and results.

Now you are able to -

1. Recognize that there are two inherent sources of error in numericalmethods round-off and truncation error

2. define and exemplify round-off errors