Machine Learning: Relation between SVM and Lagrange

Engineering Students especially at Mumbai University won't forget the M4 and Lagrange's Multiplier which few of the students skipped, including me but if you are passionate about machine learning skipping mathematics behind it won't work.

We studied How Lagrange's multiplier helps optimize functions subject to constraints. Similarly, it's a way more crucial aspect of Machine learning techniques.

That technique is SVM (Support Vector Machine) first let's see what SVM is and how Lagrange helps in SVM and eventually in ML.

WHAT IS SVM?

An SVM is a type of classifier that finds the best line (or hyperplane) to separate different classes in the data. The goal is to make the distance between this line and the closest data points from each class as large as possible. This distance is called the margin. A larger margin usually means the classifier will work better on new data.

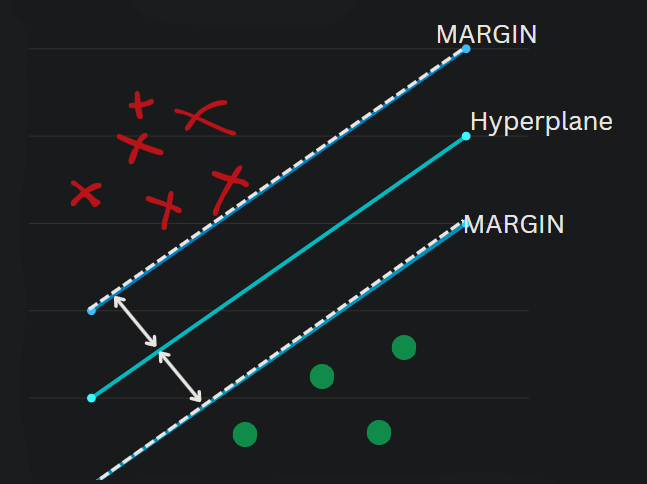
Red and Green are two separate classes with a hyperplane dividing those classes in such a way that the margin should be MAXIMUM.

Many hyperplanes can divide the classes in many different ways but the CHOSEN ONE IS THE ONE WITH MAXIMUM MARGIN DISTANCE. Talking in technical terms The core idea of an SVM is to solve an optimization problem. For a linearly separable dataset, the optimization problem can be formulated as:

• Objective: Maximize the margin.

• Constraints: Ensure that all data points are correctly classified.

Now you can see the similarity or you can relate your Lagrange multiplier with SVM

let's see how mathematically it goes, The goal of an SVM is to find the hyperplane that best separates different classes of data with the maximum margin. For a linearly separable dataset, we want to minimize the following objective function:

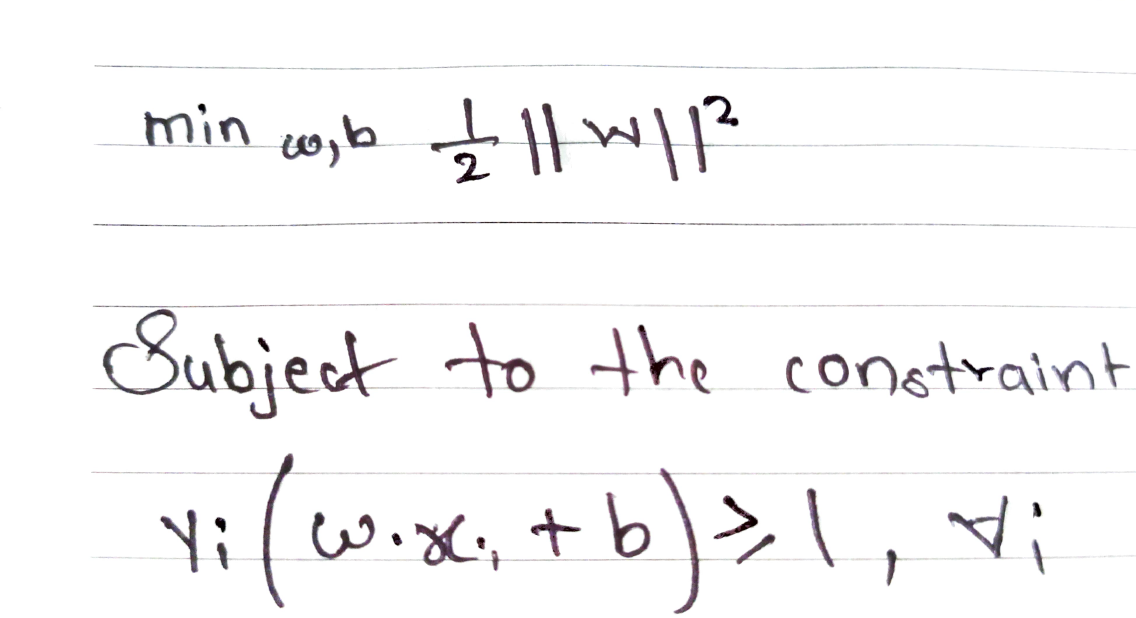
Here,

• w is the weight vector,

• b is the bias,

• xi​ are the feature vectors, and

• yi are the class labels.

Now somewhat you can relate to the above equation and the theoretical illustration regarding objectives and constraints.

The objective function 1/2 ||W||^2 is like balancing the workout. It tries to do two things at once:

1. Datapoints are correctly classified in a proper manner.

2. Keeping the margin maximum.

By making ||W|| as small as it can be.

This approach helps the model work better when it sees new data it hasn't been trained on

The constraints help to ensure that each data point i.e. xi is correctly classified. The label yi​ is either +1 or -1, which indicates the class of the corresponding data point xi.

Hope you will correlate Lagrange and SVM if you are going to learn in the upcoming Semester or have learned in the previous Semester this explanation would be really helpful to kind of motivate you to learn Machine Learning as well as your ongoing University Syllabus.

You never know what part of your daily life including the syllabus of the semester would help you solve complex problems of Machine Learning.