Understanding Depth-First Search
 Vineeth Chivukula
Vineeth ChivukulaDepth-First Search (DFS) is a traversal technique used in graph data structures that explores each branch as far as possible before backtracking. This technique is often implemented using a stack data structure or through recursion.
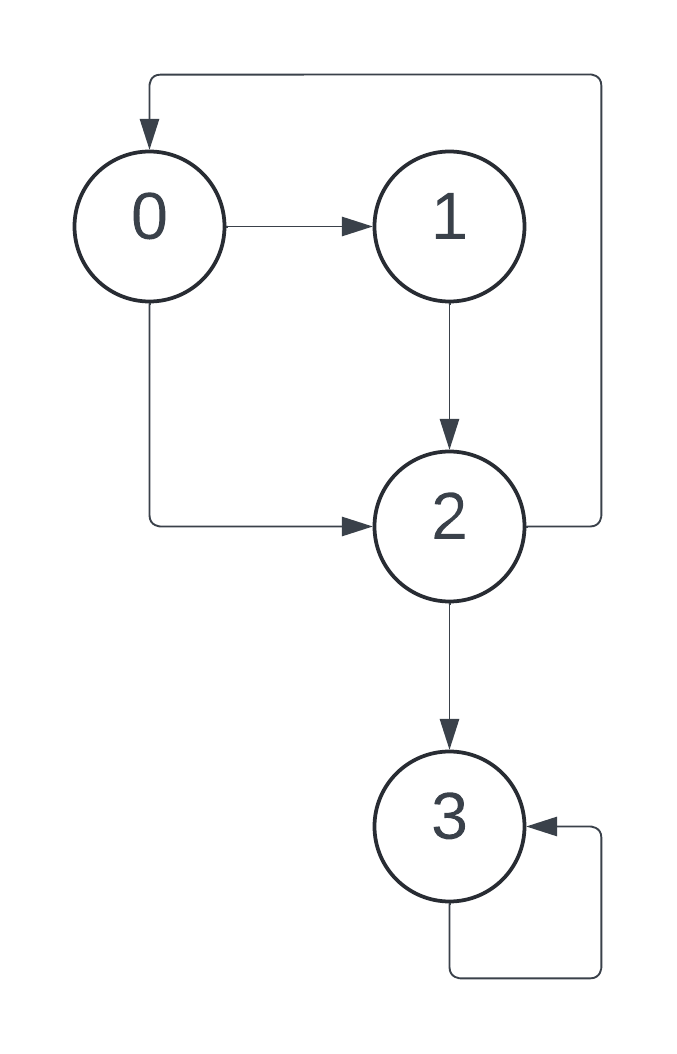
Process
Initialization: Initialize a stack (or use recursion) and push the starting vertex. Mark the starting vertex as visited.
Traversal: While the stack is not empty (or during the recursion), perform the following steps:
Pop the top vertex from the stack (or process the current vertex in recursion).
Process the vertex (e.g., print its value, check a condition, etc.).
Push all the adjacent (unvisited) vertices of the popped vertex onto the stack and mark them as visited.
Termination: The process terminates when the stack becomes empty, indicating that all vertices reachable from the starting vertex have been processed.
When to Use
Path Finding: To find a path between two vertices.
Connected Components: To check if a graph is connected or to find all the connected components in an undirected graph.
Topological Sorting: Order vertices in a Directed Acyclic Graph (DAG).
Cycle Detection: To detect cycles in both directed and undirected graphs.
Solving Puzzles: Useful in scenarios like mazes, puzzles, and games where all possible moves must be explored.
Time Complexity
The DFS traversal has a time complexity of O(V+E), where V is the number of vertices and E is the number of edges in the graph. This is because each vertex and each edge is processed exactly once.
Implementation using Recursion
// TC: O(V+E)
// SC: O(V)
import java.util.LinkedList;
class Graph {
private int V;
private LinkedList<Integer> adj[];
@SuppressWarnings({ "unchecked", "rawtypes" })
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; i++) {
adj[i] = new LinkedList();
}
}
void addEdge(int v, int w) {
adj[v].add(w);
}
void DFS(int s) {
boolean visited[] = new boolean[V];
DFSUtil(s, visited);
}
void DFSUtil(int s, boolean visited[]) {
visited[s] = true;
System.out.print(s + " ");
for (int n : adj[s]) {
if (!visited[n]) {
DFSUtil(n, visited);
}
}
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
g.DFS(2);
}
}
Implementation using Stack
// TC: O(V+E)
// SC: O(V)
import java.util.LinkedList;
import java.util.Stack;
class Graph {
private int V;
private LinkedList<Integer> adj[];
@SuppressWarnings({ "unchecked", "rawtypes" })
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; i++) {
adj[i] = new LinkedList();
}
}
void addEdge(int v, int w) {
adj[v].add(w);
}
void DFS(int s) {
boolean visited[] = new boolean[V];
Stack<Integer> stack = new Stack<>();
stack.push(s);
while (!stack.isEmpty()) {
int node = stack.pop();
if (!visited[node]) {
visited[node] = true;
System.out.print(node + " ");
for (int i = adj[node].size() - 1; i >= 0; i--) {
int n = adj[node].get(i);
if (!visited[n]) {
stack.push(n);
}
}
}
}
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
g.DFS(2);
}
}
Thank you for reading!
You can support me by buying me a book.
Subscribe to my newsletter
Read articles from Vineeth Chivukula directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Vineeth Chivukula
Vineeth Chivukula
There's this guy who's mad about editing and programming. It's his jam, you know?