Google’s Page Rank Algorithm

The history of Google as a search engine can be traced back to 1996, when “Larry Page” and “Sergey Brin” were PhD students at Stanford University. They were working on a project to develop a new way to rank web pages, and they came up with an algorithm called PageRank. PageRank works by analysing the links between web pages, and it assigns a higher ranking to pages that are linked to by many other pages.

In 1997, Page and Brin registered the domain name “google.com” and launched the first version of their search engine. The search engine was initially called BackRub, but it was renamed to “Google” in 1998. Google quickly became the most popular search engine in the world, and it has remained at the top ever since.

There are quite a few reasons why Google has been so successful. One of those reasons is the “PageRank Algorithm” which is very effective at ranking web pages.

Today, we will be diving deeper into the mechanics and the logic of how this brilliant algorithm works!

We will be looking into a simplification of the real “PageRank Algorithm”. Assume a situation where you have 3 friends named B, C and D with your name as A. You and your friends have 1 unit of power and you all can endorse this power to any of your friends except yourself.

A Graph representing the links between 2 or More Nodes

Case A: As we can see in the diagram, A decides to endorse B with all of the power he has. Therefore, B gets 1 unit of power from A.

Case B: B decides to endorse C and D, so they each get 0.5(equal distribution) units of power.

Case C: Similarly, C decides to endorse A and D with its power. Thus, A and D each get 0.5 units of power.

Case D: Lastly, D also gives 0.5 units of power to A and B.

We can now represent this graph in the form of a matrix where, each column of the matrix represents the outgoing arrows of power. Each row would represent the units of power it receives from its friends.

Lets make the matrix for the first column A.

Matrix(A)-

Matrix A

From the graph, we can notice that there is one outgoing power source from A to B, thus we can mark row B in column A to be 1 and the rest of them can be 0.

Following a similar approach for the other vertices we get,

Matrix(M)-

Matrix M

Note-

1. Some meaningful observations to make here are that each cell in the diagonal of the matrix will always be ‘0’ as one cannot link to itself.

Matrix A (Diagonals Highlighted)

2. Also, the sum of each column will always be 1 since each person had 1 unit of power to start with.

Matrix A (Sum of Each Column)

Now, we can assume A, B, C and D to be websites and the power they were sharing will be the outgoing links from their respective websites.

The intuitive approach to Rank these webpages now is to check the number of incoming links from all websites and then ranking the websites accordingly. Although the websites can be ranked this way, its highly inaccurate as it doesn’t take into account the probability of the user clicking on a particular website and we cannot differentiate between tied websites (in this case A and D).

Thus, to accurately find the way to rank these websites we consider probability which solves both of our problems.

To find these ranks we try to determine the answer to the following question, “If we spend a long time randomly clicking links assuming equal time intervals spent on each website, what percentage of time would be spent on each website?”

These percentages will be the rankings of each website,

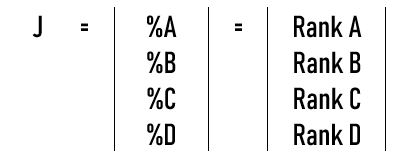
Matrix J

Let’s assume that our user searches for something and he/she gets 4 websites (in our case A, B, C and D).

Thus, the probability of the user clicking on each website initially will be-

P(A) = ¼ = 0.25

P(B) = ¼ = 0.25

P(C) = ¼ = 0.25

P(D) = ¼ = 0.25

Representing this probability as our initial rankings in Matrix (R0). Therefore,

Matrix R0 (Initial Probability)

To get the further probabilities, we simply multiply M by R0,

Therefore,

Matrix R1 (Probability After 1 Round of Clicks)

Similarly,

Therefore,

Matrix R1 (Probability After 2 Rounds of Clicks)

Repeating this process an infinite times(that is limit tending to infinity) we get,

Matrix J

Thus, Matrix J represents the ranking of each site.

Matrix J (With corresponding Ranks)

Thus visually, Website B will be ranked first, D will be second, A will be third and C will be fourth.

This calculation can be mathematically expressed as,

Mathematical Form of the PageRank Algorithm

FAQ- Why did Site D Rank higher than Site A at the end even when they each had 2 endorsements each?

Ans) Well the answer to this question lies in the rankings itself. Site D has received one of its endorsements from Site B which is the highest ranked website which is a quality assurance for the algorithm and thus it ranks D higher than A.

In our example, Websites A, B, C and D were the only websites accounted for, increase the number of websites and we can see how the complexity increases.

The PageRank algorithm is not the only factor that Google uses to rank search results. Other factors include the content of the page, the keywords used on the page, and the user’s location.

And without any doubt, the Google PageRank Algorithm is not so simple. The PageRank algorithm is a complex algorithm, and there is still much that is not known about how it works. Google has developed its algorithm throughout the years to stay ahead in the Search Engine Game but this is the simplified logic behind the scenes. The PageRank algorithm is constantly being updated and improved.

The PageRank algorithm is not the only factor that Google uses to rank search results. Other factors include the content of the page, the keywords used on the page, and the user’s location.

Hope you had a good time reading the article. I would be glad to talk to you about the same. Connect with me on LinkedIn , Github , Instagram and Twitter / X.