Backtest architecture

The FMZ platform backtest program is a complete control process, and the program is polling non-stop according to a certain frequency. The data returned by each market and trading API also simulates the actual running time according to the calling time. It belongs to the onTick level, not the onBar level of other backtest systems. Better support for backtest of strategies based on Ticker data (strategies with higher operating frequency).

The difference between simulation level backtest and real market level backtest

Simulation level backtest

The simulation level backtest is based on the bottom K-line data of the backtest system, and according to a certain algorithm, the ticker data interpolation is simulated within the framework of the values of the highest, lowest, opening, and closing prices of the given bottom K-line Bar into this Bar time series.

Real market level backtest

The real market level backtest is the real ticker level data in Bar's time series. For strategies based on ticker-level data, using real market level backtest is closer to reality. Backtest at the real market level, ticker is real recorded data, not simulated.

Simulation level backtest mechanism-bottom K line

There is no bottom K-line option for real market backtest (because ticker data is real, no bottom K-line is needed to simulate the generation).

In the simulation level backtest, the generated ticker is simulated based on the K-line data. This K-line data is the bottom K-line. In the actual use of simulation level backtest, the period of the bottom K line must be less than the period of calling the API to obtain the K line when the strategy is running. Otherwise, due to the large cycle of the bottom K line and insufficient number of generated tickers, the data will be distorted when calling the API to obtain the K line of the specified period. When using the large-period K-line backtest, you can appropriately increase the bottom K-line cycle.

How to generate ticker data for the bottom K line

The mechanism for generating simulated tickers on the bottom K line is the same as the famous trading software MetaTrader 4

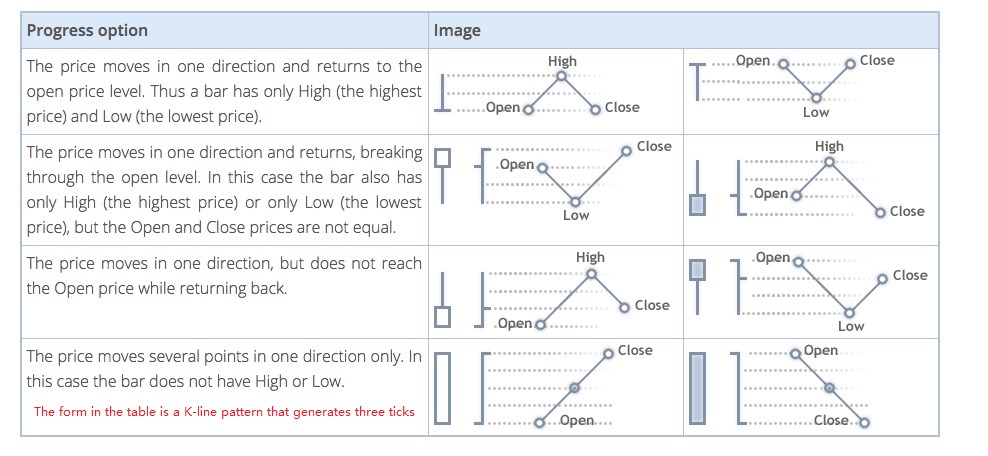
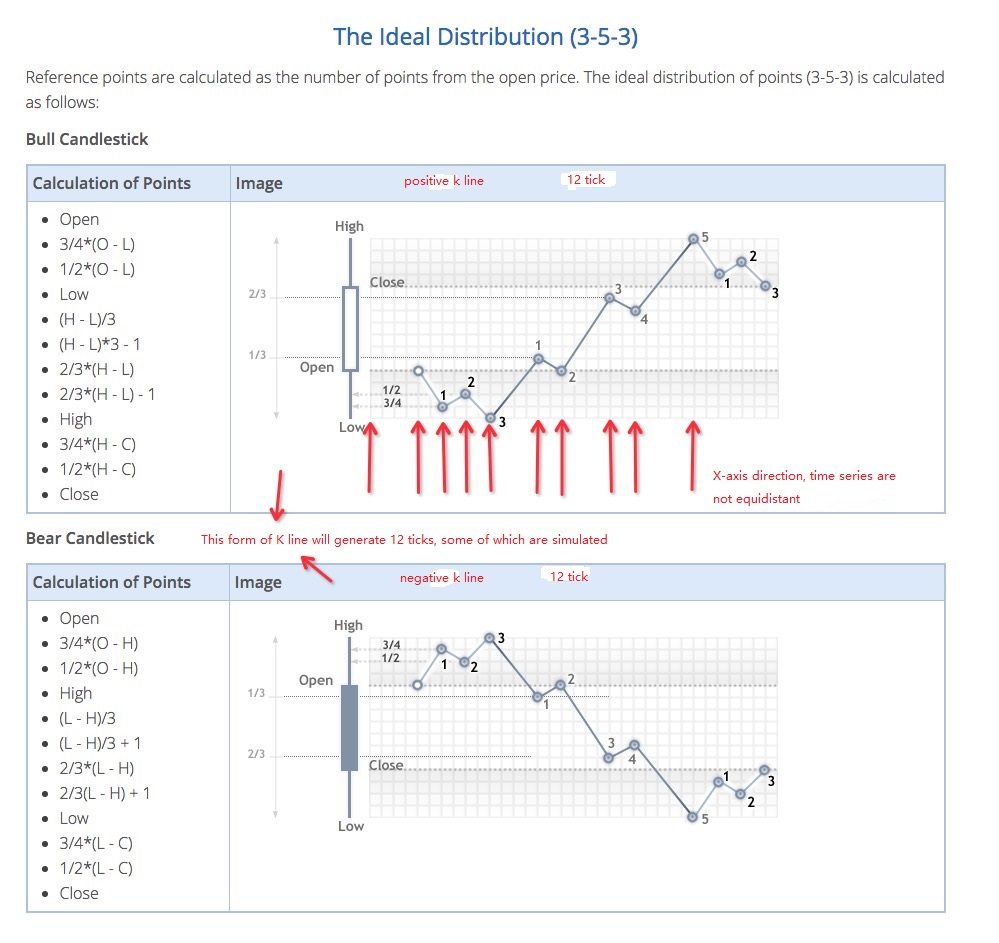
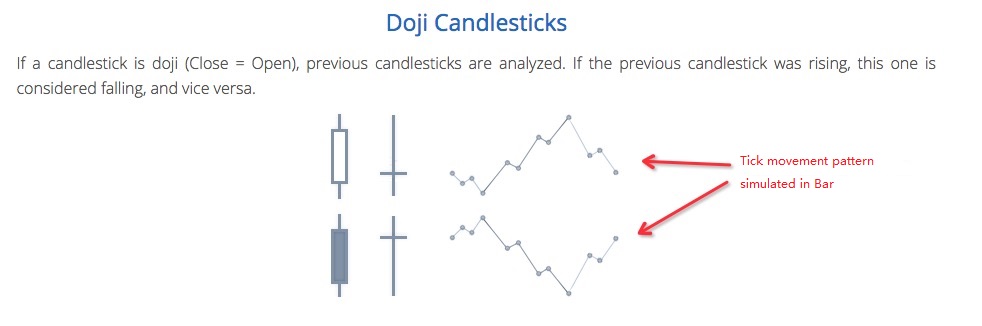
Algorithm code for generating ticker data

Specific algorithm for simulating tick data from the bottom K-line data:

function recordsToTicks(period, num_digits, records) {
    // http://www.metatrader5.com/en/terminal/help/tick_generation
    if (records.length == 0) {
        return []
    }
    var ticks = []
    var steps = [0, 2, 4, 6, 10, 12, 16, 18, 23, 25, 27, 29]
    var pown = Math.pow(10, num_digits)

    function pushTick(t, price, vol) {
        ticks.push([Math.floor(t), Math.floor(price * pown) / pown, vol])
    }

    for (var i = 0; i < records.length; i++) {
        var T = records[i][0]
        var O = records[i][1]
        var H = records[i][2]
        var L = records[i][3]
        var C = records[i][4]
        var V = records[i][5]
        if (V > 1) {
            V = V - 1
        }
        if ((O == H) && (L == C) && (H == L)) {
            pushTick(T, O, V)
        } else if (((O == H) && (L == C)) || ((O == L) && (H == C))) {
            pushTick(T, O, V)
        } else if ((O == C) && ((O == L) || (O == H))) {
            pushTick(T, O, V / 2)
            pushTick(T + (period / 2), (O == L ? H : L), V / 2)
        } else if ((C == H) || (C == L)) {
            pushTick(T, O, V / 2)
            pushTick(T + (period * 0.382), (C == L ? H : L), V / 2)
        } else if ((O == H) || (O == L)) {
            pushTick(T, O, V / 2)
            pushTick(T + (period * 0.618), (O == L ? H : L), V / 2)
        } else {
            var dots = []
            var amount = V / 11
            pushTick(T, O, amount)
            if (C > O) {
                dots = [
                    O - (O - L) * 0.75,
                    O - (O - L) * 0.5,
                    L,
                    L + (H - L) / 3.0,
                    L + (H - L) * (4 / 15.0),
                    H - (H - L) / 3.0,
                    H - (H - L) * (6 / 15.0),
                    H,
                    H - (H - C) * 0.75,
                    H - (H - C) * 0.5,
                ]
            } else {
                dots = [
                    O + (H - O) * 0.75,
                    O + (H - O) * 0.5,
                    H,
                    H - (H - L) / 3.0,
                    H - (H - L) * (4 / 15.0),
                    H - (H - L) * (2 / 3.0),
                    H - (H - L) * (9 / 15.0),
                    L,
                    L + (C - L) * 0.75,
                    L + (C - L) * 0.5,
                ]
            }
            for (var j = 0; j < dots.length; j++) {
                pushTick(T + period * (steps[j + 1] / 30.0), dots[j], amount)
            }
        }
        pushTick(T + (period * 0.98), C, 1)
    }
    return ticks
}

Therefore, when using the simulation level backtest, there will be price jumps in the time series.

From: FMZ simulation level backtest mechanism explanation

FMZ simulation level backtest mechanism explanation