TIL - pick's theorem
 Sammith S Bharadwaj
Sammith S Bharadwaj
So I was wondering about finding area of an irregular shape as I was googling and surfing through youtube I found pick's theorem.
This theorem provides a way to find area of a polygon in terms of integer points within it and and on the boundary:
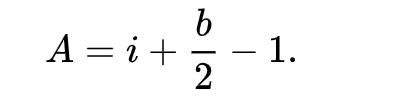
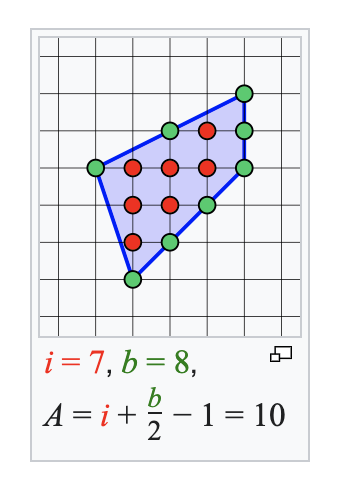
Imagining the polygon on a cartersian plane will simplify the process of finding the area of it. Of course there are proof to prove this, but I shall leave it as an exercise to you all as even I do not know lol. I read it and kinda understood it but not in the mood or have patience to really get into it and understand it, so I shall skip it. But what I am in mood for is a p5.js visualisation, my favourite viz tool.
let drawing = [];
let isDrawing = false;
let gridSpacing = 10;
function setup() {
createCanvas(600, 600);
background(255);
textSize(16);
noFill();
}
function draw() {
background(255);
drawGrid();
if (isDrawing) {
let point = createVector(mouseX, mouseY);
drawing.push(point);
}
stroke(0); // Set line color to black
strokeWeight(2);
beginShape();
for (let i = 0; i < drawing.length; i++) {
vertex(drawing[i].x, drawing[i].y);
fill(255, 0, 0);
ellipse(drawing[i].x, drawing[i].y, 5, 5); // Draw points
noFill();
}
endShape();
if (drawing.length > 2) {
let area = calculateArea(drawing);
fill(0);
noStroke();
text(`Area of Shape: ${area.toFixed(2)}`, 10, height - 40);
let totalArea = width * height;
text(`Total Canvas Area: ${totalArea}`, 10, height - 20);
noFill();
}
}
function mousePressed() {
isDrawing = true;
}
function mouseReleased() {
isDrawing = false;
}
function calculateArea(points) {
let boundaryPoints = 0;
let interiorPoints = 0;
for (let x = 0; x <= width; x += gridSpacing) {
for (let y = 0; y <= height; y += gridSpacing) {
let inside = isInside(x, y, points);
if (inside) {
interiorPoints++;
stroke(0, 255, 0);
} else {
stroke(255);
}
point(x, y);
}
}
for (let i = 0; i < points.length; i++) {
let x0 = points[i].x;
let y0 = points[i].y;
let x1 = points[(i + 1) % points.length].x;
let y1 = points[(i + 1) % points.length].y;
let dx = abs(x1 - x0);
let dy = abs(y1 - y0);
boundaryPoints += gcd(dx, dy);
}
interiorPoints -= boundaryPoints / 2;
let area = interiorPoints + boundaryPoints / 2 - 1;
return area * gridSpacing * gridSpacing;
}
function isInside(x, y, points) {
let crosses = 0;
for (let i = 0; i < points.length; i++) {
let x0 = points[i].x;
let y0 = points[i].y;
let x1 = points[(i + 1) % points.length].x;
let y1 = points[(i + 1) % points.length].y;
if (((y0 > y) !== (y1 > y)) && (x < (x1 - x0) * (y - y0) / (y1 - y0) + x0)) {
crosses++;
}
}
return crosses % 2 > 0;
}
function gcd(a, b) {
return b == 0 ? a : gcd(b, a % b);
}
function drawGrid() {
stroke(200);
strokeWeight(1);
for (let x = 0; x <= width; x += gridSpacing) {
line(x, 0, x, height);
}
for (let y = 0; y <= height; y += gridSpacing) {
line(0, y, width, y);
}
}
So more code than text in this article but that's fine I guess.
Subscribe to my newsletter
Read articles from Sammith S Bharadwaj directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
