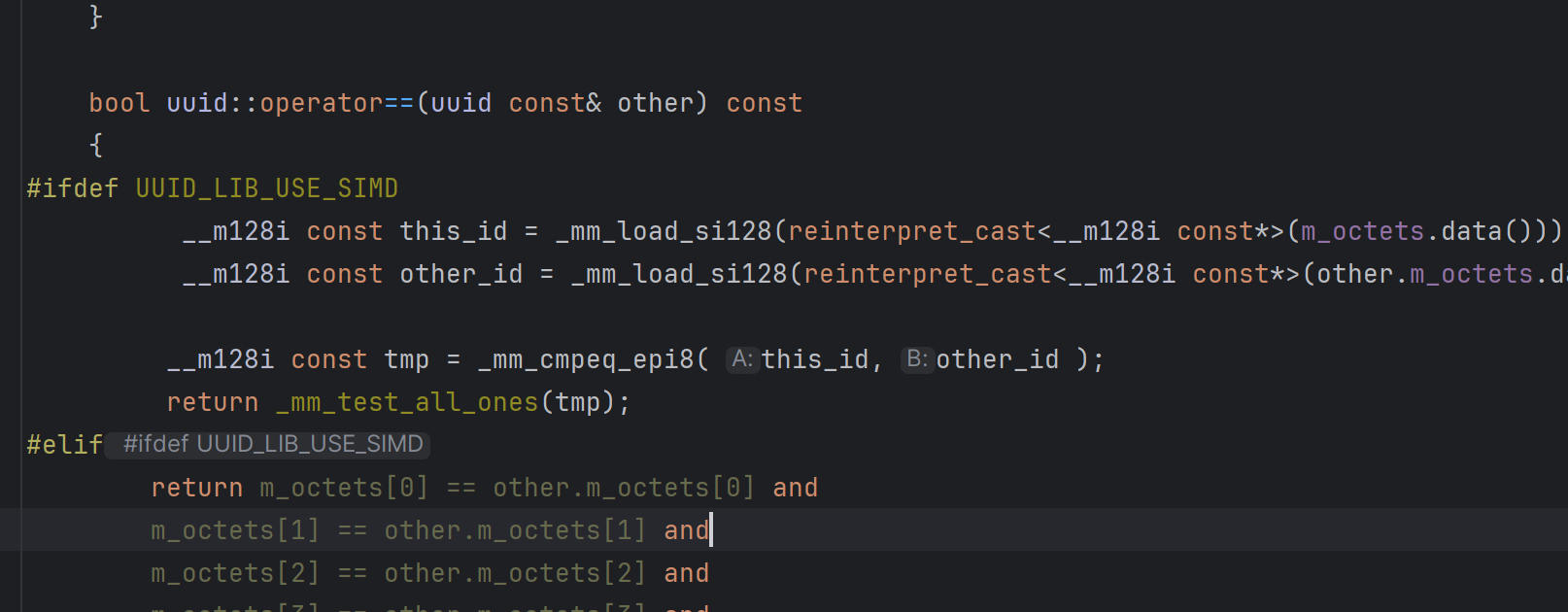
Introduction

Lately I've been experimenting with creating my own UUID/GUIDs in C++, mostly for my own learning, and it turned out to be a really good source for learning new things!

The UUIDs are based on RFC 9562 and the library includes functions to create both version 4 and version 7 UUIDs. UUID v4 is based on two random numbers whereas a v7 UUID is based on a Unix time stamp, a random number and an optional counter. The counter allows for sequential (monotonically increasing) UUIDs to be created.

Note that this project is solely for my own learning, not to display the best coding practices. Please don't use the code in the repo for production - there are other libraries for generating rfc9562-compliant uuids!

UUID in C++

There are a few ways we can model a UUID in C++. One way is to use integer members for the different sections of the UUID. The approach I took was to simply store everything as an array of 16 octets. This makes it straightforward to create UUIDs with more granular structure, for instance if you need to build version 6 UUIDs. User-defined UUIDs (v8) can also be created without restriction and still be compatible with "built-in" UUIDs. However there is currently only built-in support for v4 and v7.

The class interface looks like this:

struct uuid {
        explicit uuid();
        explicit constexpr uuid(std::array<uint8_t, 16> const &bytes);
        explicit uuid(uint8_t constant);

        bool operator==(const uuid &) const;
        bool operator<(const uuid &) const;

        [[nodiscard]] std::string as_string() const;
        [[nodiscard]] std::string as_string_braced() const;

        static const uuid nil;
        static const uuid max;

        alignas(16)
        std::array<uint8_t, 16> m_octets{};
    };

The uuid class exposes a few constructors for creating an empty UUID, creating one from a set of bytes or from a constant - filling all octets with the same value. We also expose two predefined values - uuid::nil and uuid::max - defined in the standard. as_string returns a string in the familiar format, with an optional member function to return a string enclosed in braces, which is seen on some systems (don't ask me why).

We have two comparison operators that allow the user of the library to check if two UUIDs are equal or if one is less than the other. Equality here is defined as bitwise equality - two UUIDs are equal iff all 128 bits are identical.

Finally we note that the class has an alignment requirement - alignas(16), but more on this later.

Equality Operator

By iterating coding and benchmarking, I came up with four different ways of writing the equality operator for my UUIDs. The benchmark results are provided below. For comparison the benchmarks for UUID v4 and v7 creation are also provided. Also the tests have been separated in two cases - tests with equal UUIDs and tests where the UUIDs are not equal - as some implementations have different results in the two cases.

Run on (16 X 3294 MHz CPU s)
CPU Caches:
  L1 Data 32 KiB (x8)
  L1 Instruction 32 KiB (x8)
  L2 Unified 512 KiB (x8)
  L3 Unified 16384 KiB (x1)
-----------------------------------------------------------------
Benchmark                       Time             CPU   Iterations
-----------------------------------------------------------------
BM_create_uuid_v4            6.49 ns         6.42 ns    112000000
BM_create_uuid_v7            46.1 ns         46.0 ns     14933333
(==) Simple Loop             8.03 ns         8.02 ns     89600000
(!=) Simple Loop             3.13 ns         3.08 ns    213333333
(==) Unrolled Loop           5.21 ns         5.16 ns    100000000
(!=) Unrolled Loop           3.11 ns         3.08 ns    213333333
(==) Unrolled Loop XOR       5.00 ns         5.08 ns    144516129
(!=) Unrolled Loop XOR       5.19 ns         5.16 ns    100000000
(==) SIMD                    1.81 ns         1.80 ns    373333333
(!=) SIMD                    1.91 ns         1.90 ns    344615385

(==) and (!=) SIMD have a standard deviation of 0.043 ns and 0.033 ns respectively. Remember, you can measure the standard deviation in benchmark by specifying ->Repetitions(x) when defining the benchmark. I used 100 repetitions, which may be a bit low but I don't have all day to wait for benchmarks. The other results have a standard deviation of roughly the same magnitude.

Simple Loop

My first take on the equality operator was something along the following lines:

bool uuid::operator==(uuid const& other) const
{
    for(uint8_t i = 0; i < 16; ++i)
    {
        if(m_octets[i] != other.m_octets[i]) return false;
    }

    return true;
}

Here we loop over all octets and return false as soon as we find one that does not match. If we manage to loop through all of them, then the two UUIDs must be equal. Clean and easy to understand code!

The problem with this approach is that there is a "penalty" for testing UUIDs that are equal, as we must then loop through all of the octets before we stop. The running time for non-equal UUIDs depends on when the operation is short-circuitied. Also, having an equality operator that is slower feels somewhat unsatisfying.

When running the Google benchmarks on my machine, it takes about 6 ns to create a v4 UUID. In comparison comparing two equal UUIDs takes about 8 ns. Comparing two UUIDs that are not equal depends on how many checks are needed before we detect the inequality, but it seems to be somewhere between 3-8 ns.

Unrolling the Loop

Can we improve this? Yes! It turns out that if I manually unroll the entire loop, I can shave off a few nanoseconds from the equality case:

bool uuid::operator==(uuid const& other) const
{
    return m_octets[0] == other.m_octets[0] and
        m_octets[1] == other.m_octets[1] and
        m_octets[2] == other.m_octets[2] and
        m_octets[3] == other.m_octets[3] and
        m_octets[4] == other.m_octets[4] and
        m_octets[5] == other.m_octets[5] and
        m_octets[6] == other.m_octets[6] and
        m_octets[7] == other.m_octets[7] and
        m_octets[8] == other.m_octets[8] and
        m_octets[9] == other.m_octets[9] and
        m_octets[10] == other.m_octets[10] and
        m_octets[11] == other.m_octets[11] and
        m_octets[12] == other.m_octets[12] and
        m_octets[13] == other.m_octets[13] and
        m_octets[14] == other.m_octets[14] and
        m_octets[15] == other.m_octets[15];
}

This looks horrible, but takes somewhere between 3-5 ns on my machine - so a saving of 3 ns in the worst case. This is great!

Another thing we can try is to observe that if a and b are equal, then a bitwise xor will return 0. Thus, another rather ugly unrolled loop-variant might look like this:

bool uuid::operator==(uuid const& other) const
{
    return 0 == (m_octets[0] ^ other.m_octets[0]) |
        (m_octets[1] ^ other.m_octets[1]) |
        (m_octets[2] ^ other.m_octets[2]) |
        (m_octets[3] ^ other.m_octets[3]) |
        (m_octets[4] ^ other.m_octets[4]) |
        (m_octets[5] ^ other.m_octets[5]) |
        (m_octets[6] ^ other.m_octets[6]) |
        (m_octets[7] ^ other.m_octets[7]) |
        (m_octets[8] ^ other.m_octets[8]) |
        (m_octets[9] ^ other.m_octets[9]) |
        (m_octets[10] ^ other.m_octets[10]) |
        (m_octets[11] ^ other.m_octets[11]) |
        (m_octets[12] ^ other.m_octets[12]) |
        (m_octets[13] ^ other.m_octets[13]) |
        (m_octets[14] ^ other.m_octets[14]) |
        (m_octets[15] ^ other.m_octets[15]);
}

This has the advantage that there is no difference between the equal and non-equal cases. On my machine both cases run in about 5 ns, so we are now down to the same running time as creating a new v4 UUID - great! But we can actually do even better.

Using SIMD

The last attempt I came up with was to manually vectorize the code using compiler intrinsics, which also seems to give the best results, at least on my machine and given the way the benchmarks are written.

bool uuid::operator==(uuid const& other) const
{
      __m128i const this_id = _mm_load_si128(reinterpret_cast<__m128i const*>(m_octets.data()));
      __m128i const other_id = _mm_load_si128(reinterpret_cast<__m128i const*>(other.m_octets.data()));

     __m128i const tmp = _mm_cmpeq_epi8( this_id, other_id );
     return _mm_test_all_ones(tmp);
}

SIMD stands for "Single Instruction Multiple Data" and allows us to apply the same operation to a number of operands. We can e.g., add or multiply many numbers with the same constant in one instruction. Since our UUIDs consist of 16 octets, we can use SIMD instructions that operate on 128 bit values.

SIMD is a set of special assembly instructions, but we don't need to inline any assembly code - instead we can use the compiler intrinsics available from the meta header file immintrin.h. In c++26 we will also get std::simd, today available in the namespace std::experimental, but in this article I will only use compiler intrinsics.

To compare two UUIDs we must first load them into two of the special registers that are available for this instruction set. This can be done using the function _mm_load_si128 which loads some data into a 128 bit register. Referring to the reference documentation - Intel® Intrinsics Guide - we can see that the data has to be aligned on a 16-byte boundary, hence the alignas(16) declaration in the class that we saw earlier. If we don't do this the function will cause a segmentation fault, but it is also possible to use a load function that doesn't require aligned memory.

Having loaded the two UUIDs into memory, we can compare them using the function _mm_cmpeq_epi8. The manual tells us that this function compares packed 8-bit integers, and retuns either 0xFF or 0 for each integer. Thus, if the two UUIDs are equal, we will get a return value conisting of only 1's - 128 of them. If we were to loop over this array and compare each octet we would be back to square one, so how can we efficiently check if all bits are set?

Luckily there is another instruction we can use to check if all bits are set to 1 - _mm_test_all_ones. _mm_test_all_ones will compute a bitwise not of the data, and then perform a bitwise and with a 128-bit vector of only 1's. If the result is 0 the function returns 1, else it returns 0. See the corresponding entry in the intrinsics guide.

So if the two UUIDs are equal, we will get a 128-bit vector of only 1's from the first operation, then the second operation will return 1 which is then converted to a true. In the benchmarks on my machine this seems to be the fastest, running slightly less than 2 for both cases.

CMake Parameters

So now we have some nice SIMD instructions that make our equality operator blazingly fast, but how do we know that the SIMD instructions are available on the machine they are built on (for)? If you build this library on e.g. your toaster, SIMD instructions may not be recognized by the hardware, so we need a way to turn them on or off and fall back to the unrolled loop variant (which was faster than the "clean" loop).

However, on Windows it seems to be slightly annoying to detect if the CPU supports the instructions, and since we want the library to be platform agnostic(-ish) I simply define a preprocessor macro that can be used to turn on and off the usage of SIMD - so the burden is placed on the user of the library, who hopefully best knows the target hardware 😎

#ifdef UUID_LIB_USE_SIMD
          __m128i const this_id = _mm_load_si128(reinterpret_cast<__m128i const*>(m_octets.data()));
          __m128i const other_id = _mm_load_si128(reinterpret_cast<__m128i const*>(other.m_octets.data()));

         __m128i const tmp = _mm_cmpeq_epi8( this_id, other_id );
         return _mm_test_all_ones(tmp);
#elif
        ... // unrolled loop here
#endif

It would be nice if I could turn this on or off without touching the source code - and it turns out we can! After reading some CMake documentation and Stack Overflow, I found out that you can define a parameter for your CMake file like this:

set(UUID_LIB_USE_SIMDI 1 CACHE BOOL "Enable SIMD instructions if available on the target hardware")

I can set this from the command line if I want to:

cmake -DUUID_LIB_USE_SIMDI:BOOL=0

I also learned that I can define a preprocessor macro from CMake:

if(UUID_LIB_USE_SIMDI)
    MESSAGE("Adding SIMD support")
    add_compile_definitions(UUID_LIB_USE_SIMD)
    if ("${CMAKE_CXX_COMPILER_ID}" STREQUAL "Clang" OR "${CMAKE_CXX_COMPILER_ID}" STREQUAL "GNU")
        MESSAGE("Clang or GCC: Adding compiler flags for using simd intrinsics")
        set(CMAKE_CXX_FLAGS  "${CMAKE_CXX_FLAGS} -march=native")
    endif()
endif()

The last part adds the flag -march=native to the compiler if clang or gcc is being used to compile. This is required to use the SIMD instructions.

Conclusion

In this post I showed how I implemented the == operator for my UUID library. The purpose is to document my own learning process, not to show off the cleanest code or most clever architecture. There are probably many mistakes here, and if you find one or if you have a general reaction, feel free to leave a comment :)

That's all for today! I will try to follow up with an implementation of the < operator - when it's done.

What I learned from this project:

Reading a standard and implementing
Basics of using SIMD compiler intrinsics
Using Google Benchmark
Really useful CMake features, setting parameters from command line and defining preprocessor macros

I will revisit this implementation when std::simd becomes available with c++26 and do another benchmark.

Learning SIMD in C++

Table of contents