Data Structures - Java: Syntax, Use Case, Time and Space Complexity

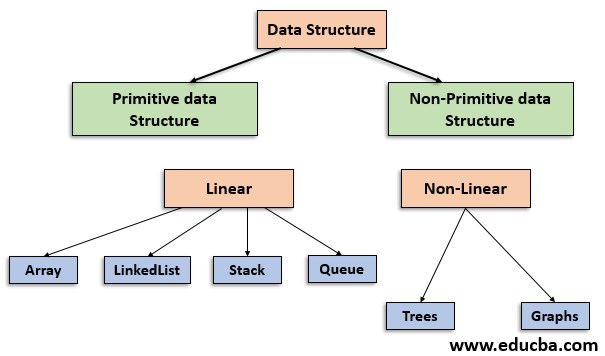
1. Arrays

Syntax:

// Declaration and initialization
int[] array = new int[10];
int[] array = {1, 2, 3, 4, 5};

// Accessing elements
int element = array[0];

// Modifying elements
array[1] = 10;

Use Cases: Fixed-size collections, fast access by index.

Time Complexity:

• Access: O(1)

• Search: O(n)

• Insertion: O(n) (for shifting elements)

• Deletion: O(n) (for shifting elements)

Space Complexity: O(n)

2. Linked Lists

Syntax:

class Node {
    int data;
    Node next;
    Node(int d) { data = d; next = null; }
}

class LinkedList {
    Node head;
    // Methods to add, remove, and traverse
}

Use Cases: Dynamic size collections, ease of insertion/deletion.

Time Complexity:

• Access: O(n)

• Search: O(n)

• Insertion: O(1)

• Deletion: O(1)

Space Complexity: O(n)

3. Stacks

Syntax:

Stack<Integer> stack = new Stack<>();
stack.push(1);
int element = stack.pop();

Use Cases: LIFO (Last In, First Out) operations, backtracking algorithms.

Time Complexity:

• Push: O(1)

• Pop: O(1)

• Peek: O(1)

Space Complexity: O(n)

4. Queues

Syntax:

Queue<Integer> queue = new LinkedList<>();
queue.add(1);
int element = queue.remove();

Use Cases: FIFO (First In, First Out) operations, scheduling algorithms.

Time Complexity:

• Enqueue: O(1)

• Dequeue: O(1)

• Peek: O(1)

Space Complexity: O(n)

5. Hash Tables (HashMap)

Syntax:

HashMap<Integer, String> map = new HashMap<>();
map.put(1, "One");
String value = map.get(1);

Use Cases: Fast key-value pair lookups, associative arrays.

Time Complexity:

• Insertion: O(1)

• Deletion: O(1)

• Search: O(1)

Space Complexity: O(n)

6. Trees

Syntax:

class TreeNode {
    int data;
    TreeNode left, right;
    TreeNode(int item) {
        data = item;
        left = right = null;
    }
}

Use Cases: Hierarchical data structures, searching and sorting (e.g., Binary Search Tree).

Time Complexity:

• Access/Search: O(log n) (for balanced trees)

• Insertion: O(log n) (for balanced trees)

• Deletion: O(log n) (for balanced trees)

Space Complexity: O(n)

7. Heaps

Syntax:

PriorityQueue<Integer> heap = new PriorityQueue<>();
heap.add(1);
int min = heap.poll();

Use Cases: Priority queue operations, heap sort.

Time Complexity:

• Insertion: O(log n)

• Deletion: O(log n)

• Find Min/Max: O(1)

Space Complexity: O(n)

8. Graphs

Syntax:

class Graph {
    private int V;
    private LinkedList<Integer> adj[];
    Graph(int v) {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }
}

Use Cases: Network representations, shortest path algorithms.

Time Complexity:

• Varies based on representation (Adjacency Matrix or List) and operation.

• BFS/DFS: O(V + E)

Space Complexity:

• Adjacency Matrix: O(V^2)

• Adjacency List: O(V + E)

By starting with these data structures, you will have a solid foundation for understanding their implementation, usage scenarios, and performance characteristics, which is crucial for effective algorithm development.