DSA Week 2 - II Non-Linear Data Structures Explained: A Beginner's Guide
 ritiksharmaaa
ritiksharmaaa
Non-Linear Data Structure
Non-linear data structures are those in which data elements are not arranged in a sequential order. Instead, they are organized in a hierarchical or interconnected manner, allowing more complex relationships among the data elements. Non-linear data structures are essential for representing relationships and hierarchies in various domains such as computer networks, databases, and artificial intelligence.
Key Non-Linear Data Structures
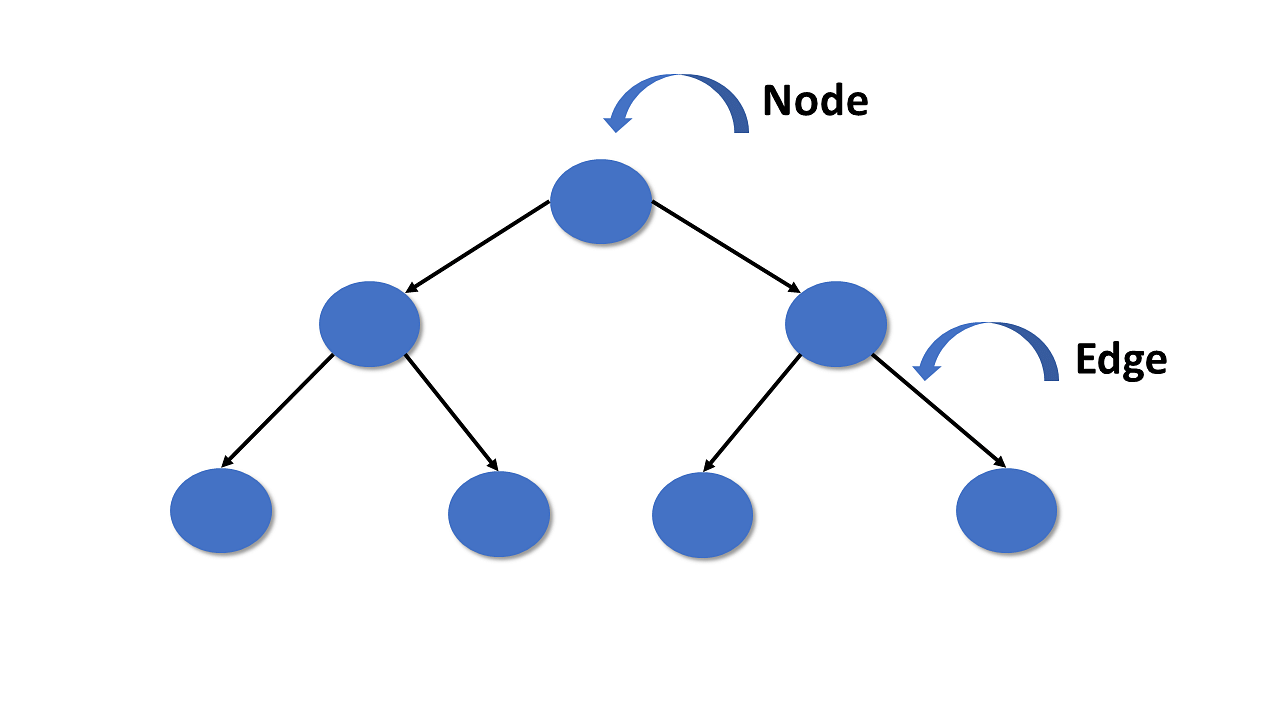
Trees
A tree is a hierarchical structure consisting of nodes, with one node as the root and others as its children. Each node can have zero or more child nodes.
Characteristics:
Root: The topmost node.
Parent: A node that has child nodes.
Child: A node that has a parent node.
Leaf: A node with no children.
Depth: The length of the path from the root to a node.
Height: The length of the path from a node to the deepest leaf.
Types of Trees:
Binary Tree: Each node has at most two children (left and right).
Binary Search Tree (BST): A binary tree where the left child contains values less than the parent node, and the right child contains values greater than the parent node.
AVL Tree: A self-balancing binary search tree where the difference in heights of left and right subtrees is at most one.
Heap: A special tree-based data structure that satisfies the heap property. It can be a max heap or a min heap.
Trie: A tree-like data structure used to store associative data structures.
Python Example of a Binary Tree:
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def inorder_traversal(root):
if root:
inorder_traversal(root.left)
print(root.value, end=' ')
inorder_traversal(root.right)
# Create nodes
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
# Inorder traversal
inorder_traversal(root) # Output: 4 2 5 1 3
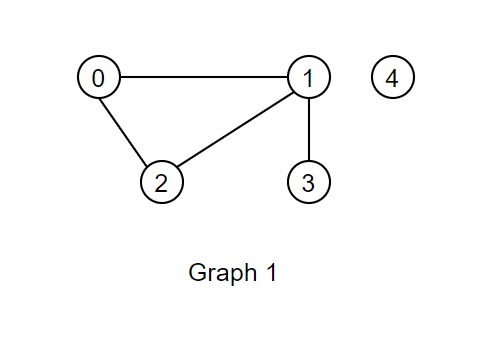
Graphs
A graph is a collection of nodes (vertices) connected by edges. Graphs can represent various systems such as social networks, transportation networks, and dependency structures.
Characteristics:
Vertex (Node): Fundamental unit of a graph.
Edge (Link): Connection between two vertices.
Directed Graph (Digraph): A graph where edges have a direction.
Undirected Graph: A graph where edges do not have a direction.
Weighted Graph: A graph where edges have weights representing cost, distance, or any metric.
Unweighted Graph: A graph where edges do not have weights.
Types of Graphs:
Adjacency Matrix: A 2D array where a cell represents the presence or absence of an edge between vertices.
Adjacency List: An array of lists where each list represents the neighbors of a vertex.
Python Example of a Graph Using Adjacency List:
class Graph:
def __init__(self):
self.graph = {}
def add_edge(self, u, v):
if u not in self.graph:
self.graph[u] = []
self.graph[u].append(v)
def print_graph(self):
for vertex in self.graph:
print(f"{vertex} -> {', '.join(map(str, self.graph[vertex]))}")
g = Graph()
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.add_edge(3, 3)
g.print_graph()
# Output:
# 0 -> 1, 2
# 1 -> 2
# 2 -> 0, 3
# 3 -> 3
Applications of Non-Linear Data Structures
Trees:
Binary Search Trees: Used in searching and sorting algorithms, such as in databases for indexing.
Heaps: Used in priority queues, graph algorithms like Dijkstra's algorithm, and in heap sort.
Tries: Used in dictionary implementations, spell checkers, and autocomplete features.
Graphs:
Social Networks: Representing relationships between users.
Transport Networks: Modeling routes and connections in transportation systems.
Web Crawling: Representing links between web pages.
Dependency Graphs: Managing project dependencies in build systems and package managers.
Understanding and efficiently utilizing non-linear data structures are crucial for solving complex problems and designing efficient algorithms in various domains.
UseCase Of This Data Structure
Trees:
Hierarchical data structure with a root and hierarchical relationships.
Useful in representing hierarchical data (file systems, organizational structures), implementing search algorithms (binary search trees), and balancing data (AVL trees, Red-Black trees).
Graphs:
Non-linear data structure composed of nodes and edges.
Used in representing networks (social networks, transportation networks), routing algorithms (shortest path), and dependency management.
These data structures cater to various computational needs, offering different trade-offs in terms of efficiency, flexibility, and ease of implementation depending on the specific use case and requirements of the application.
Subscribe to my newsletter
Read articles from ritiksharmaaa directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

ritiksharmaaa
ritiksharmaaa
Hy this is me Ritik sharma . i am software developer