How to choose the best Regression Model for your Data ?
 rajneel chougule
rajneel chougule
What are Regression Models? Regression models are techniques used to analyze the Independent variables also called features and Dependent variables called outcomes. These models are widely used in various fields for prediction, forecasting, and understanding the factors that influence a particular outcome.
Purpose of regression analysis:
Predict outcomes
Identify relationships between variables
Quantify the strength of those relationships
Core components:
Dependent variable (Y): The outcome we want to predict or explain
Independent variables (X): The factors we think can influence the dependent variable
Regression equation: Describes how Y changes with X
Types of Regression Models in ML:
Linear Regression:
Assumes a linear relationship between features and target
Polynomial Regression:
Extends linear regression to capture non-linear relationships
Ridge Regression (L2 regularization):
Useful when dealing with multicollinearity
Lasso Regression (L1 regularization):
Performs feature selection by shrinking less important feature coefficients to zero
Elastic Net:
Combines L1 and L2 regularization
Decision Tree Regression:
Can capture non-linear relationships
Random Forest Regression:
Reduces overfitting and improves generalization
Support Vector Regression (SVR):
Uses support vector machines for regression tasks
Neural Network Regression:
Uses artificial neural networks to model complex relationships
These are the types of Regression models that exist and are effective in their own specific way.
When to use which model is the question. DATA is the answer. Understanding your data is a crucial step in choosing the right regression model. Your data defines your model. Let's see what type of data is suitable for what type of model.
Type of Data: Simple, linear relationships between features and target
Linear Regression is used for such data
Example: House prices vs. single feature like square foot
Works well when relationships are approximately linear
Type of Data: Binary or categorical outcomes
Logistic Regression is used here.
Example: Predicting whether a customer will make a purchase. Yes pr No.
Works well when you need to predict probabilities of discrete outcomes

Type of Data: Non-linear, but smooth relationships
Polynomial Regression is applied.
Example: Plant growth over time
Works well when relationships follow a clear curved pattern

Type of Data: Many correlated features.
Ridge Regression is applied.
Example: Gene expression data with many related genes
Works well when you want to keep all features but reduce their impact
Risk of overfitting
Type of Data: Complex relationships, mix of feature types
Decision tree Regression is used
Examples: Predicting car prices based on various categorical and numerical features
Works well when relationships are non-linear and involve interactions

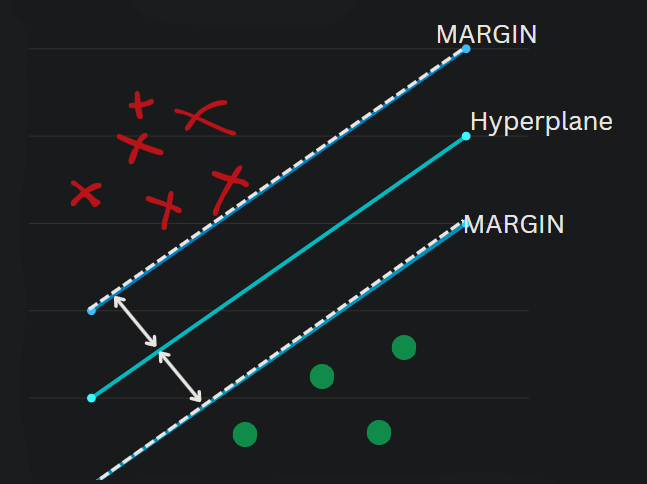
Type of Data : High-dimensional data, potentially with outliers
Support Vector Regression can be used here
Example: Financial time series prediction
Works well when you have a complex dataset and want to avoid overfitting.
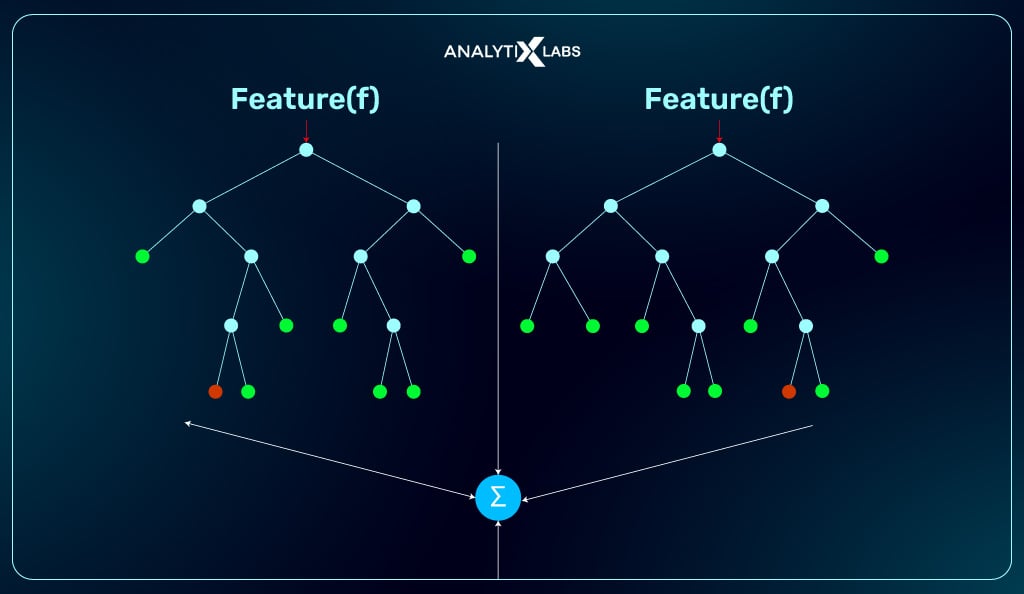
Type of Data: Complex, potentially noisy data with many features
Random Forest Regression is used.
Example: Environmental data to predict the crop yields
works well when you need reliable and stable predictions and can continue without getting a proper explanation of its decision.
Type of Data: Large, complex datasets with intricate patterns
Neural Network Regression is used.
Example: Image-based price prediction (e.g., house prices from photos)
Works well when you have a lot of data and relationships are highly non-linear
You can go through my Neural Network From Scratch GitHub repo
Covered most of the Regression models along with the type of required or you can say potentially suitable data for the models.
As we've explored the various regression models and their ideal data types it's clear that choosing the right model is crucial for accurate and meaningful results. From the simplicity of linear regression to the complexity of neural networks, each model has its strengths and ideal use cases.
As you approach your next data analysis project, consider these factors:
What's the nature of your data?
What's your primary goal – prediction, interpretation, or a balance of both?
What level of complexity can you manage in your model?
What did you learn from this Blog ?
Ultimately, regression analysis is both an art and a science. It requires not only technical knowledge but also intuition developed through experience. Don't be afraid to experiment with different models validate your results rigorously, and always stay curious about new developments in the field.
Subscribe to my newsletter
Read articles from rajneel chougule directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
