Exploring Kruskal's Algorithm in Java

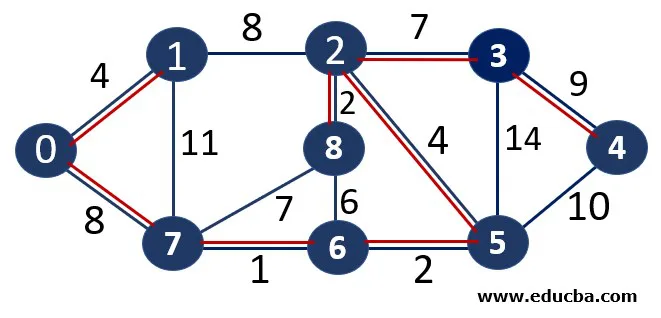
Introduction

Graph algorithms are a cornerstone of computer science, providing the tools necessary to solve many practical problems, such as network design, circuit design, and much more. Among these algorithms, Kruskal's Algorithm stands out for its efficiency in finding the Minimum Spanning Tree (MST) of a graph. In this blog post, we will dive deep into Kruskal's Algorithm, understand its applications, and implement it step-by-step in Java.

What is Kruskal's Algorithm?

Kruskal's Algorithm is a greedy algorithm that finds the MST for a connected weighted graph. The MST is a subset of the edges that connects all the vertices together, without any cycles and with the minimum possible total edge weight. This algorithm was developed by Joseph Kruskal in 1956 and has since become a fundamental part of graph theory.

Why Minimum Spanning Trees?

The concept of a Minimum Spanning Tree is essential in various fields, such as:

Network Design: Designing least-cost network paths.
Circuit Design: Reducing the total wiring length.
Clustering: Grouping data points in machine learning.

Steps of Kruskal's Algorithm

1. Sort all the edges in non-decreasing order of their weight.

2. Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If it doesn’t, add it to the MST. If it does, discard it.

3. Repeat step 2 until there are (V-1) edges in the MST (where (V) is the number of vertices).

Explanation

Sorting Edges: The first step involves sorting all the edges in ascending order based on their weights. This ensures that we can efficiently pick the smallest edge in each step.
Union-Find Data Structure: To detect cycles efficiently, we use the union-find data structure. This helps in keeping track of the components (subsets) and ensures no cycles are formed when adding an edge.
Building the MST: We iterate through the sorted edges, adding the smallest edge to the MST if it doesn’t form a cycle. This process continues until we have \( V-1 \) edges in the MST.

Implementation in Java

Let's dive into the Java implementation of Kruskal’s Algorithm.

Step 1: Define the Edge and Subset Classes

class Edge implements Comparable<Edge> {

    int src, dest, weight;

    public int compareTo(Edge compareEdge) {

        return this.weight - compareEdge.weight;

    }

}

class Subset {

    int parent, rank;

}

Edge Class: Represents an edge with source, destination, and weight. It implements Comparable to allow sorting based on weight.
Subset Class: Helps manage the unin-find operations for detecting cycles.

Step 2: Define the KruskalAlgorithm Class

public class KruskalAlgorithm {

    int V, E;    // Number of vertices and edges

    Edge[] edge; // Array to store all edges

    KruskalAlgorithm(int v, int e) {

        V = v;

        E = e;

        edge = new Edge[E];

        for (int i = 0; i < e; ++i) {

            edge[i] = new Edge();

        }

    }

    int find(Subset[] subsets, int i) {

        if (subsets[i].parent != i)

            subsets[i].parent = find(subsets, subsets[i].parent);

        return subsets[i].parent;

    }

    void union(Subset[] subsets, int x, int y) {

        int xroot = find(subsets, x);

        int yroot = find(subsets, y);

        if (subsets[xroot].rank < subsets[yroot].rank)

            subsets[xroot].parent = yroot;

        else if (subsets[xroot].rank > subsets[yroot].rank)

            subsets[yroot].parent = xroot;

        else {

            subsets[yroot].parent = xroot;

            subsets[xroot].rank++;

        }

    }

    void kruskalMST() {

        Edge[] result = new Edge[V];

        int e = 0; // Index variable for result[]

        int i = 0; // Index variable for sorted edges

        for (i = 0; i < V; ++i)

            result[i] = new Edge();

        // Step 1: Sort all the edges in non-decreasing order of their weight.

        Arrays.sort(edge);

        // Allocate memory for creating V subsets

        Subset[] subsets = new Subset[V];

        for (i = 0; i < V; ++i)

            subsets[i] = new Subset();

        // Create V subsets with single elements

        for (int v = 0; v < V; ++v) {

            subsets[v].parent = v;

            subsets[v].rank = 0;

        }

        i = 0; // Index used to pick the next edge

        // Number of edges to be taken is equal to V-1

        while (e < V - 1) {

            // Step 2: Pick the smallest edge. Check if it forms a cycle with the spanning tree

            // formed so far. If cycle is not formed, include this edge. Else, discard it.

            Edge next_edge = edge[i++];

            int x = find(subsets, next_edge.src);

            int y = find(subsets, next_edge.dest);

            if (x != y) {

                result[e++] = next_edge;

                union(subsets, x, y);

            }

        }

        // Print the constructed MST

        System.out.println("Following are the edges in the constructed MST:");

        for (i = 0; i < e; ++i)

            System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);

    }

    public static void main(String[] args) {

        int V = 4; // Number of vertices in graph

        int E = 5; // Number of edges in graph

        KruskalAlgorithm graph = new KruskalAlgorithm(V, E);

        // add edge 0-1

        graph.edge[0].src = 0;

        graph.edge[0].dest = 1;

        graph.edge[0].weight = 10;

        // add edge 0-2

        graph.edge[1].src = 0;

        graph.edge[1].dest = 2;

        graph.edge[1].weight = 6;

        // add edge 0-3

        graph.edge[2].src = 0;

        graph.edge[2].dest = 3;

        graph.edge[2].weight = 5;

        // add edge 1-3

        graph.edge[3].src = 1;

        graph.edge[3].dest = 3;

        graph.edge[3].weight = 15;

        // add edge 2-3

        graph.edge[4].src = 2;

        graph.edge[4].dest = 3;

        graph.edge[4].weight = 4;

        graph.kruskalMST();

    }

}

Explanation of the Code

Initialization: The KruskalAlgorithm class initializes the graph with vertices and edges. Each edge is stored in an array of Edge objects.
Find Operation: The find method uses path compression to find the root of a subset, helping in efficient cycle detection.
Union Operation: The `union` method merges two subsets using union by rank to keep the tree flat.
Kruskal's MST: The kruskalMST method implements the main logic. It sorts the edges, iteratively picks the smallest edge, and adds it to the MST if it doesn’t form a cycle.
Main Method: The main method sets up the graph with vertices and edges, then calls kruskalMST to construct and print the MST.

Conclusion

Kruskal's Algorithm is a powerful and efficient way to find the MST of a graph. By using a greedy approach and the union-find data structure, it ensures that the resultant MST has the minimum possible weight. The Java implementation provided here is a straightforward and effective way to understand and apply Kruskal's Algorithm to real-world problems.

Feel free to share your thoughts or ask questions in the comments below. Happy coding!

I hope this more detailed version meets your needs! Let me know if there are any other adjustments or additions you'd like.

Understanding Kruskal's Algorithm with Java

Table of contents