The following code is my very first implementation of Binary Search in Java (which returns the index of the target element in the array):

public static int binarySearch(int[] arr, int target) {
    int start = 0;
    int end = arr.length - 1;
    int middle;

    while (start <= end) {
        middle = (start + end) / 2;
        if (arr[middle] == target) {
            return middle;
        } else if (target > arr[middle]) {
            start = middle + 1;
        } else {
            end = middle - 1;
        }
    }

    return -1;
}

Although it might seem that the code should work (and it actually does in most cases), there is a 'hidden' bug that can cause failures under certain conditions.

How Binary Search works

Binary Search is a searching algorithm used in a sorted array. Instead of starting the search at index 0, we find the middle element and compare it with our target value. If the target value is larger, we can discard the first half of the array - we have halved the search interval. Then we find the middle element of our search interval and we repeat the process. We continue this way until we find the target element or until the search interval is empty.

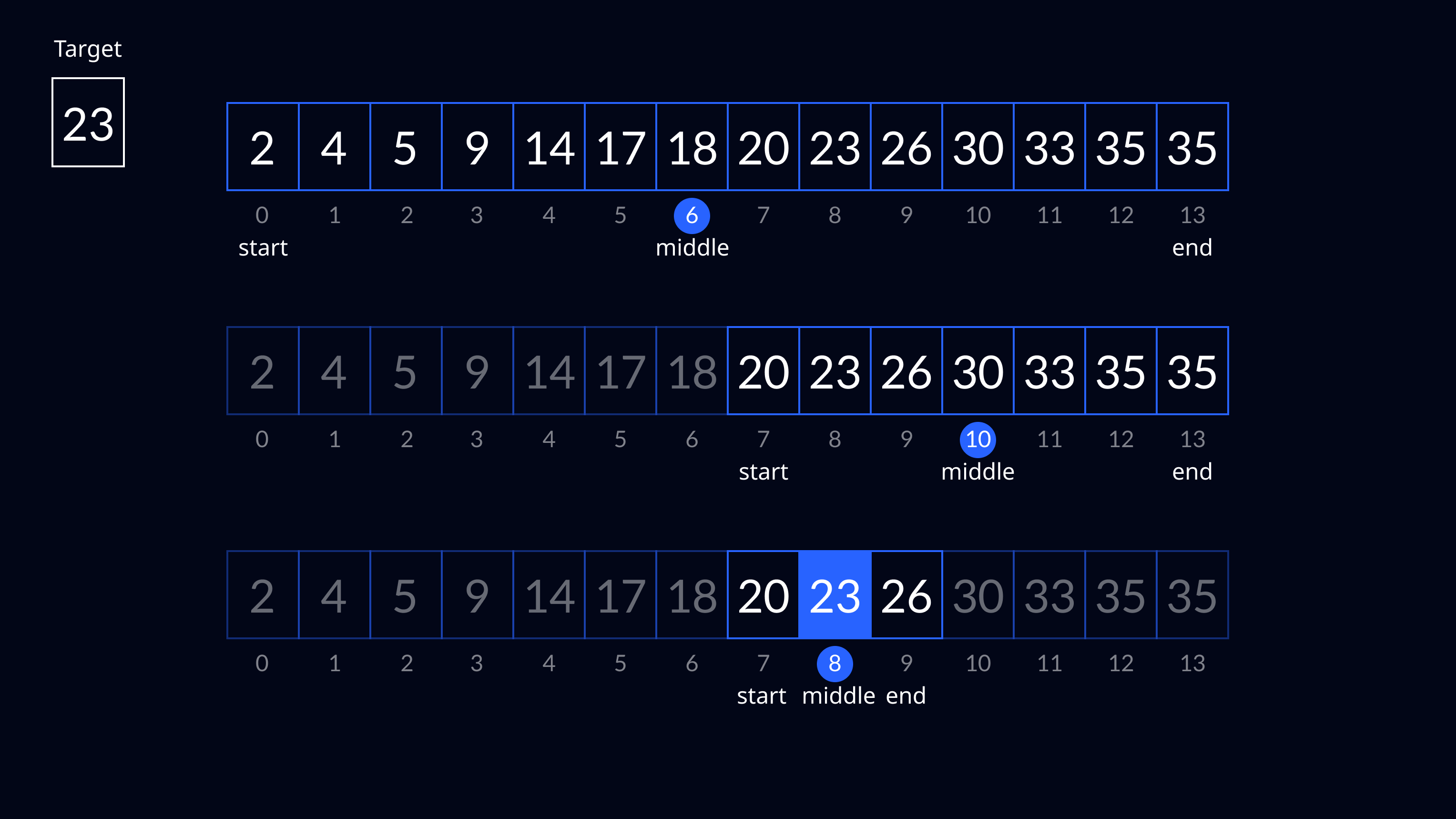
Finding the middle element

So, how exactly do we find the middle element of the search interval? I went with the most obvious method of finding the middle element - simply adding the start and end indices of the search interval and dividing the result by 2 (basically taking the average of the two numbers).

middle = (start + end) / 2

Even though this makes sense, in some cases, it will cause the Binary Search to fail. But before we discuss why, we first have to talk about how integers are stored in memory.

How are numbers stored in Java

In Java, an integer is stored as a 32-bit two's complement. As I mentioned in my previous post about representing negative numbers in binary, using a signed two's complement representation allows us to store both positive and negative numbers. The range of values we can store is given by the number of available bits. If we have $x$ bits, the smallest number we can represent is $(-1)\cdot 2^{x-1}$ and the largest number is $2^{x-1}-1$.

For simplicity, let's say we are working with 4 bits. We can represent numbers from -8 to 7.

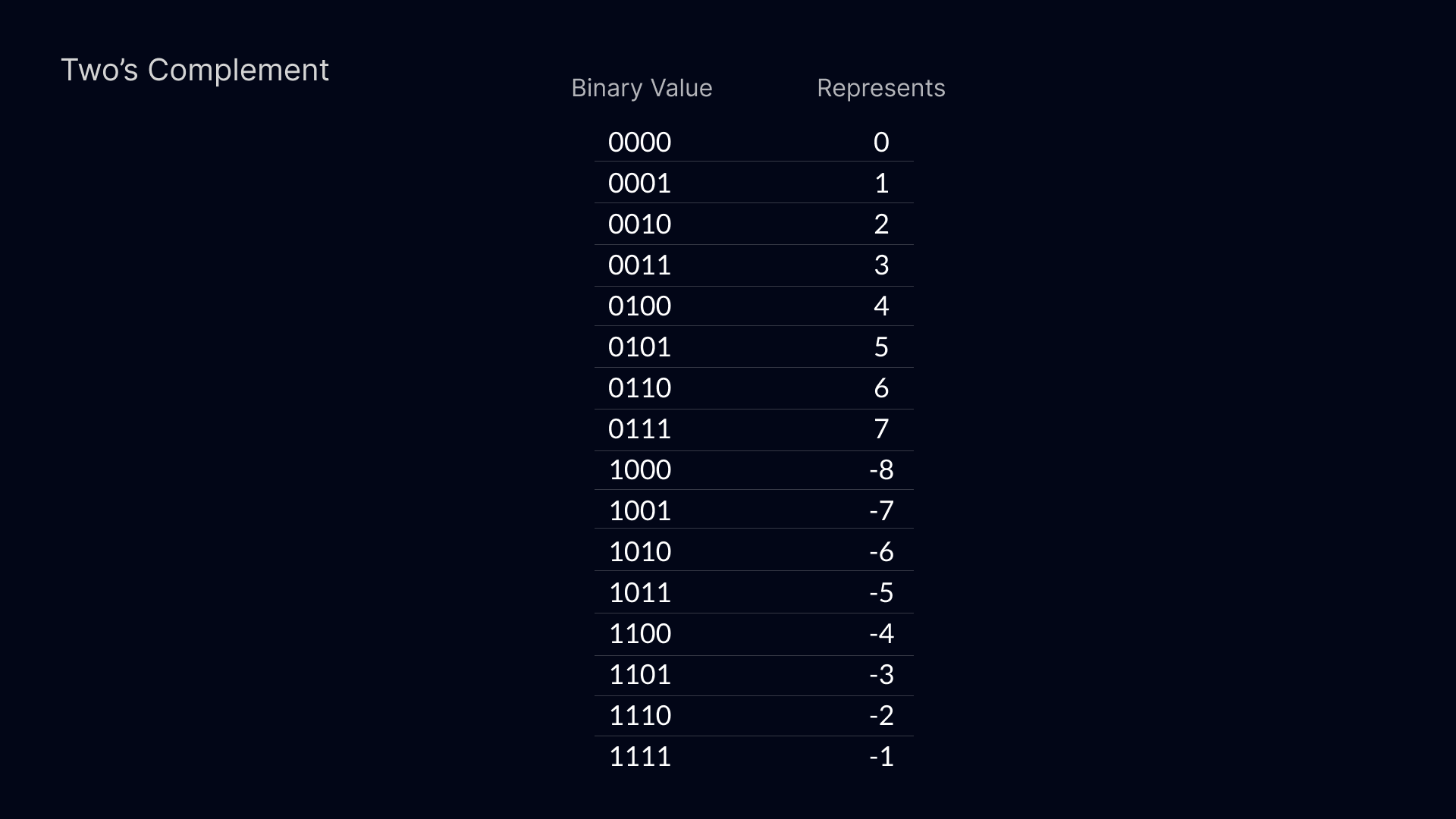
But what happens if we exceed this range of values? Let's say I want to add 1 to 7. This should give us 8, but that's out of our range! If the value exceeds the maximum value, we call it an overflow.

If we ask a computer to add two numbers it will add them and return whatever result it gets without much thinking. Let's pretend we are a computer and add 1 and 7 in binary.

We got 1000, which is 8 in binary, but because we agreed on representing numbers as two's complement, it actually represents -8! We can check that by converting 1000 (representing a two's complement) to decimal as we did in my previous post:

When adding two positive numbers using two's complement, we CAN get a negative number, because when we exceed our range of possible values, we "wrap around" at the other side.

This works exactly the same in Java. Only instead of 4 bits, we use 32 bits. The range of possible values is from -2147483648 ($(-1)\cdot 2^{31}$) to 2147483647 ($2^{31}-1$).

Overflow🚨

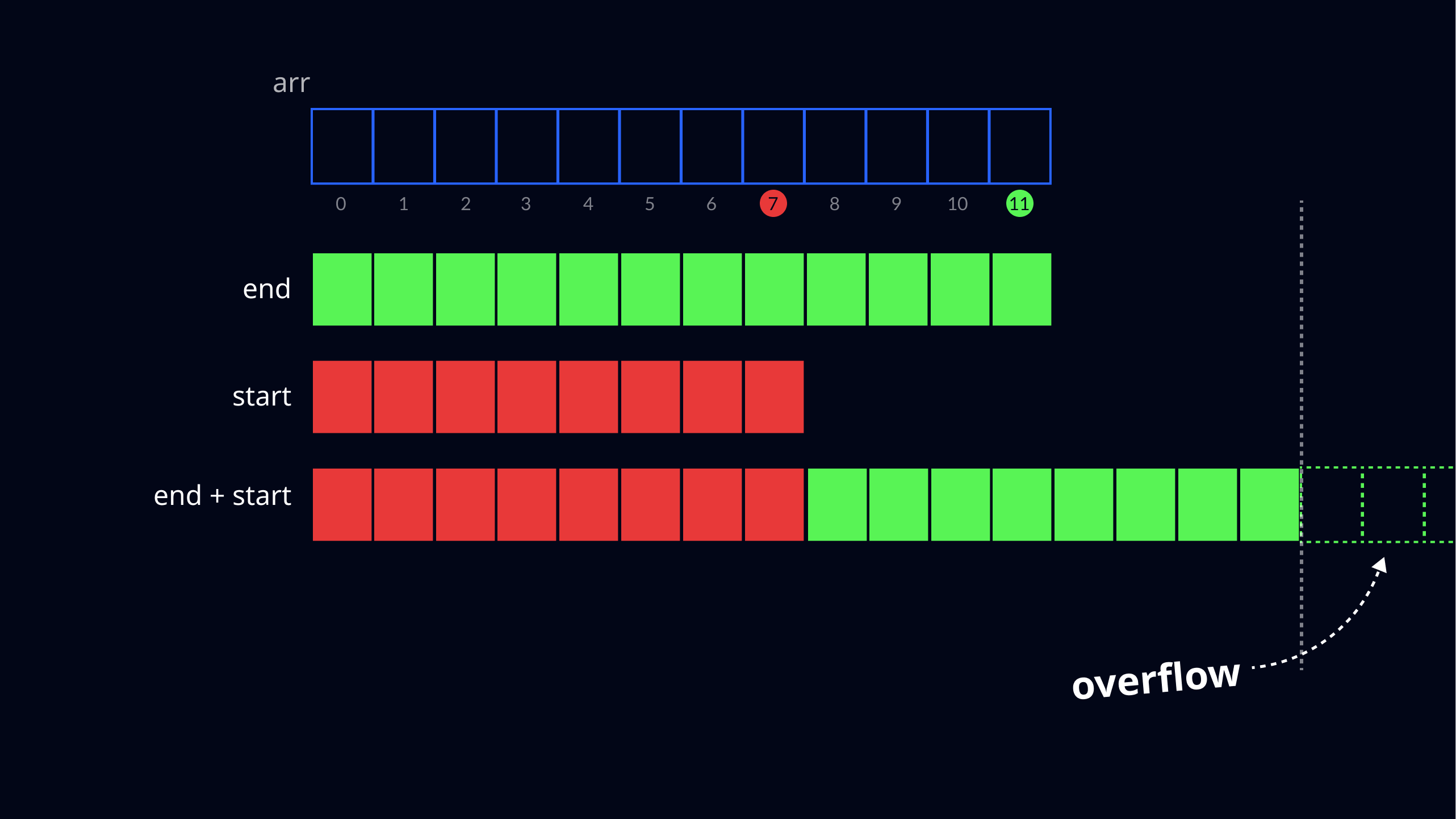
You may have already spotted the potential error in finding the middle element using the "intuitive" approach I used in my Binary Search. Let's imagine we are working for a big tech company that's dealing with a lot of data. We were asked to write a Binary Search for finding elements in a sorted array. This array has around 1.5 billion elements. Well, let's see how I would do. First, my algorithm would find the index of the middle, which is 750,000,000 - no problem there.

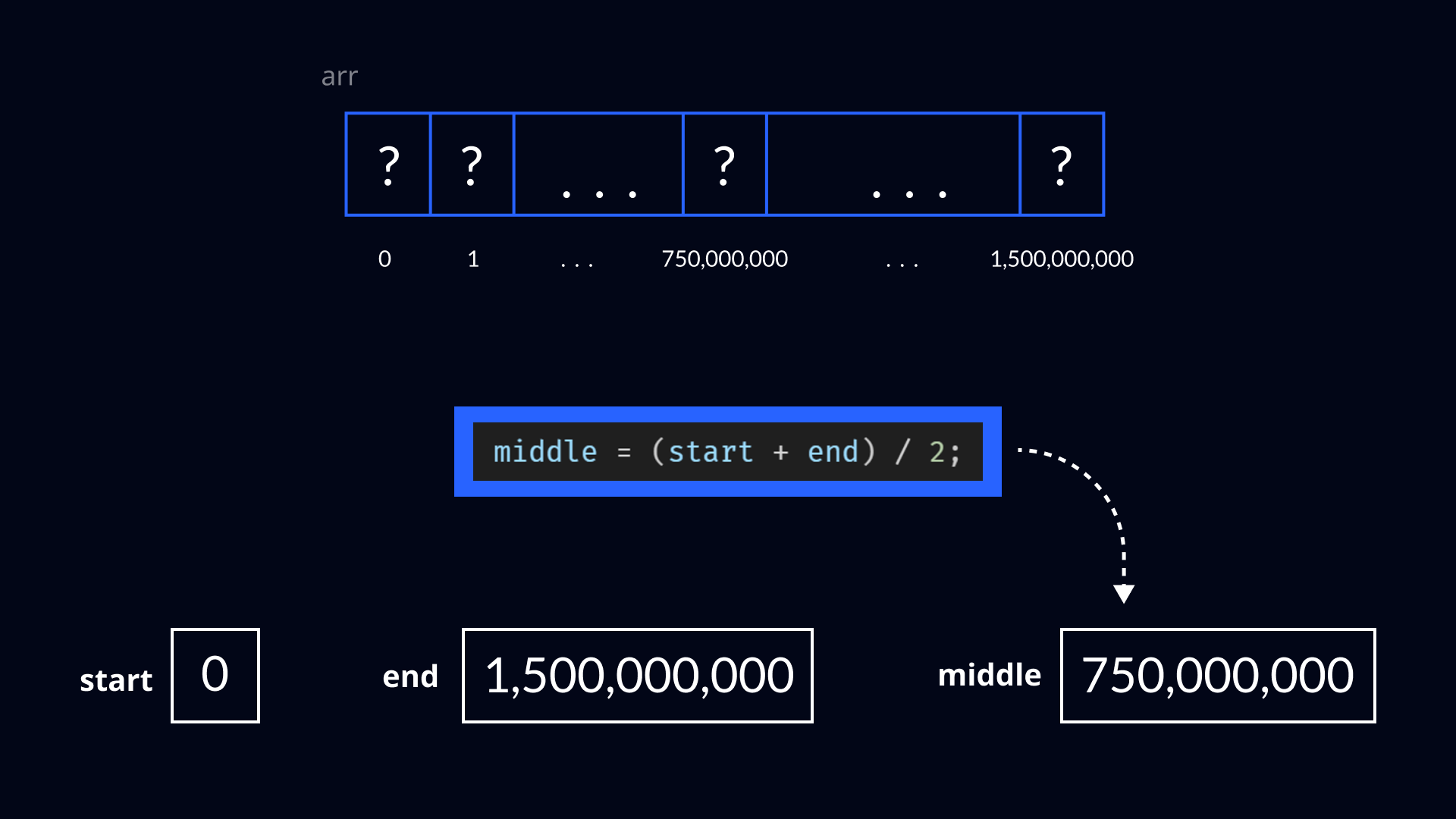
It would compare the value of the middle element with the target value. The target value is larger, so it must be in the second half of the array - I can discard the first half and reduce the searching interval to the second half.

Now let's repeat the process by finding the index of the new middle element in the searching interval.

Then we have to compare the value of the middle element with the target value. Let's access the middle element by its index to get its value and... we get java.lang.ArrayIndexOutOfBoundsException. But how could we get this exception? The middle index should be 1,125,000,000, which is in our range of possible indices (from 0 to arr.length -1).

If we would try to access the new middle element of the array by hardcoding the index (arr[1125000000]), we would get the value with no problem. But according to the exception, we are trying to access an element that doesn't exist (in other words, the index is out of the range of possible indices).

The problem lies in the intermediate calculation when we add the start and end indices together. In this case, when we add them together we get 2,250,000,001. But this number exceeds the largest number we can store as an integer in Java. So the sum "wraps around" and becomes a large negative number. When we then divide it by 2, we get -1,022,483,647. We are getting the "array index out of bounds exception" because we are trying to access an element with a negative index (which definitely isn't in the range of possible indices).

When should we get worried

Out of curiosity, let's determine the maximum length of an array on which we could use my implementation of Binary Search without worrying about overflow. Let's say our array is of length $x$. What is the largest sum we can get? Well the largest sum we can get is when the target is the last element of the array, which has an index of $x-1$. In that case, both start and end will have a value of $x-1$ so when we add them together we get $2x-2$. We know that this value has to be less or equal to the largest number we can represent as int ($2^{31}-1$).

$$\begin{align} 2^{31}-1&\le 2x-2 \\ 2^{31}+1&\le 2x \\ \frac{2^{31}+1}{2}&\le x \\ 1073741824.5&\le x \end{align}$$

So if our array has less than 1,073,741,825 elements, even my code will work as intended. But that doesn't mean I should leave my code as it is (knowing the potential risk) and only assume it will never be used on any larger array. So how can we deal with the overflow?

How to fix it🤔

The first option could be to use more bits to represent numbers. If we used a long instead of int, the above example would work just fine (and I probably wouldn't get fired from the tech company). In Java, long stores numbers as 64-bit two's complement, which means that the largest number we can represent is 9,223,372,036,854,775,807 ($2^{63}-1$). Although this might seem sufficient, as the size of the array gets closer to this number, we would face the same problem.

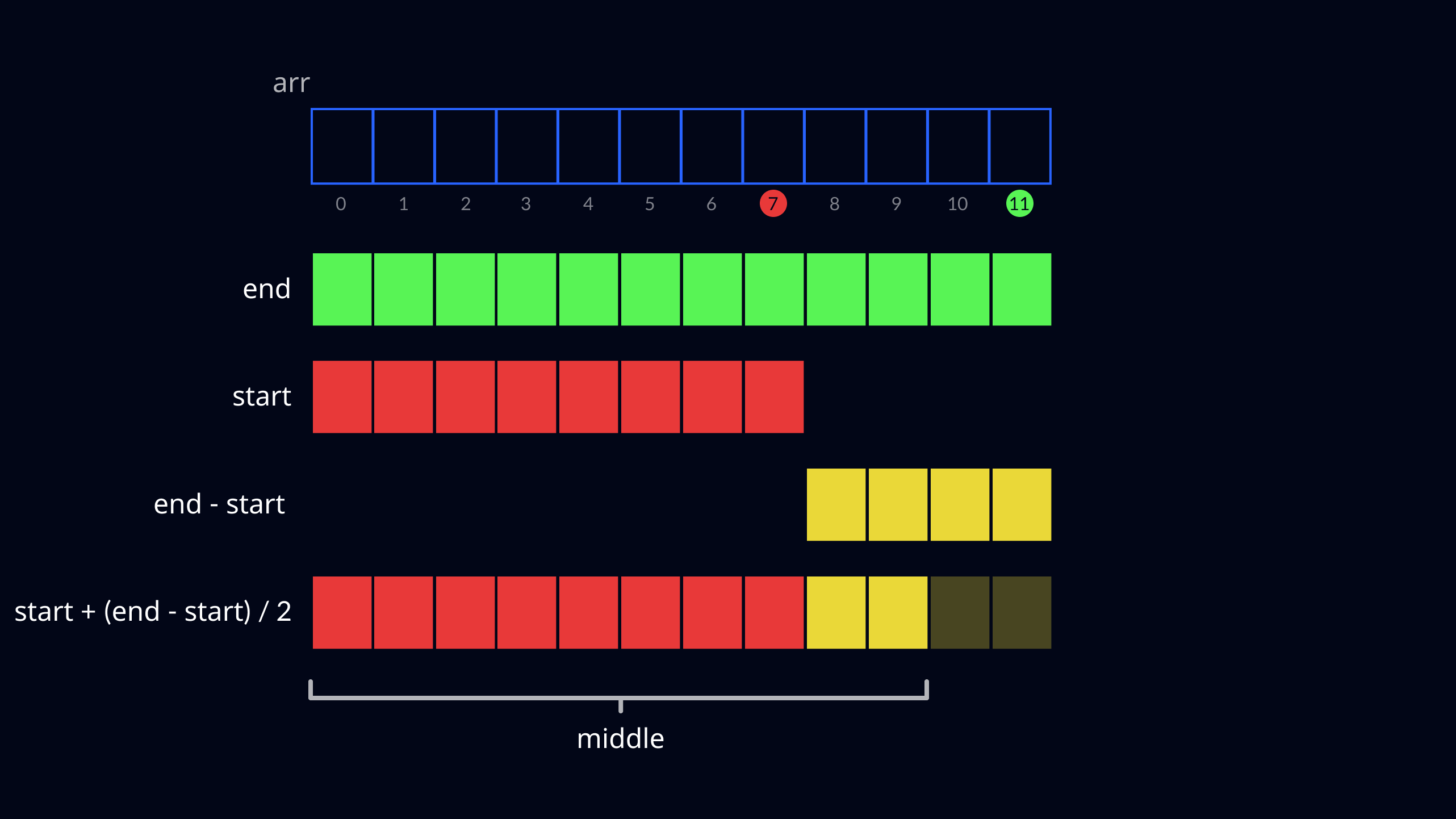
A better solution is to use a different method for finding the index of the middle element. If you search for Binary Search online, the method for finding the index will probably look something like this:

middle = start + (end - start) / 2

We can check that the value that gets stored in the middle variable is the same as when using my "intuitive" method for finding the middle index:

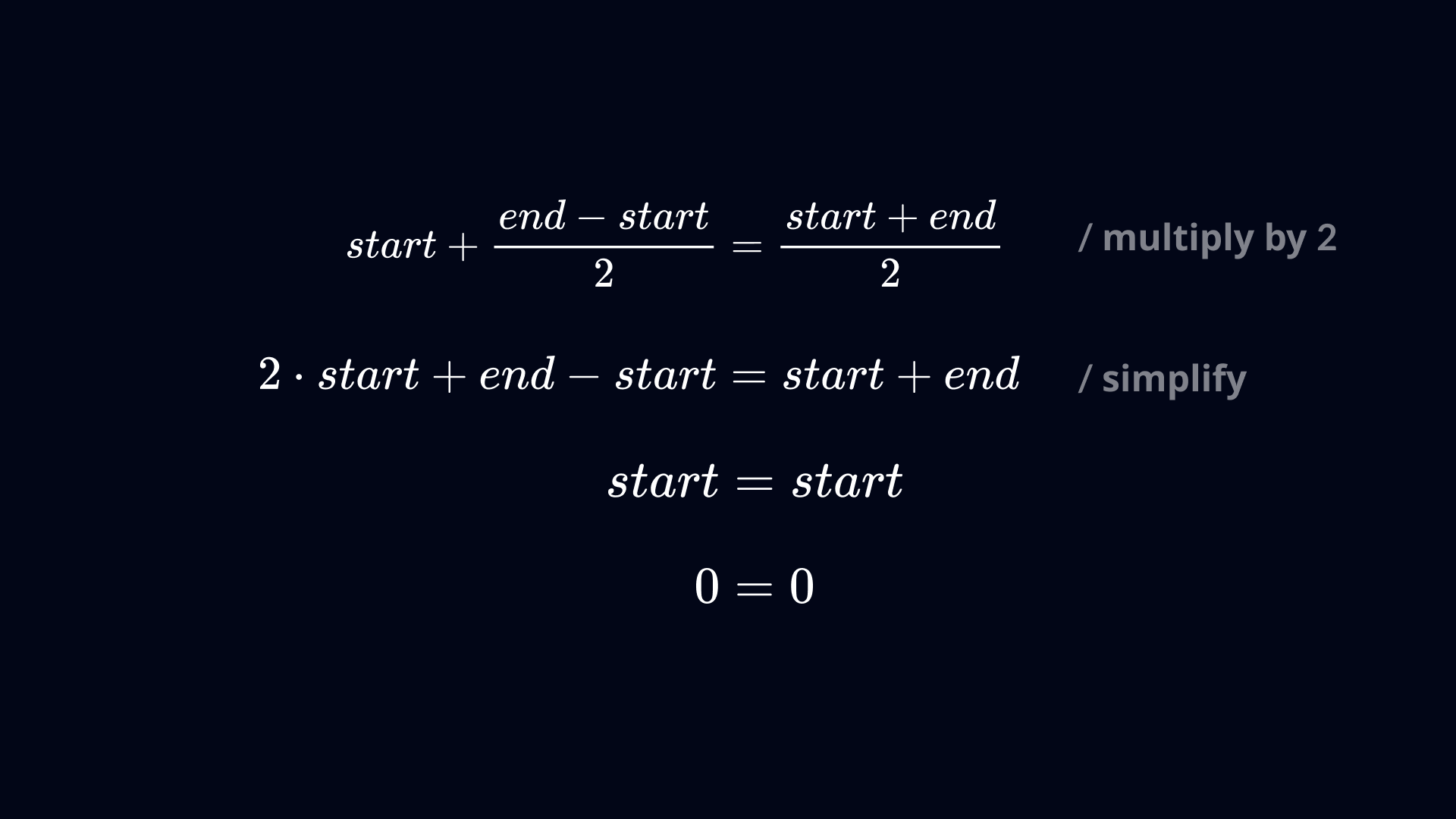
Ok, both methods produce the same value. And although this "correct" method isn't as straightforward, it actually ensures that any result of the intermediate calculation isn't larger than the value of end, thus preventing overflow. Computerphile made a very nice visual representation of this in their video about Binary Search. Here is my recreation of it, comparing the two methods of finding the middle index:

middle = (start + end) / 2

middle = start + (end - start) / 2

A well-hidden bug

If there's anything that made me feel a bit better after discovering that my code contains a (potentially disastrous) bug, is the fact that I'm not alone. Many far more experienced programmers missed this bug as well and even Java's own Binary Search in java.util.Arrays contained this bug until it was fixed in 2006!

The Hidden Bug in Binary Search