LeetCode #2392 Build a Matrix With Conditions, Topological Sort and Kahn's Algorithm

You are given a positive integer k. You are also given:

• a 2D integer array rowConditions of size n where rowConditions[i] = [above<sub>i</sub>, below<sub>i</sub>], and

• a 2D integer array colConditions of size m where colConditions[i] = [left<sub>i</sub>, right<sub>i</sub>].

The two arrays contain integers from 1 to k.

You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.

The matrix should also satisfy the following conditions:

• The number above<sub>i</sub> should appear in a row that is strictly above the row at which the number below<sub>i</sub> appears for all i from 0 to n - 1.

• The number left<sub>i</sub> should appear in a column that is strictly left of the column at which the number right<sub>i</sub> appears for all i from 0 to m - 1.

Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.

Let's look at Example 1: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]].

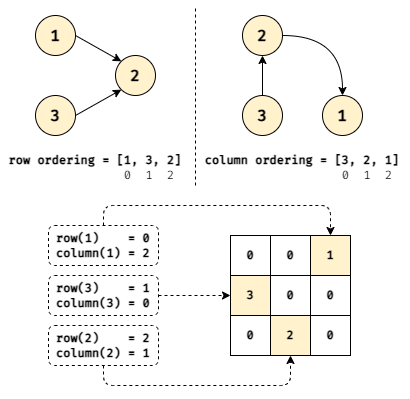
The rowConditions and colConditions forms a directed graph. If we found the ordering of numbers from rowConditions and colConditions, then we can find the positions of those number in matrix from that ordering.

To find such ordering in directed graph, first we need to make sure that the graph is acyclic, because there the ordering is not possible in cyclic graph. Then we can apply Topological Sort to find the topological ordering. There are different ways to apply topological sort - Kahn's Algorithm, Depth-First Search, etc.

Kahn's Algorithm

Kahn's algorithm works by repeatedly removing nodes with zero incoming edges until no nodes remains in a graph.

def topological_sort(edges: List[List[int]], num_nodes:int) -> List[int]:
        """Kahn's Algorithm"""

        graph = {node: [] for node in range(1, num_nodes + 1)}
        indegree = {node: 0 for node in range(1, num_nodes + 1)}
        for u, v in edges:
            graph[u].append(v)
            indegree[v] += 1

        queue = deque([])
        for node in indegree:
            if indegree[node] == 0:
                queue.append(node)

        order = []
        while queue:
            node = queue.popleft()
            order.append(node)
            for neighbor in graph.get(node, []):
                indegree[neighbor] = indegree.get(neighbor, 0) - 1
                if indegree[neighbor] == 0:
                    queue.append(neighbor)

        if len(order) != num_nodes:
            return []

        return order

The advantage of using Kahn's algorithm is that, it is able to detect cycle in the graph.
len(order) != num_nodes checks if all the nodes are included in topological ordering. If not, then there is a cycle.

Kahn's algorithm takes O(V + E) time - O(E) for computing in-degrees and O(V) for computing the order, and O(V) space, for storing intermediate nodes in a queue.

Now, let's get back to our problem. As previously said, we can find the positions of numbers in matrix by computing the ordering from rowConditions and colConditions.

class Solution:
    def buildMatrix(self, k: int, row_conditions: List[List[int]], col_conditions: List[List[int]]) -> List[List[int]]:

        def topological_sort(edges: List[List[int]], num_nodes:int) -> List[int]:
            """Kahn's Algorithm"""

            graph = {node: [] for node in range(1, num_nodes + 1)}
            indegree = {node: 0 for node in range(1, num_nodes + 1)}
            for u, v in edges:
                graph[u].append(v)
                indegree[v] += 1

            queue = deque([])
            for node in indegree:
                if indegree[node] == 0:
                    queue.append(node)

            order = []
            while queue:
                node = queue.popleft()
                order.append(node)
                for neighbor in graph.get(node, []):
                    indegree[neighbor] = indegree.get(neighbor, 0) - 1
                    if indegree[neighbor] == 0:
                        queue.append(neighbor)

            if len(order) != num_nodes:
                return []

            return order

        row_order = topological_sort(row_conditions, k)
        col_order = topological_sort(col_conditions, k)

        if not row_order or not col_order:
            return []

        val_indices = {}
        for i, v in enumerate(row_order):
            val_indices[v] = [i, None]
        for i, v in enumerate(col_order):
            val_indices[v][1] = i

        matrix = [[0 for _ in range(k)] for _ in range(k)]

        for val, (i, j) in val_indices.items():
            matrix[i][j] = val

        return matrix

Reference: Kahn's Algorithm.