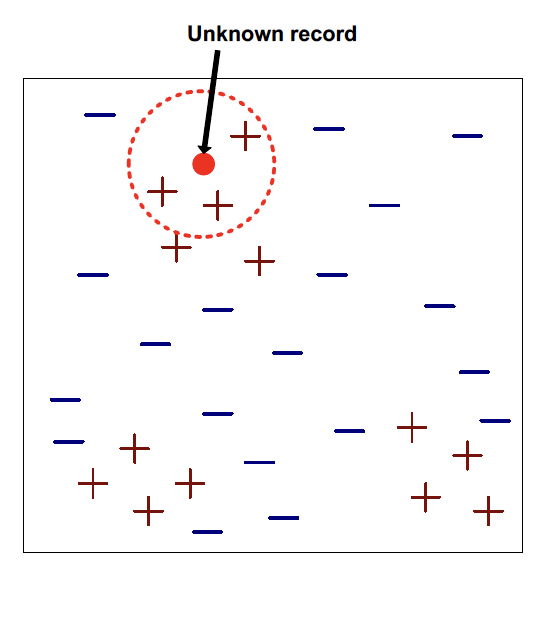
Introduction

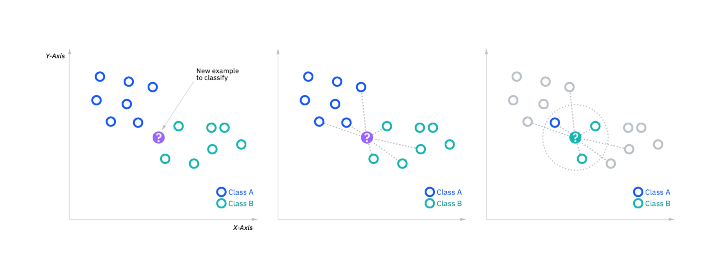
K-Nearest Neighbors (KNN) is an intuitive algorithm used for classification and regression. Imagine you move to a new neighborhood and want to know the best restaurant. You ask your closest neighbors for recommendations, and the majority vote wins. KNN works similarly but with data points.

How Does KNN Work?

Let's break down the steps involved in the KNN algorithm:

Choose the number of neighbors (k): The algorithm considers the 'k' closest data points (neighbors) to make a prediction.
Calculate the distance: The distance to all other data points is calculated for each data point. Common metrics include Euclidean Distance, Manhattan Distance, and Minkowski Distance.
Sort the distances: Sort these distances in ascending order and select the nearest 'k' neighbors.
Vote for the classes: The majority class among the neighbors determines the predicted class for classification. For regression, the average value of the neighbors is taken.
Assign the class or value: The class or value determined by the neighbors is assigned to the data point.

Importance of Weighted KNN

Sometimes, it's better to give more importance to closer neighbors than those farther away. Weighted KNN assigns weights to neighbors based on their distance: closer neighbors have higher weights. This can improve the accuracy of the predictions, especially when data points are unevenly distributed.

Implementing the weighted KNN in Python

Initialize Prediction List variable:
```
 y_pred = []
```
This list will store the predicted class for each test instance.
Iterate over each test Instance:
```
 for x in X_test:
```
Loop through all test data points.
Calculate Distances:
```
 distances = [np.sqrt(np.sum((x - x_train) ** 2)) for x_train in self.X_train]
```
Compute the Euclidean distance between the test instance and all training instances.
Sort Distances and Select Nearest Neighbors:
```
 sorted_distances = np.argsort(distances)
 neighbors_elements = sorted_distances[:self.k]
```
Sort distances and pick the indices of the 'k' nearest neighbors.
Compute weights:
```
 weights = [1 / (distances[i] + 1e-5) for i in neighbors_elements]
```
Assign weights to each neighbor based on their distance (closer neighbors get higher weights).
Perform weighted vote:
```
 weighted_votes = np.bincount(nearest_labels, weights=weights)
```
Use np.bincount to perform a weighted vote where closer neighbors have more influence.
Assign the class or value:
```
 predicted_label = weighted_votes.argmax()
```
The class with the highest weighted vote is chosen as the predicted class.

Code

import numpy as np
def KNN(X_train, y_train, X_test, k):
    """
    Predict the class labels for the provided test data using the K-Nearest Neighbors algorithm.

    Parameters:
    X_train (numpy.ndarray): Training data points.
    y_train (numpy.ndarray): Labels corresponding to the training data.
    X_test (numpy.ndarray): Test data points for which the predictions are to be made.
    k (int): Number of nearest neighbors to consider.

    Returns:
    numpy.ndarray: Predicted class labels for the test data points.
    """
    y_pred = []

    for x in X_test:
        # Calculate the Euclidean distance from the test point to all training points
        distances = [np.sqrt(np.sum((x - x_train) ** 2)) for x_train in X_train]

        # Sort the distances and get the indices of the k nearest neighbors
        sorted_distances = np.argsort(distances)
        neighbors_elements = sorted_distances[:k]

        # Retrieve the labels of the k nearest neighbors
        nearest_labels = [y_train[i] for i in neighbors_elements]

        # Compute the weights for each neighbor (inverse of distance)
        weights = [1 / (distances[i] + 1e-5) for i in neighbors_elements]

        # Perform a weighted vote for the nearest labels
        weighted_votes = np.bincount(nearest_labels, weights=weights)

        # Determine the predicted label as the one with the highest weighted vote
        predicted_label = weighted_votes.argmax()

        # Append the predicted label to the list of predictions
        y_pred.append(predicted_label)

    return np.array(y_pred)

Conclusion

K-Nearest Neighbors (KNN) is a simple yet powerful algorithm for classification and regression tasks. By understanding the importance of choosing the right number of neighbors (k) and incorporating weights, we can enhance the accuracy of our predictions. Visualizing the algorithm helps to see its impact and effectiveness in action.

This concludes the detailed explanation of the KNN algorithm and its implementation with weighted distances.

Understanding K-Nearest Neighbors (KNN): From Basics to Weighted KNN

Table of contents