Day 1: Linear Regression from Scratch

Ich versuche das Gelernte aus dem Online Coursera Kurs "Machine Learning Specialisation" von Andrew Ng gleich in die Praxis umzusetzen. Daher der Versuch Lineare Regression from Scratch zu implementieren. Los gehts.

# prompt: importiere numpy und eine mathematische zeichenbibliothek

import numpy as np
import matplotlib.pyplot as plt

Auf dem Weg versuche ich gleich mal, wie weit man mit Gemini als Codeing Assistant kommt.

x = np.array([1,2,3,4,5])
y = np.array([2,4,6,8,10])

# prompt: a function to plot the data x and y

def plot_data(x, y):
  """
  Plots the data points x and y.
  """
  plt.plot(x, y, 'o')
  plt.xlabel('x')
  plt.ylabel('y')
  plt.title('Data Plot')
  plt.show()

plot_data(x, y)

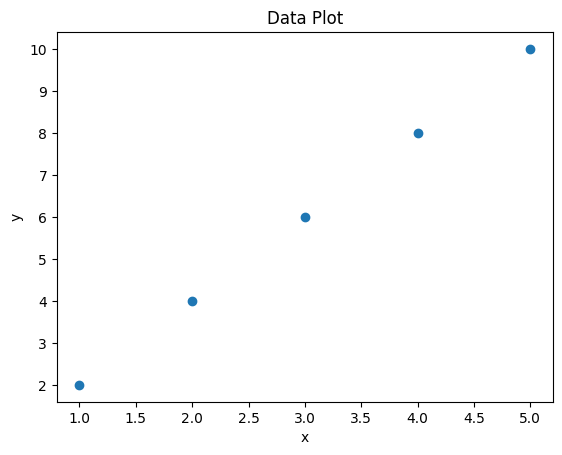
Ok. Das hat ja schonmal ganz gut geklappt. Schade nur, dass er den ganzen bisher geschriebenen Code nochmal ausgibt. Auch schade, dass man nicht innerhalb eines Codeblocks sich etwas einfügen lassen kann. Aber vllt. wird das ja in Zukunft noch verbessert. Weiter gehts. Wenn ich mich recht erinnere brauche ich jetzt ein w und ein b.

# prompt: ich brauche ein w und ein b um mit den zugehörigen x die erwarteten y zu berechnen

# Initialize w and b
w = 1  # Initial slope
b = 0  # Initial intercept

def compute_predictions(x, w, b):
  """
  Computes the predicted y values for the given x, w, and b.
  """
  y_predicted = w * x + b
  return y_predicted

# Example usage:
y_predicted = compute_predictions(x, w, b)
print(y_predicted)

[1 2 3 4 5]

Wow, das ist wirklich beeindruckend. Jetzt hat Gemini auch gar nicht den ganzen Code ausgegeben, sondern zwischendurch mit ... abgekürzt. Nun gut mal sehen, ob ich auch eine Funktion für die Kostenfunktion hinbekomme.

# prompt: ich brauche jetzt eine Funktion für die erste Ableitung der KostenFunktion für die  Lineare Regression

def compute_gradient(x, y, w, b):
  """
  Computes the gradient of the cost function for linear regression.

  Args:
    x (ndarray): Shape (m,)  input data
    y (ndarray): Shape (m,)  target values
    w (scalar):              current value of w
    b (scalar):              current value of b

  Returns:
    dj_dw (scalar): The gradient of the cost w.r.t. the parameter w
    dj_db (scalar): The gradient of the cost w.r.t. the parameter b
  """
  m = x.shape[0]
  dj_dw = 0
  dj_db = 0

  for i in range(m):
    err = (w * x[i] + b) - y[i]
    dj_dw += err * x[i]
    dj_db += err
  dj_dw = dj_dw / m
  dj_db = dj_db / m

  return dj_dw, dj_db

Wenn man genau sagt was man will, dann scheint das auch gut zu funktionieren. Interessanterweise hat er diesmal gar nicht mehr meinen alten Code zurückgegeben, sondern wirklich nur diese Funktion.

compute_gradient(x, y, w, b)

(-11.0, -3.0)

Mal sehen, ob ich mir ein Gradientenfeld für alle ganzzahligen w,b von -2 bis 2 anzeigen lassen kann.

# prompt: zeichne mir das gradientenfeld für alle ganzzahligen w und b von -2 bis 2

# Create grid of w and b values
w_vals = np.arange(-2, 3)
b_vals = np.arange(-2, 3)
W, B = np.meshgrid(w_vals, b_vals)

# Calculate gradients for each (w, b) pair
U = np.zeros_like(W)
V = np.zeros_like(B)
for i in range(W.shape[0]):
  for j in range(W.shape[1]):
    dj_dw, dj_db = compute_gradient(x, y, W[i, j], B[i, j])
    U[i, j] = dj_dw
    V[i, j] = dj_db

# Plot the gradient field
plt.figure(figsize=(8, 6))
plt.quiver(W, B, U, V, angles='xy', scale_units='xy', scale=1)
plt.xlabel('w')
plt.ylabel('b')
plt.title('Gradient Field')
plt.xlim([-2.5, 2.5])
plt.ylim([-2.5, 2.5])
plt.grid(True)
plt.show()

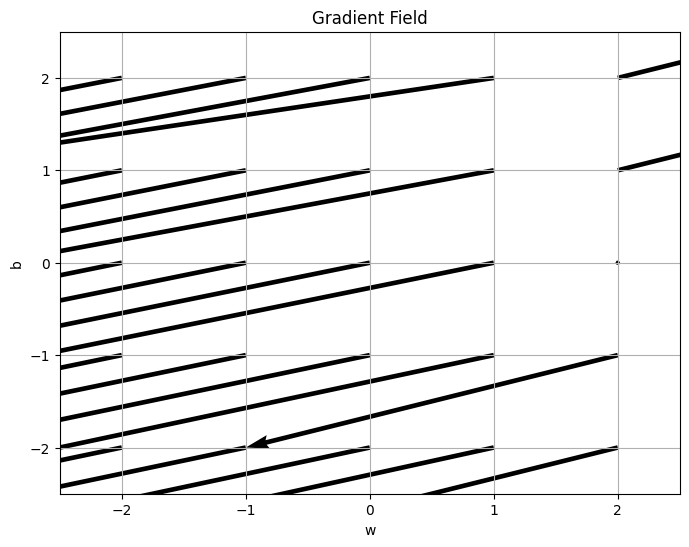
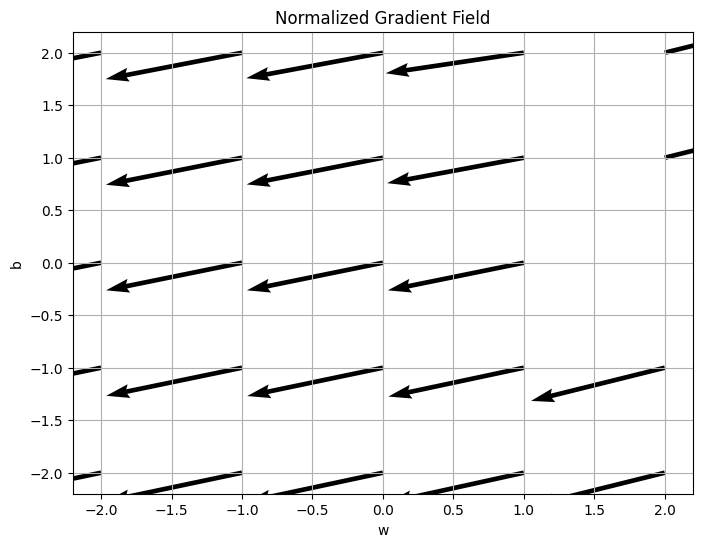
# prompt: ich bräuchte das gradientenfeld bitte normiert

# Normalize the gradient vectors
U_norm = U / np.sqrt(U**2 + V**2)
V_norm = V / np.sqrt(U**2 + V**2)

# Plot the normalized gradient field
plt.figure(figsize=(8, 6))
plt.quiver(W, B, U_norm, V_norm, angles='xy', scale_units='xy', scale=1)
plt.xlabel('w')
plt.ylabel('b')
plt.title('Normalized Gradient Field')
plt.grid(True)
plt.show()